离散型分布

发表于 分类于 ， 阅读次数： 本文字数： 5.1k 阅读时长 ≈ 5 分钟

本文讲了几个离散型分布，表示有限事件发生的概率，日常使用记住这 3 个即可伯努力分布 (2 点分布)、均匀分布、正太分布

  • 什么是单点分布?

    • 单点分布(one-point distribution)亦称一点分布，或称退化分布，是一种最简单的离散型分布

    • 假如随机变量 X 仅取数值 a，即 P{X=a}=1，则称随机变量 X 服从单点分布或退化分布

      P(x)={1,x=a0,x!=aP(x)= \begin{cases} {1}, & \text {x=a} \\ 0, & \text{x!=a} \end{cases}

    • 单点分布的均值E(x)=a，方差Var(x)=0

    • 该分布下数据恒等于a

  • 什么是伯努利分布(bernoulli)?

    • 又称两点分布( two-point distribution)或0-1分布，是一个离散型概率分布。在一次试验中，事件A出现的概率为P，事件A不出现的概率为q=1-p

      P(x)={p,x=aq,x=bP(x)= \begin{cases} p, & \text {x=a} \\ q, & \text{x=b} \end{cases}

    • 两点分布的均值 E(X)=pa+qbE(X)=pa+qb ,方差为V(X)=pq(a−b)2V(X)=pq(a-b)^2

    • 该分布下数据仅有两个可取值，且任意一次随机，取a或b的概率不变

  • 什么是均匀分布(uniform)？

    • 离散型均匀分布是一个离散型概率分布，其中有限个数值拥有相同的概率，典型的如抛硬币，掷色子，概率密度函数

      f(x)={1b−a,a< x < b 0,elsef(x)= \begin{cases} {\frac 1 {b-a}}, & \text {a< x < b } \\ 0, & \text{else}\end{cases}

    • 期望:E(X)=∫−∞∞xf(x)dx=∫abxb−adx=b−a2E(X)=\int_{-\infty}^{\infty} xf(x) dx=\int_{a}^{b} \frac{x}{b-a}dx=\frac{b-a} {2} 方差 V(X)=(b−a)212V(X)=\frac {(b-a)^2} {12}

    • 均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值

  • 什么是二项分布？

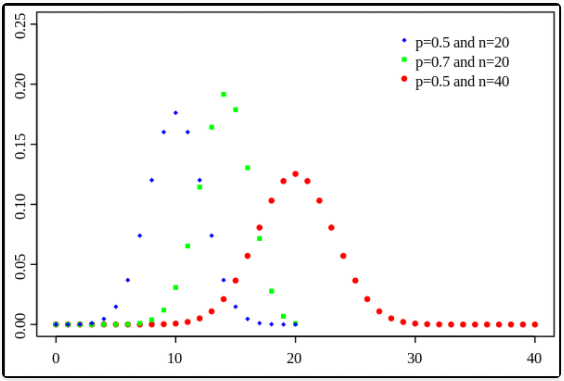
    • 在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验
    • 当n = 1时，又称伯努利分布(bernoulli)
    • n次试验中正好得到k次成功的概率：P(n,k,p)=Cnk∗pk(1−p)n−kP(n,k,p)=C^k_n*p^k(1-p)^{n-k} , 其中p称为成功概率，记作ξ~B(n,p)
    • 期望Eξ=npE\xi=np 方差：Dξ=np(1−p)D\xi=np(1-p)

  • 什么是多项分布(nultinomial distribution)？

    • k 面骰子滚动 n 次的每一面的计数概率建模。对于 n 个 独立试验，每个试验都导致 k 个 类别中的一个成功，每个类别具有给定的固定成功概率，多项式分布给出了各种类别成功数量的任何特定组合的概率，当K=2，n=1时，多项式分布为伯努利分布(bernoulli)，当k=2，n>1时为二项分布 ，当k>2,n=1时，为分类分布

    • 二项分布的典型例子是扔硬币，硬币正面朝上概率为p, 重复扔n次硬币，k次为正面的概率即为一个二项分布概率。把二项分布公式推广至多种状态，就得到了多项分布

    • 在N次独立实验中有mim_{i}次xi=1x_{i}=1的概率

      P(m1,…,md∣N,μ)=N!m1!…md!∏i=1dμimiP(m_1,…,m_d|N,\mu)=\frac{N!}{m_1!…m_d!}\prod_{i=1}^d\mu_i^{m_i}

    • 多项式分布与分类分布 (categotical distribution)的关系与伯努利分布(bernoulli)与二项分布的关系相同

  • 什么是分类分布 (categotical distribution)？

    • 又称多伯努利分布，是一种离散概率分布，它描述了一个随机变量的可能结果，该随机变量可以采用K 个可能的类别之一，其概率为每个类别的单独指定。这些结果没有先天的潜在排序，但为了方便描述分布，通常会附加数字标签（例如 1 到K）
    • 该ķ维类别分布是在最一般的分布K路事件；大小为K 的 样本空间上的任何其他离散分布都是特例。指定每个可能结果的概率的参数仅受以下事实的约束：每个参数必须在 0 到 1 的范围内，并且所有参数总和必须为 1
    • 交叉熵和采取负对数的多伯努利分布具有相同的形式

  • 什么是负二项分布？

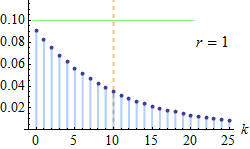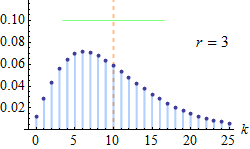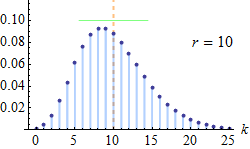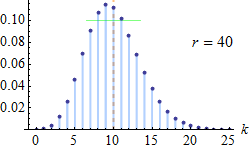
    • 负二项分布是统计学上一种描述在一系列独立同分布的伯努利试验中，失败次数到达指定次数（记为r）时成功的次数。比如，如果我们定义掷骰子随机变量x值为x=1时为失败，所有x≠1为成功，这时我们反复掷骰子直到1出现3次（失败次数r=3），此时非1数字出现次数的概率分布即为负二项分布

    • 随机变量X服从参数为r和p的负二项分布，则记为X~NB(r,p)

    • 当r是整数时，负二项分布又称帕斯卡分布（巴斯卡分布）

    • 概率密度函数 ：

      f(k;r,p)=Pr(x=k)=(k+r−1k)pk(1−p)r,k=0,1,2…(k+r−1k)=(k+r−1)!k!(r−1)!f(k;r,p)=Pr(x=k)= \begin{pmatrix} k+r-1 \\ k \\ \end{pmatrix}p^k(1-p)^r, \text {k=0,1,2…}\\ \begin{pmatrix} k+r-1 \\ k \\ \end{pmatrix}=\frac{(k+r-1)!}{k!(r-1)!}

    • 期望：E(X)=r(1−p)pE(X)=\frac{r(1-p)}{p} 方差：D(X)=r(1−p)p2D(X)=\frac{r(1-p)}{p^2}

  • 二项分布与负二项分布的区别?

    • “二项分布”是固定试验总次数N的独立试验中，成功次数k的分布；
    • “负二项分布”是所有到失败r次时即终止的独立试验中，成功次数k的分布

  • 什么是正态分布？

    • 又名高斯分布（Gaussian distribution），是一个非常常见的连续概率分布。正态分布在统计学上十分重要，经常用在自然和社会科学来代表一个不明的随机变量
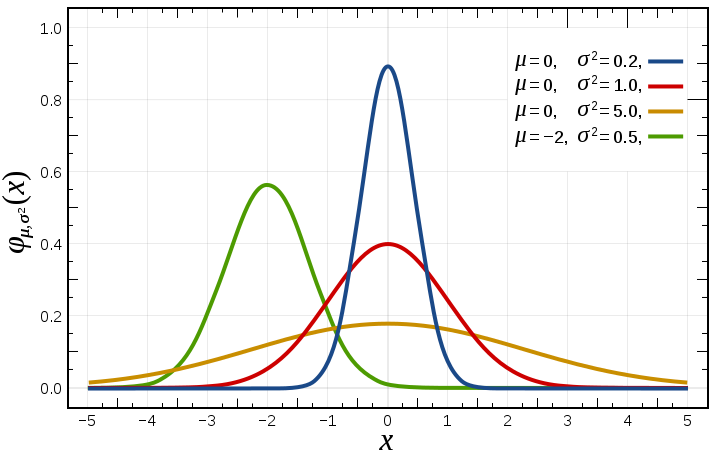
    • 若随机变量 X 服从一个位置参数为 μ、尺度参数为 σ 的正态分布，记为X−N(μ,σ2)X-N(μ,σ^2) ，概率密度函数(概率密度)：f(x)=1σ2πe−(x−μ)22σ2f(x)=\frac{1}{σ \sqrt {2\pi} }e^{- \frac{(x-μ)^2}{2σ^2}}
    • 其中期望：μμ 方差：σ2σ^2 ，其中μ决定了分布的横轴位置；其方差 σ2σ^2 决定了分布的幅度，标准正态分布是位置参数 μ =0，尺度参数 σ2σ^2 = 1的正态分布
    • 在特定条件下，大量统计独立的随机变量的平均值的分布趋于正态分布，这就是中心极限定理
    • 约68.3%数值分布在距离平均值有1个标准差之内的范围，约95.4%数值分布在距离平均值有2个标准差之内的范围，以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”

  • 何时采用正态分布?

    • 缺乏实数上分布的先验知识, 不知选择何种形式时, 默认选择正态分布总是不会错的, 理由如下
    • 中心极限定理告诉我们, 很多独立随机变量均近似服从正态分布, 现实中很多复杂系统都可以被建模成正态分布的噪声, 即使该系统可以被结构化分解
    • 正态分布是具有相同方差的所有概率分布中, 不确定性最大的分布, 换句话说, 正态分布是对模型加入先验知识最少的分布

  • 什么是几何分布？

    • 几何分布（eometric distribution）指的是以下两种离散型概率分布中的一种
      1
      2
      在伯努利试验中，得到一次成功所需要的试验次数X。X的值域是{ 1, 2, 3, ... }
      在得到第一次成功之前所经历的失败次数Y = X − 1。Y的值域是{ 0, 1, 2, 3, ... }
    • 如果每次试验的成功概率是p，那么k次试验中，第k次才得到成功的概率是

      Pr(X=k)=(1−p)k−1pPr(Y=k)=(1−p)kpPr(X=k)=(1-p)^{k-1}p\\ Pr(Y=k)=(1-p)^{k}p

  • 什么是超几何分布？

    • 超几何分布是统计学上一种离散概率分布。它描述了由有限个物件中抽出 n 个物件，成功抽出指定种类的物件的个数（不归还）, 例如在有 N 个样本，其中 m 个是不及格的。超几何分布描述了在该 N 个样本中抽出 n 个，其中 k 个是不及格的机率

      f(k;n,m,N)=CmkCN−mn−kCNnf(k;n,m,N)=\frac{C_m^k C_{N-m}^{n-k}}{C_N^n}

    • CNnC_N^n 表示所有在N个样本中抽出n个的方法数目。CmkC_m^k 表示在m个样本中，抽出k个的方法数目，即组合数，又称二项式系数。剩下来的样本都是及格的，而及格的样本有N-m个，剩下的抽法便有CN−mn−kC_{N-m}^{n-k} 种

    • 若n=1，超几何分布还原为伯努利分布,和二项分布不同的是，在超几何分布中，特别强调的是抽出的样品在下一次抽取前不再放回去，但是如果抽取的次数 n和总共样品数 N 相比很小（大约 n / N < 0.05，这时在计算上二项分布和超几何分布相互间则没有主要的区别，此时人们更愿意采用二项分布的方法，因为在数学计算上二项分布要简单一些

    • 容器中一共10个球，其中6个黑色，4个白色，一共抽5次（抽出的球不放回去），在这5个球中有3个黑球的概率是：f(k=3)=C63C10−65−3C105=0.476f(k=3)=\frac{C_6^3 C_{10-6}^{5-3}}{C_{10}^5}=0.476

    • 期望：nmN\frac {nm} N 方差：n(m/N)(1−mN)(N−n)N−1\frac{n(m/N)(1-\frac mN)(N-n)}{N-1}

  • 什么是泊松分布？

    • 泊松近似是二项分布的一种极限形式。其强调如下的试验前提：一次抽样的概率值 p 相对很小，而抽取次数 n 值又相对很大。因此泊松分布又被称之为罕有事件分布。泊松分布指出，如果随机一次试验出现的概率为 p，那么在 n 次试验中出现 k 次满足泊松分布
    • 泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等
    • 某工厂在生产零件时，每200个成品中会有1个次品，那么在100个零件中最多出现2个次品的概率按照泊松分布应该是 f(100,0,1200)+f(100,1,1200)+f(100,2,1200)=0.986f(100,0,\frac{1}{200})+f(100,1,\frac{1}{200})+f(100,2,\frac{1}{200})=0.986
    • 概率质量函数 ：P(X=k)=e−λλkk!P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}
    • 期望：λ\lambda 方差：λ\lambda