统计推断之参数估计

发表于 分类于 ， 阅读次数： 本文字数： 2.1k 阅读时长 ≈ 2 分钟

参数估计就是就是根据已观察到的试验去估计分布公式上的参数，常用的方法有极大似然函数

  • 什么是统计推断？

    • 通过样本推断总体的分布或者分布的数字特征

  • 什么是参数估计？

    • 参数是分布的参数，也就是已知一个总体的分布类型，但是对分布里面的参数不清楚，如泊松分布 P(λ)P(\lambda),正态分布的 N(μ,σ2)N(\mu,\sigma^2),这时候需要对这些未知参数进行估计
    • 估计方法：通过已经观察到的试验对参数进行估计，常用的估计手段有极大似然估计、极大后验概率估计

  • 什么是点估计？

    • 以某个适当的统计量的估测值作为未知参数的估计值

  • 什么是矩估计？

    • 矩估计法是用样本n阶矩去估计总体n阶矩，n的大小由未知参数决定，在估计的过程中，解得未知参数
    • 矩估计的方法依赖于抽取的样本，不同的样本对应不同的参数估计值，所以具有一定随意性
    • 使用矩估计要求总体存在原点矩，有些随机变量（如柯西分布）的原点矩不存在，因此无法使用矩估计
    • 例子1
    • 例子2

  • 什么是极大似然估计（MLE）？

    • 似然函数(likelihood function)定义：已知结果，对参数是某个值的可能性预测
    • 最大似然估计原理： 找到一组估计值，使得未知参数取该组估计值时，观察值以最大概率出现
    • 极大似然函数通常取对数将连乘变为累加，然后取负数将最大似然估计与最小损失函数对应起来

  • 什么是极大后验概率估计（MAP）？

    • 频率学派模型参数源自某种潜在分布，希望从数据中推知该分布。对于数据的观测方式不同或者假设不同，那么推知的该参数也会因此而存在差异。求解时，假设模型参数有了一个先验分布，不再一味地依赖数据样例（万一数据量少或者数据不靠谱呢）

  • 极大似然估计（MLE）与极大后验概率估计（MAP）的区别

    • 求解模型是，通常要求经验风险、结构风险同时最小化，实际上经验风险最小化等价于极大似然估计，结构风险最小化等价于最大后验概率估计
    • 二分类的逻辑回归，对参数的极大似然估计推导出损失函数
    • 概率矩阵分解，对参数的最大后验概率估计推导出损失函数

  • 估计量的评选标准？

    • 无偏性 假设每次抽样，对参数θ\theta 均有一个估计值，记为θ^(X1,X2,….,Xn)\hat\theta(X_1,X_2,….,X_n) ,若取所有估计值的期望是对参数的θ\theta 正确无偏估计，即E(θ^)=θE(\hat\theta)=\theta ,则θ^\hat\theta 为θ\theta 的无偏估计量
    • 有效性 多次抽样，使用不同的方法计算得到多组θ\theta 的估计量，这两组中较稳定的（即方差小）较其他组更为有效的估计。方差反映估计值在真实值附近更为“集中”
    • 一致性（相合性） 毫无疑问，抽取样本的容量越大，对未知参数的估计越接近真实值，估计量的这种性质称为一致性（相合性）
    • 相合估计量 设θ^=θ^(X1,X2,…,Xn)\hat\theta=\hat\theta(X_1,X_2,…,X_n) 为未知参数θ\theta 的估计量，若θ^\hat\theta 依概率收敛于θ\theta ,则对任意ω>0\omega>0 ,有limn→+∞P(∣θ^−θ∣<ω)=1或limn→+∞P(∣θ^−θ∣>=ω)=0lim_{n \to +\infty}P(|\hat\theta-\theta|<\omega)=1 或 lim_{n \to +\infty}P(|\hat\theta-\theta|>=\omega)=0 ，此时，称θ^\hat\theta 为θ\theta (弱)相合估计量
    • 一般而言，三个估计量评选标准只要满足前面两个标准就不错了，因为使用一致性要求样本容量足够大

  • 什么是区间估计？

    • 用两个统计量的观测值确定的区间来估计未知参数的大致范围,并给出未知参数落在此区间的概率
    • 对于事先指定的概率1−α1-\alpha ,若有对未知参数θ\theta 的统计量θ1\theta_1 和θ2\theta_2 ，使得P(θ1≤θ≤θ2)=1−αP(\theta_1 \leq \theta \leq \theta_2)=1-\alpha ，那么(θ1,θ2)(\theta_1,\theta_2) 为θ\theta 置信水平为1−α1-\alpha 的置信区间，在θ1\theta_1 和θ2\theta_2 为置信上下限，在θ1−θ2\theta_1-\theta_2 为置信区间长度

  • 单正态总体参数的区间估计？

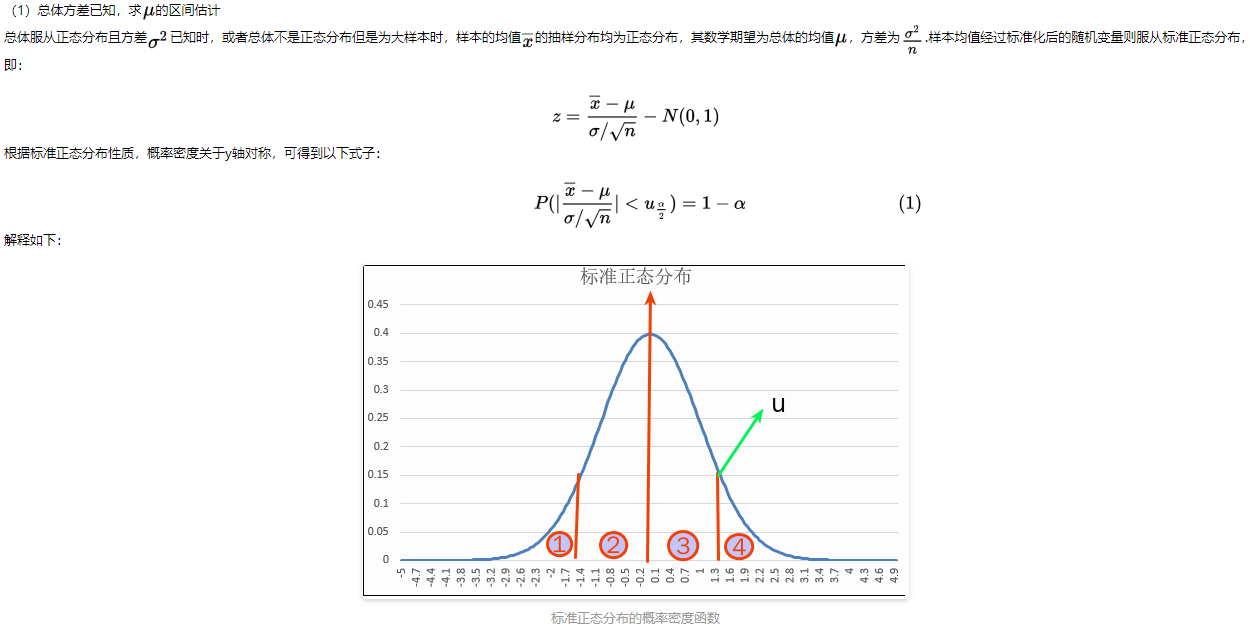
    • 均值区间估计
    • 总体方差未知，求μ\mu的区间估计

  • 双正态总体参数的区间估计？

    • 多因素引发质量指标X的变化，若X服从正态分布，则需要对两个正态分布的总体的均值差或方差比给出区间估计
    • 双正态总体均值差的区间估计
    • 双正态总体方差比的区间估计

  • (0-1)分布参数的区间估计 ？

  • 什么是无偏估计？

    • 所谓无偏，就是我们认为每个样本点出现的概率和真实模拟的数据中样本点出现的概率是一样的。当概率相等即无偏时，我们认为两者等价