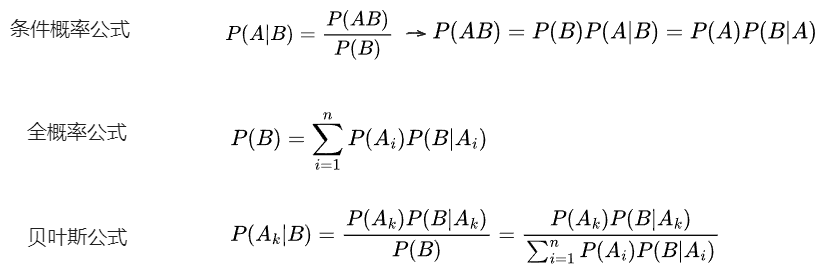概率论常见名词
本文分为两部分,第一部分先从随机变量讲起,然后讲解概率分布、概率质量、概率密度函数,尤其需要把握的是先验概率、后验概率、条件概率、全概率以及贝叶斯定理。第二部分讲解随机变量距离的计算方式
什么是概率论?
- 概率论是在给定条件(已知模型和参数)下,对要发生的事件(新输入数据)的预测
- 概率论是统计学的数学基础,统计学是对概率论的应用
什么是统计学?
- 统计推断是在给定数据(训练数据)下,对数据生成方式(模型和参数)的归纳总结
- 概率论是统计学的数学基础,统计学是对概率论的应用
机器学习为什么要使用概率?
- 事件的概率是衡量该事件发生的可能性的量度。虽然在一次随机试验中某个事件的发生是带有偶然性的,但那些可在相同条件下大量重复的随机试验却往往呈现出明显的数量规律
- 机器学习除了处理不确定量,也需处理随机量。不确定性和随机性可能来自多个方面,使用概率论来量化不确定性
- 概率论在机器学习中扮演着一个核心角色,因为机器学习算法的设计通常依赖于对数据的概率假设
什么是随机变量?
- 在客观世界中,存在大量的随机现象,随机现象产生的结果构成了随机事件。用变量来描述随机现象的各个结果,就叫做随机变量
- 随机变量有有限和无限的区分,一般又根据变量的取值情况分成离散型随机变量和连续型随机变量
随机变量的独立性?
- 两事件 X 和 Y 在给定的另一事件 Y 发生时条件独立,类似于统计独立性,就是指当事件 Z 发生时,X 发生与否和 Y 发生与否就条件概率分布而言是独立的
随机变量与变量的区别?
- 随机变量(random variable): 表示随机现象(在一定条件下,并不总是出现相同结果的现象称为随机现象)中各种结果的实值函数(一切可能的样本点)。例如某一时间内公共汽车站等车乘客人数,电话交换台在一定时间内收到的呼叫次数等,都是随机变量的实例
- 变量的取值的概率不是 1 时,变量就变成了随机变量;当随机变量取值的概率为 1 时,随机变量就变成了变量
什么是离散型随机变量?
- 有些随机变量,它全部可能取到的不相同的值是有限个或可列无限多个,也可以说概率以一定的规律分布在各个可能值上。这种随机变量称为 "离散型随机变量",如 抛硬币、掷色子、商品出现次品的个数
什么是连续型随机变量?
- 包括但不等于连续型随机变量, 连续型随机变量是指如果随机变量 X 的所有可能取值不可以逐个列举出来,而是取数轴上某一区间内的任一点的随机变量,如某一天的温度、某商品的寿命
什么是概率函数 (probability function) ?
用函数的形式来表达概率(一次只能表示一个取值的概率),比如可以用以下函数表示 "抛硬币出现点数" 事件的概率
该词和概率分布函数是同义词,所以这样理解是对的,可参下面的概率分布函数
随机变量与概率分布的联系?
- 一个随机变量仅仅表示一个可能取得的状态,还必须给定与之相伴的概率分布来制定每个状态的可能性。用来描述随机变量或一簇随机变量的每一个可能的状态的可能性大小的方法,就是概率分布 (probability distribution)
- 随机变量可以分为离散型随机变量和连续型随机变量
- 概率质量函数 (Probability Mass Function, PMF): 描述离散型随机变量的概率分布,通常用大写字母 表示
- 概率密度函数 (概率密度)(Probability Density Function, PDF): 描述连续型随机变量的概率分布,通常用小写字母 表示
什么是分布函数?
- 假设用 X 表示随机事件的概率,那么对于所有区间的概率均可以用 {X<=x} 来表示,如 {X>x}~1-{X<=x} ;
- 设 X 是随机变量,对于任意实数 x,则函数称为随机变量 X 的分布函数
- 离散型的随机变量与阶梯型的分布函数对应,连续型的随机变量与绝对连续型的分布函数对应
什么是概率质量函数?
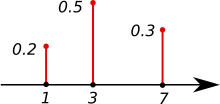
- 离散型随机变量在各特定取值上的概率,有时它也被称为离散密度函数
- 一个概率质量函数的图像。函数的所有值必须非负,且总和为 1
![]()
什么是概率密度函数 (概率密度)?
简称概率密度或密度函数,是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数,当概率密度函数存在的时候,累积分布函数是概率密度函数的积分
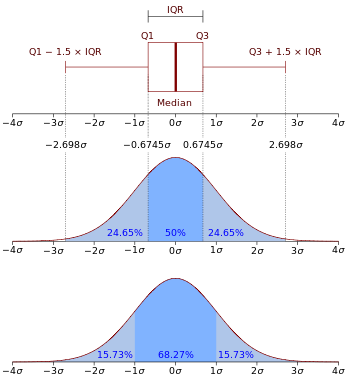
图中,横轴为随机变量的取值,纵轴为概率密度函数的值,而随机变量的取值落在某个区域内的概率为概率密度函数在这个区域上的积分,即随机变量 X 的分布函数 F (x),若存在一个非负函数 f (x),使得对于任意实数 x,有
以盒状图与概率密度函数展示的正态分布 N (0, σ2)
![]()
什么是概率分布函数及分布律?
- 设离散型随机变量 X 取值为 xi (i=1,2,3,….),且各个取值的概率是 , 上式为离散型随机变量 X 的概率分布或分布律
- 分布律与分布函数:
概率质量函数与概率密度函数的区别?
- 概率质量函数是对离散随机变量定义的,本身代表该值的概率;
- 概率密度函数 (概率密度) 函数本身不是概率,只有对连续随机变量的概率密度函数必须在某一个区间内被积分后才能产生出概率
分布函数与概率密度函数的关系?
- f (x) 本身不是概率,其大小决定了 X 落在区间上的概率,即 f (x) 反映了点 x 附近分布的概率 疏密 程度 (即概率密度)
- 当 很小时,
概率函数、分布函数、概率密度的关系?
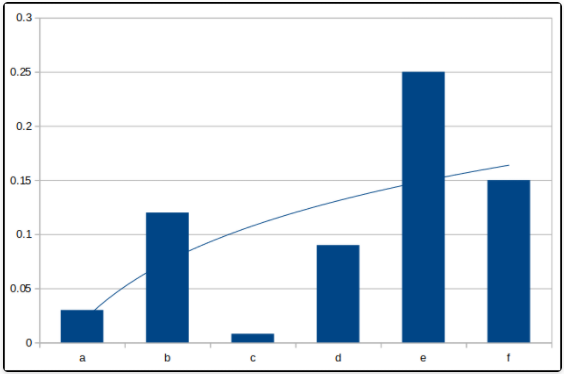
- 假设随机变量包含以下取值 {a,b,c,d,e,f}. 并假设其概率情况如下
![]()
- 概率函数:某个随机变量出现的概率,比如 a 出现的概率 P (X=a)=0.03
- 分布函数:一组随机变量出现的概率,比如 b,c,d 出现的概率 P (X={b,c,d})=0.218
- 概率密度函数 (概率密度): 连续型随机变量由于其变量的无穷,求概率时会引入积分概念
![]()
什么是累积分布函数?
- 随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分
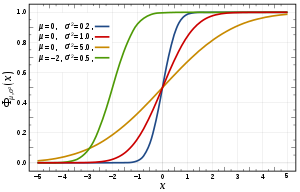
- 正态分布的累积分布函数
![]()
什么是先验概率?
- P (A) 是 A 发生的概率; 也叫作 A 的先验概率,是在 B 事件发生之前,对 A 事件概率的一个判断
什么是后验概率?
- P (A|B) 是在 B 发生的情况下 A 发生的概率; 也叫作 A 的后验概率,是在 B 事件发生之后,对 A 事件概率的重新评估
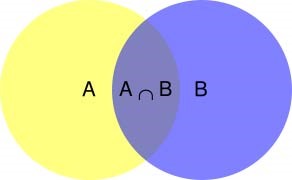
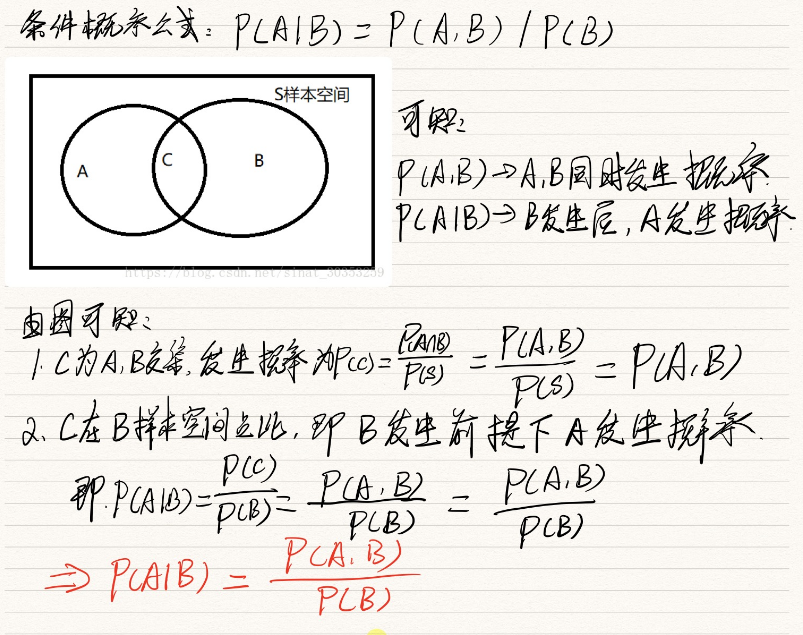
什么是条件概率?
![]()
- 条件概率是给定另一事件发生的一个(或多个)事件的概率,换句话说,它是当次要事件 B 为真时事件 A 发生的概
![]()
- 例子: 一对夫妻有两个小孩,已知其中一个是女孩,则另一个是女孩子的概率是多少?
- 穷举法:已知其中一个是女孩,那么样本空间为男女,女女,女男,则另外一个仍然是女生的概率就是 1/3
- 条件概率法:P (女 | 女)=P (女女)/P (女), 夫妻有两个小孩,那么它的样本空间为女女,男女,女男,男男,则 P (女女) 为 1/4,P(女)= 1-P (男男)=3/4, 所以最后 1/3
- 这里大家可能会误解,男女和女男是同一种情况,但实际上类似姐弟和兄妹是不同情况
条件概率的链式法则?
- 由条件概率的定义,可直接得出下面的乘法公式: 设 A, B 是两个事件,并且 P (A) > 0, 则有 ,推广得
- 一般地,用归纳法可证:若 P (A_1A_2…A_n)>0,则有
- 任何多维随机变量联合概率分布,都可以分解成只有一个变量的条件概率相乘形式
什么是联合概率?
- 联合概率是两个不同事件同时发生的概率,即两个(或更多)同时发生的事件,例如 P(A 和 B)或 P(A,B)
- 设 X 和 Y 都是离散型随机变量, 和 分别是 X 和 Y 的一切可能的几何,则 X 和 Y 的联合概率分布可以表示为
- 变量 X 和 Y 的联合分布完全决定 X 的概率分布和 Y 的概率分布 (边缘概率)
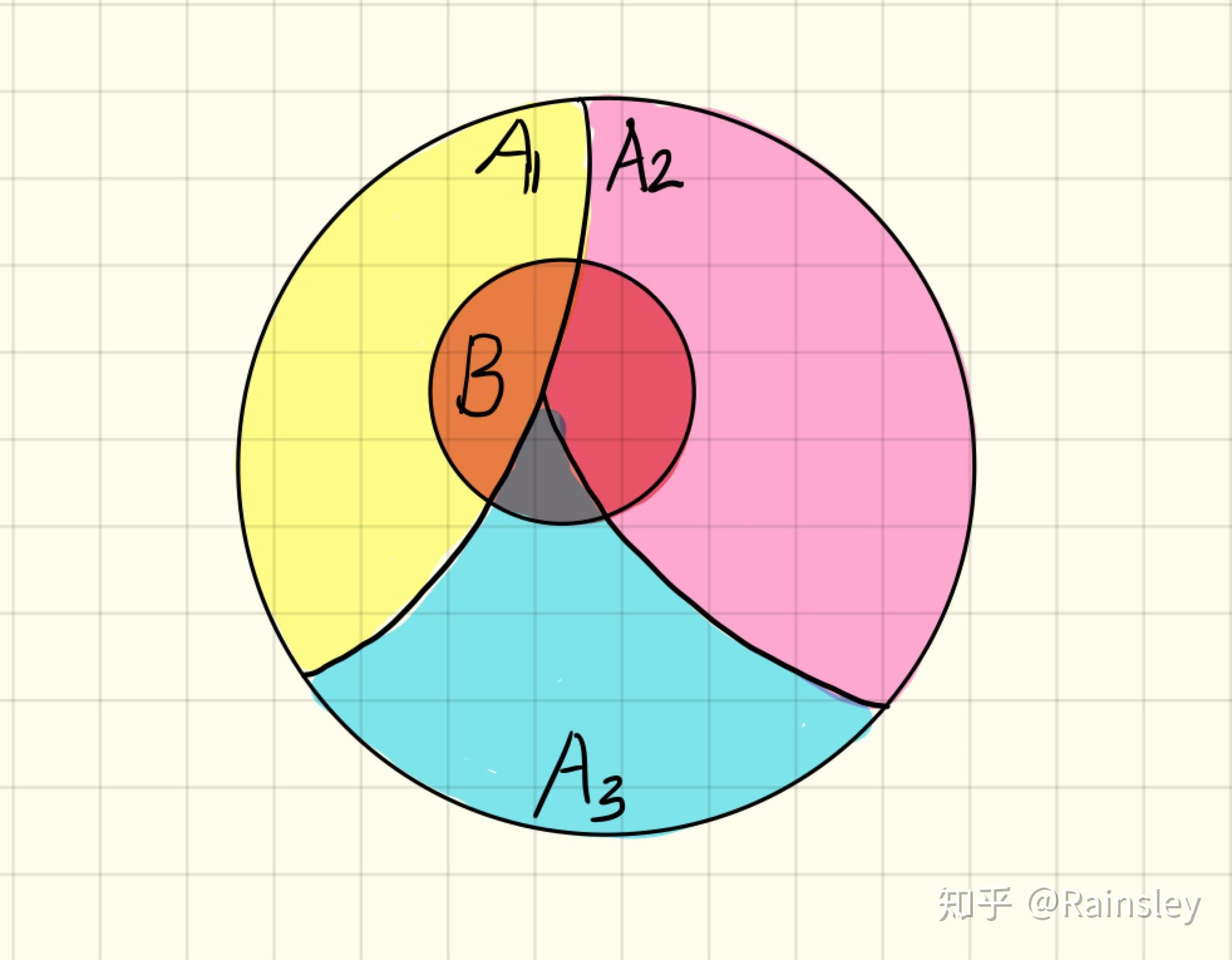
什么是全概率公式?
![]()
有时候直接计算某个事件 B 的概率比价困难,但是可以通过与事件 B 共同出现的情况,去预估 B 的概率。当 A 是一个完备事件时,有
例子
![]()
什么是贝叶斯定理?
- 是概率论中的一个定理,描述在已知一些条件下,某事件的发生概率,即关于随机事件 Y 和 X 的条件概率,其中,A、B 为随机事件,且 不为 0, 是指在事件 A 发生的情况下事件 B 发生的概率
- 先验概率 -> 后验概率: 是 B 的后验概率; 为 A、B 的先验概率,也就是所谓的经验,即不断使用时延修正后验概率,使得结果更加准确
- 后验概率 = 标准似然度 x 先验概率 : 是已知 A 发生的情况下,B 的条件概率,也叫特定 A 时,B 的似然性, 也被称作标准似然度。 意味着 "先验概率" 被增强,事件 A 的发生的可能性变大; 意味着 X 事件无助于判断事件 Y 的可能性;如果 ,意味着 "先验概率" 被削弱,事件 Y 的可能性变小
- 通俗理解地讲就是当你不能确定某一个事件发生的概率时,你可以依靠与该事件本质属性相关的事件发生的概率去推测该事件发生的概率。用数学语言表达就是:支持某项属性的事件发生得愈多,则该事件发生的的可能性就愈大。这个推理过程有时候也叫贝叶斯推理
- 例子
![]()
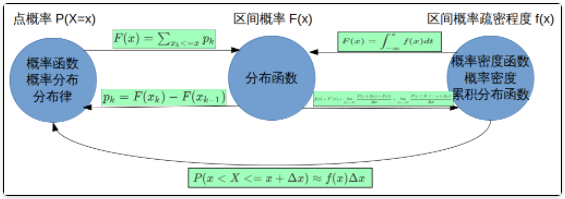
条件概率、全概率、贝叶斯公式的关系?
![Drawing 2023-10-11-21.14.24.excalidraw]()
- 条件概率与贝叶斯公式形式一样,贝叶斯公式考虑多事件情况而已
- 全概率公式作为贝叶斯公式的分母部分
什么是数学期望?
- 试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小
- 离散函数:
- 连续函数:
- 如果 X 和 Y 相互独立,则 $E (xy)=E (x) E (y) $
- 期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里
- 大数定律规定,随着重复次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值
什么是方差?
- 概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。方差是一种特殊的期望
- 常数的方差为 0
- 如果 X 和 Y 相互独立,
什么是协方差?
- 协方差是衡量两个变量线性相关性强度及变量尺度,包括同方向变化?还是反方向变化?同向或反向程度如何?
- 同向变化的,这时协方差就是正的,反向变化的,这时协方差就是负的
- 从数值来看,协方差的数值越大,两个变量同向程度也就越大
- 方差是一种特殊的协方差。当 X=Y 时,
- 独立变量的协方差为 0
什么是矩?
- 矩就是观察与描述随机变量的工具,不同的矩就是不同的维度
- 直接使用变量计算的矩被称为原始矩(raw moment),移除均值后计算的矩被称为中心矩(central moment)
- 零阶矩:所有变量取值的总概率(即 1)
- 一阶矩原点矩:期望,表示分布中心
- 二阶矩中心矩:随机变量的方差
- 三阶矩中心矩: 随机变量的偏态(衡量分布不对称性)
- 四阶矩中心矩:峰度, 一般随机变量的峰度定义为其四阶中心矩与方差平方的比值再减 3,减 3 是为了让正态分布峰度为 0
- 混合矩: 多个变量的矩,比如协方差,协偏度,协峰度。虽然协方差只有一个,但协偏度和协峰度存在多个
什么是协方差矩阵?
- n 维随机变量之间的协方差值,为了方便,用矩阵来组织这些数据,也就是协方差矩阵来
什么是相关系数?
- 描述两个随机变量线性相关程度的量,包括同方向变化?还是反方向变化?同向或反向程度如何?,D (x),D (y) 为两个随机变量的方差
- 越接近 1,表明正相关越强,越接近 - 1,表明负相关越强,越接近 0,表明相关性不强
- 有界性。相关系数的取值范围是 [-1,1],可以看成无量纲的协方差
- 值越接近 1,说明两个变量正相关性(线性)越强。越接近 - 1,说明负相关性越强,当为 0 时,表示两个变量没有相关性
协方差与相关系数的关系?
- 相关系数不像协方差一样可以在 到 间变化,它只能在+1 到-1 之间变化
- 相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差
什么是皮尔逊相关系数?
- 又称皮尔逊积矩相关系数(Pearson product-moment correlation coefficient,简称 PPMCC 或 PCCs),是用于度量两个变量 X 和 Y 之间的相关(线性相关),其值介于 - 1 与 1 之间
- 用协方差除以两个变量的标准差得到的,虽然协方差能反映两个随机变量的相关程度(协方差大于 0 的时候表示两者正相关,小于 0 的时候表示两者负相关)
什么是独立事件?
- 考虑两个事件 A 和 B。当事件 A 的发生概率不依赖于事件 B 的发生时,则 A 和 B 是独立的事件
什么是独立同分布 (independently and identically distributed)?
- 即监督学习假设输入与输出的随机变量 X 和 Y 都遵循联合概率分布 P (X,Y)
- 例如,某个网页的访问者在短时间内的分布,即分布在该短时间内没有变化,且一位用户的访问行为通常与另一位用户的访问行为无关。不过,如果将时间窗口扩大,网页访问者的分布可能呈现出季节性变化
什么是似然函数 (likelihood function)?
- 一种关于统计模型中的参数的函数,表示模型参数中的似然性
- 概率,用于在已知一些参数的情况下,预测接下来在观测上所得到的结果;似然性,则是用于在已知某些观测所得到的结果时,对有关事物之性质的参数进行估值,也就是说已观察到某事件后,对相关参数进行猜测
1
2概率:参数 + 观测 --> 结果
似然:观测 + 结果 --> 参数 - 极大似然估计 (MLE) 是似然函数最初也是最自然的应用,因为似然函数取得最大值表示相应的参数能够使得统计模型最为合理
概率函数、似然函数与参数估计的差别?
- 假如有一个函数, 其中 θ 是需要估计的参数,x 是具体的数据也就是样本
- 频率学派认为:存在唯一真值 θ
- 贝叶斯学派认为: θ 是一个随机变量,符合一定的概率分布。即不认为模型的参数 θ 是一个确定的值,而是认为参数 θ 本身也服从某种潜在分布
- 在贝叶斯学派里有两大输入和一大输出,输入是先验 (prior) 和似然 (likelihood),输出是后验 (posterior) , 先验,即 θ,指的是在没有观测到任何数据时对 θ 的预先判断 ; 似然,即 p (x|θ) ,是假设 θ 已知后我们观察到的数据应该是什么样子的; 后验,即 p (θ|x) , 是最终的参数分布 。 即对事件进行建模的时候,先假设有一个预估(先验概率),然后根据观测数据,不断调整之前的预估
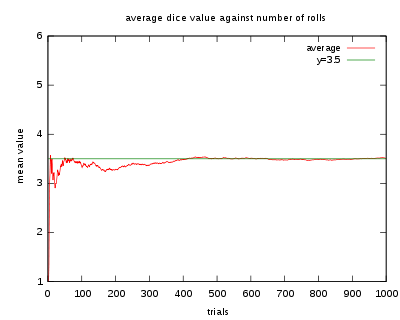
什么是大数定律?
- 在数学与统计学中,大数定律又称大数法则、大数律,是描述相当多次数重复实验的结果的定律。根据这个定律知道,样本数量越多,则其算术平均值就有越高的概率接近期望值
- 以特定掷单个骰子的过程来展示大数定律。随着投掷次数的增加,所有结果的均值趋于 3.5(骰子点数的期望值)。不同时候做的这个实验会在投掷次数较小的时候(左部)会表现出不同的形状,当次数变得很大(右部)的时候,它们将会非常相似
![]()
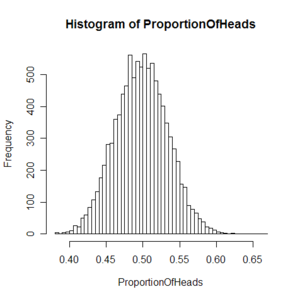
什么是中心极限定理?
- 中心极限定理是概率论中的一组定理。中心极限定理说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于标准正态分布
- 10,000 次抛掷硬币实验中出现正面的平均比率,每次抽樣(实验)的樣本數為 200(抛掷 200 次硬币)
![]()
参考: