DragDiffusion：Harnessing Diffusion Models for Interactive Point-based Image Editing

发表于 2023-11-03 更新于 2025-01-18 分类于 2-深度学习， B-视觉模型， 2-高级视觉任务GAN ，生成图片阅读次数：本文字数： 2.4k 阅读时长 ≈ 2 分钟

通过交互点控制图片生成
图 + 交互 -> 条件图片，图生图

什么是 DragDiffusion ？

借鉴 DragGAN，基于 DDPM 实现交互式的图像编辑功能
文章主要分为两部分：(1) LoRA 微调：通过 LoRA 和想要编辑的图像对 SD (StableDiffusion) 进行微调，保证在后面在对特征进行操作之后仍然能够保留图像信息；(2) 交互式图像编辑：借鉴 DragGAN 和运动监督、点跟踪两个过程，实现对图片的编辑

DragDiffusion 的原理？

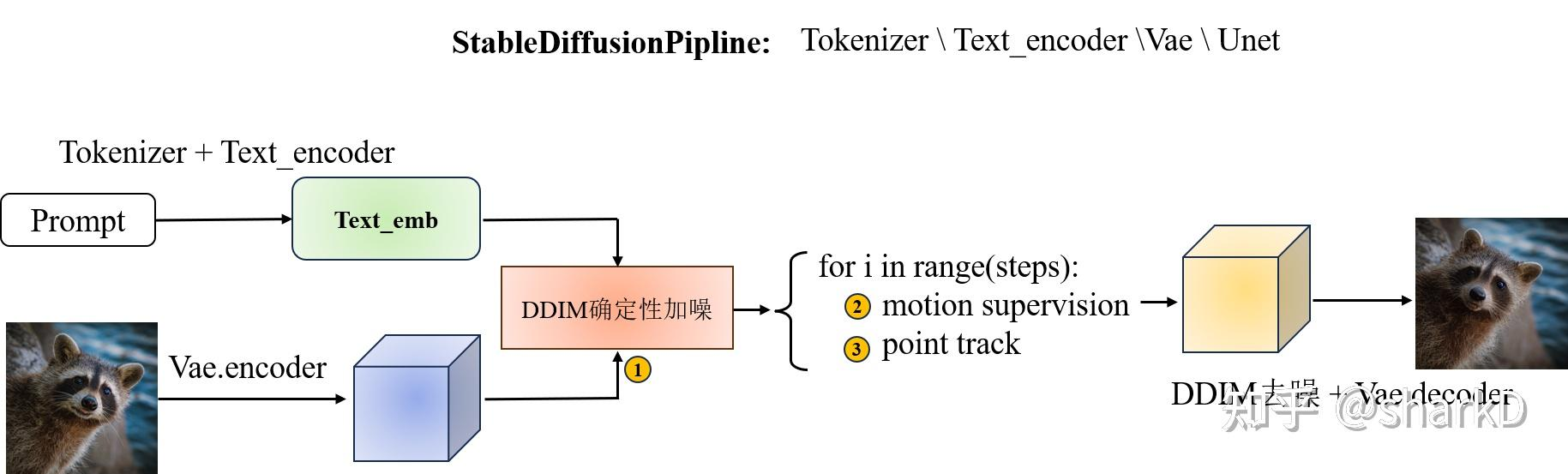
在交互信息的引导上，和 DragGAN 的运动监督、点跟踪过程一样，区别在于 DDPM 是在 VAE 的中间隐变量上学习，并且在 Unet 的倒数第二个 block 的特征图输入交互监督
运动监督：监督新生成的图像从起始点向目标点移动
点跟踪：获取移动后新的起始点，然后作为监督信息输入到下

DragDiffusion 如何进行运动监督？

运动监督和 DragGAN 一样，定义为中心的正方形块 $\Omega\left(h_i^k,r_1\right)=\left\{(x,y):\left|x-x_i^k\right|\leq r_1,\left|y-y_i^k\right|\leq r_1\right\}$ 为变长为 $2r_1+1$ ，以 $h_i^k=\left(x_i^k,y_i^k\right)$ 为中心的正方形块，则运动监督第 K 次的迭代优化目标

\begin{aligned}&\mathcal{L}\left(\hat{z}_{t}^{k}\right)=\sum_{i=1}^{n}\sum_{q\in\Omega\left(h_{i}^{k},r_{1}\right)}\left\|F_{q+d_{i}}\left(\hat{z}_{t}^{k}\right)-\mathrm{sg}\left(F_{q}\left(\hat{z}_{t}^{k}\right)\right)\right\|_{1} \\&\left.+\left.\lambda\right\|\left(\hat{z}_{t-1}^k-\operatorname{sg}(\hat{z}_{t-1}^0)\right)\odot(1-M)\right\|_1\end{aligned}

其中 $\hat{z_t^k}$ 是第 k 个运动监督之后的第 t 步扩散潜码， $d_i=\left(g_i-h_i^k\right)/\left\|g_i-h_i^k\right\|_2$ 是第 k 次迭代中从第 i 个控制点到第 i 个目标点的归一化方向量，M 是用户指定的二进制掩码，保证扩散潜码未被屏蔽的部分保持不变。当 $q+d_i$ 不是整数， $F_{q+d_i}\left(\hat{z}_t^k\right)$ 的值通过双线性插值计算。sg⁡(⋅) 是停止梯度操作，防止反向移动

DragDiffusion 如何进行点跟踪？

点跟踪和 DragGAN 一样，运动监督更新 $\hat{z}_t^k$ 后，控制点的位置也可能改变，所以需要进行点跟踪更新控制点。由于 UNet 特征可以很好的捕获点的响应，所以可以使用 $F\left(\hat{z}_{t}^{k+1}\right)$ 和 $F\left(\hat{z}_{t}^{k}\right)$ 来跟踪新的控制点
具体来说，在方块 $\Omega\left(h_{i}^{k},r_{1}\right)=\left\{(x,y):\left|x-x_{i}^{k}\right|\leq r_{2},\left|y-y_{i}^{k}\right|\leq r_{2}\right\}$ 内应用最近邻搜索来更新控制点 $h_i^{k}$ ，

h_i^{k+1}=\arg\min_{q\in\Omega\left(h_i^k,r_2\right)}\left\|F_q\left(\hat{z}_t^{k+1}\right)-F_{h_i^k}\left(z_t\right)\right\|_1

参考：