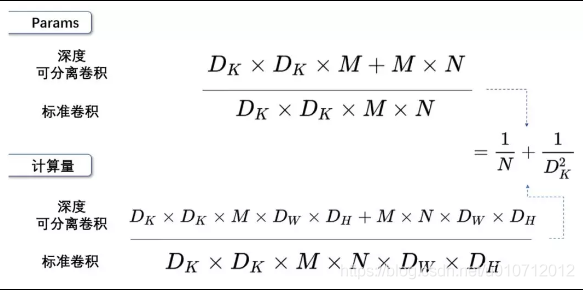卷积神经网络-CNN

发表于 2023-10-27 更新于 2023-10-30 分类于 2-深度学习， A-基础知识阅读次数：本文字数： 13k 阅读时长 ≈ 12 分钟

本文介绍 CNN 的基础原理，由此发展出多种概念，包括：1 x 1 卷积、分组卷积、空洞卷积、深度可分离卷积、分解卷积、反卷积、形变卷积等

什么是卷积 (Convolution)？

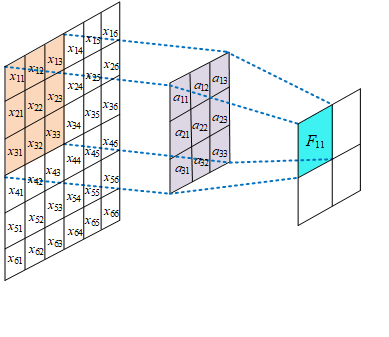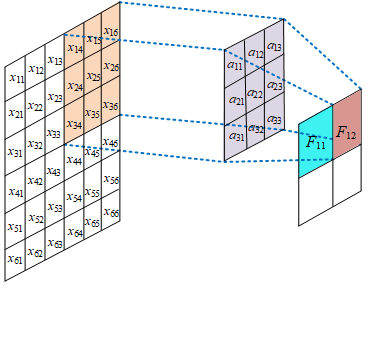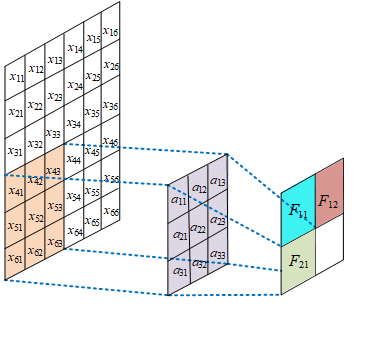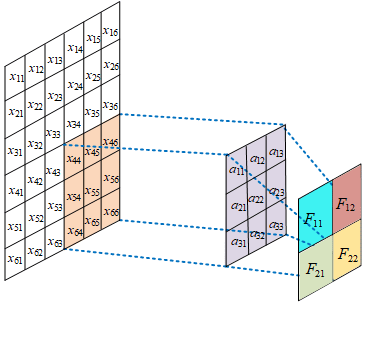
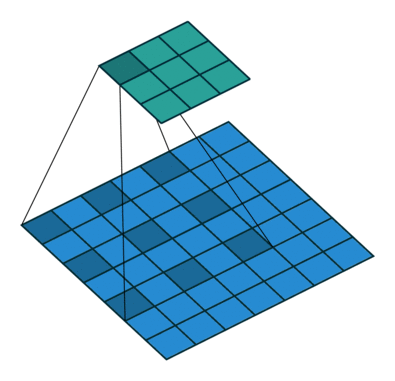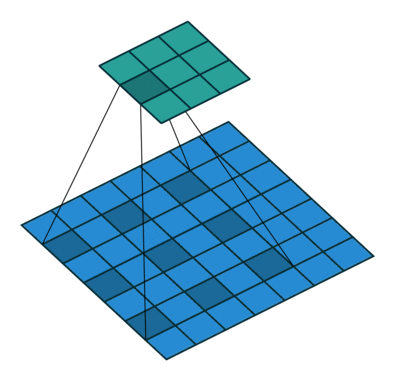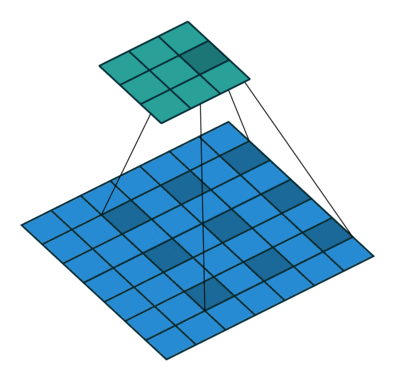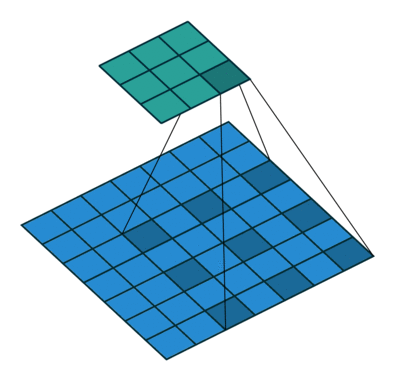
使用卷积过滤器 (convolutional filter) 扫描图像矩阵的过程，对感受野(receptivefield) 内的元素之间作哈达玛积，然后将结果矩阵相加，得到本次的扫描值
在传统图像处理中，人们通过设定不同的算子来提取诸如边缘、水平、垂直等固定的特征。而在卷积神经网络中，仅需要随机初始化一个固定卷积核大小的滤波器，并通过诸如反向传播的技术来实现卷积核参数的自动更新即可。其中，浅层的滤波器对诸如点、线、面等底层特征比较敏感，深层的滤波器则可以用于提取更加抽象的高级语义特征，以完成从低级特征到高级特征的映射

卷积神经网络的特性？

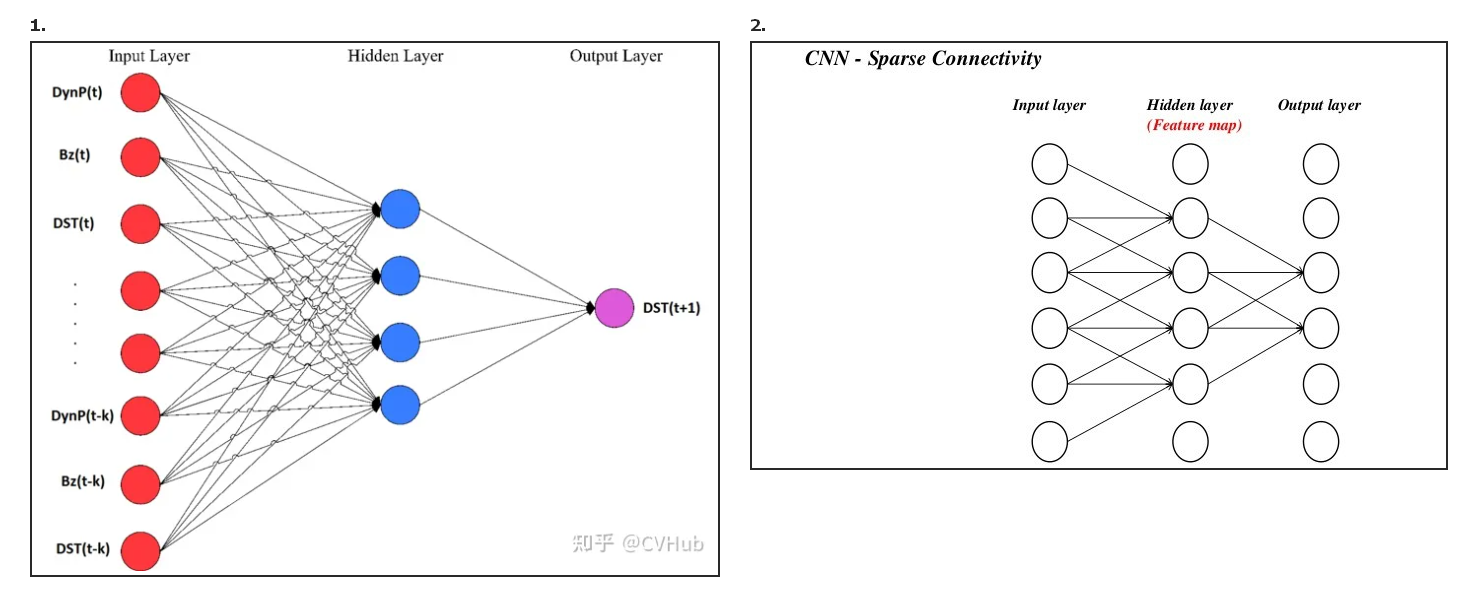
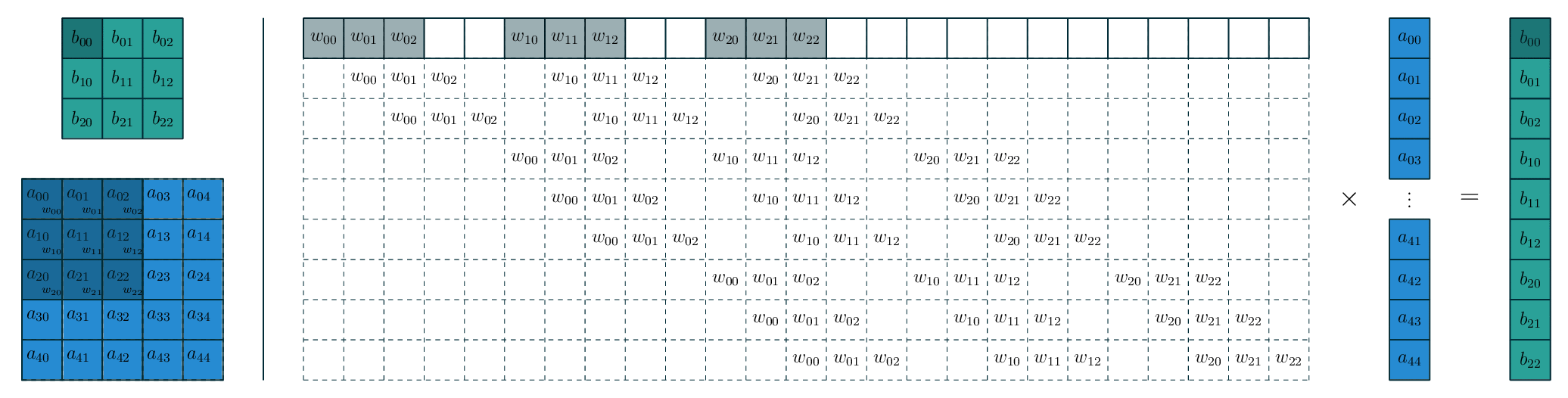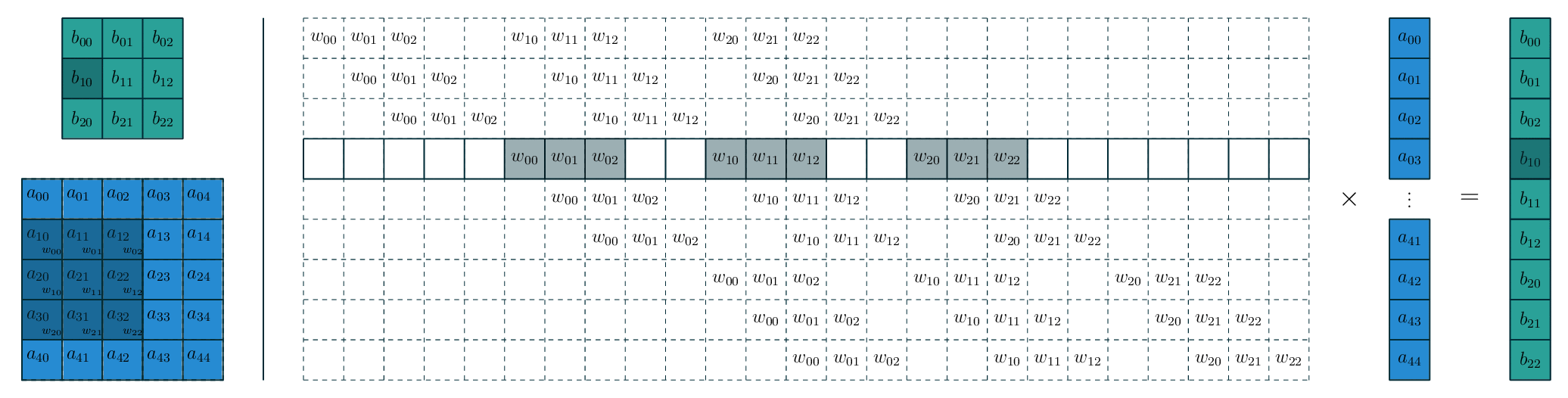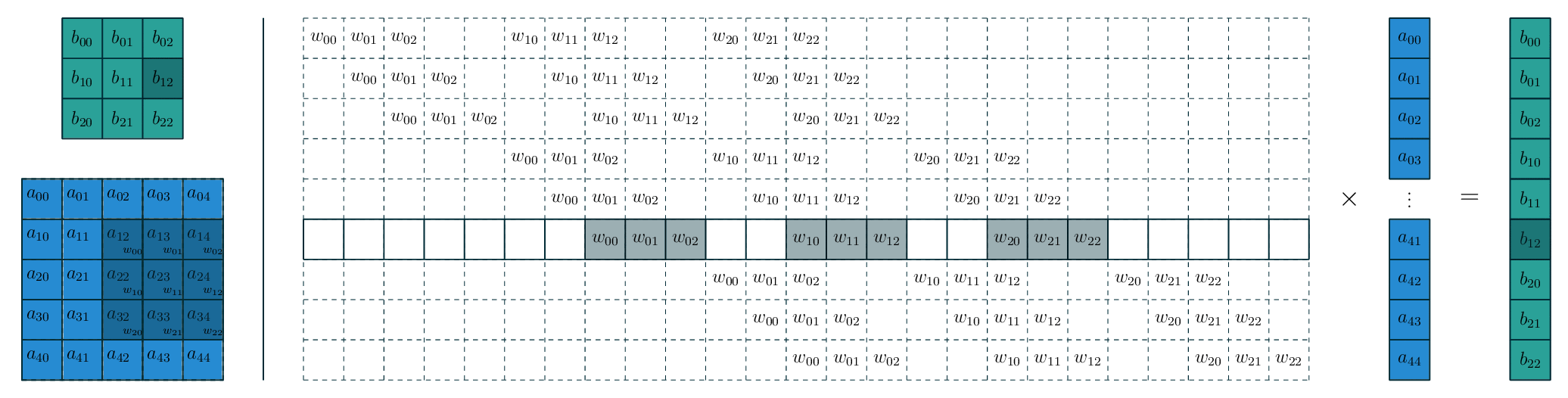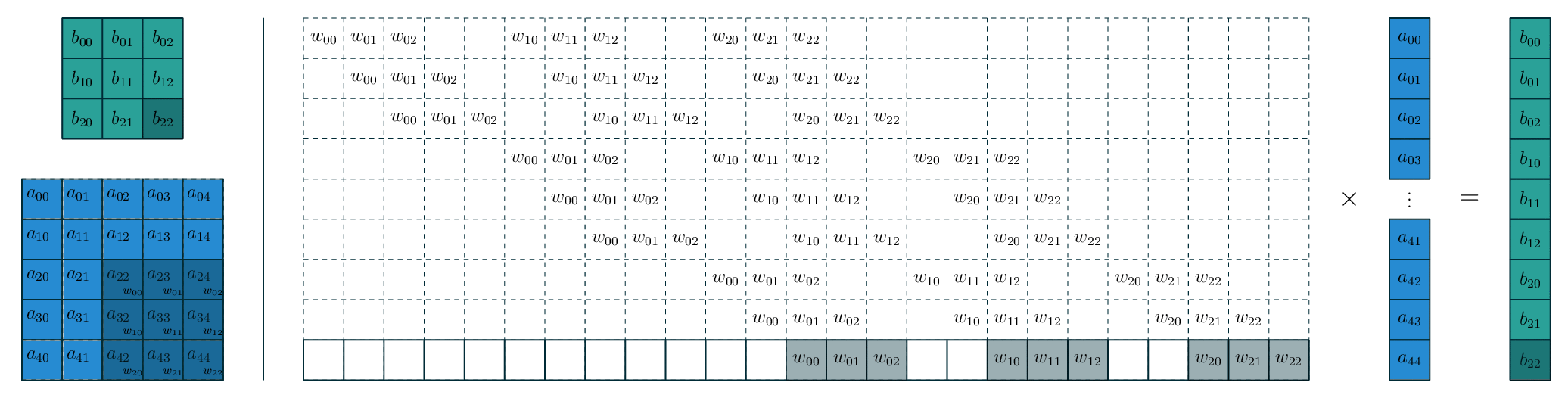
稀疏连接(sparseconnectivity)：传统的神经网络层每个输出单元与每个输入单元进行密集交互；卷积网络只与当前卷积核窗口内的输入交互，因此其连接是稀疏的。在 VGG中，全连接层可以转换为卷积层，但是转换后的卷积核非常多，远大于实际使用的卷积核个数
权重共享(shared weights)：在传统的神经网络中，任意输出单元与任意输入单元都有一个唯一权重描述，而 CNN 只使用卷积核大小的权重描述输入与输出的关系，因此权重被多个输入区域共享
平移不变性(translationalinvariance)：指当图像中的目标发生偏移时网络仍然能够输出同源图像一致的结果。对于图像分类任务来说，我们希望 CNNs 具备平移不变性，因为当图像中目标发生位置偏移时其输出结果应该保持一致
平移等变性 (translation equivalence)：指的是当输入发生偏移时网络的输出结果也应该发生相应的偏移。这种特性比较适用于目标检测和语义分割等任务
大小不变性(sizeinvariance)：指当图像中的目标发生缩放时网络仍然能够输出同源图像一致的结果
旋转不变性(rotationalinvariance)：指当图像中的目标发生旋转时网络仍然能够输出同源图像一致的结果，旋转不变性是相对的，得看实际的目标是否是旋转对称的

如何认识卷积神经网络的稀疏连接 (sparse connectivity)？

相比较全连接层，卷积层的节点仅仅和其前一层的部分节点相连接，只用来学习局部特征

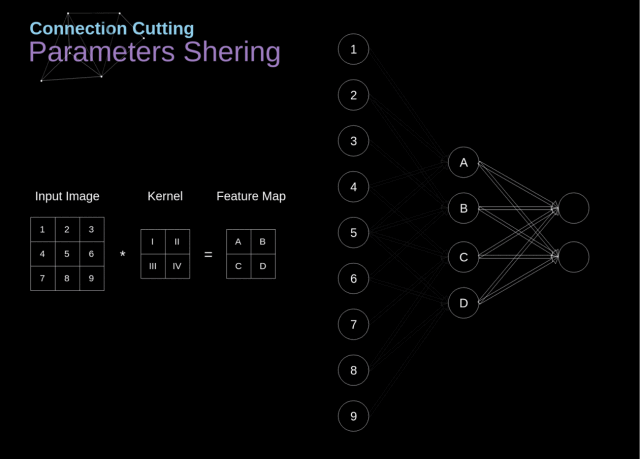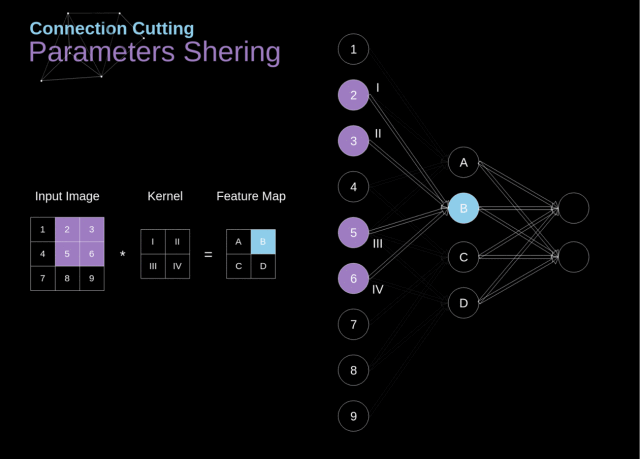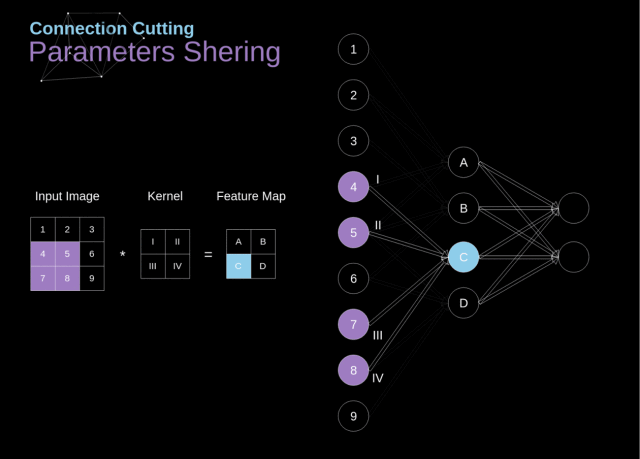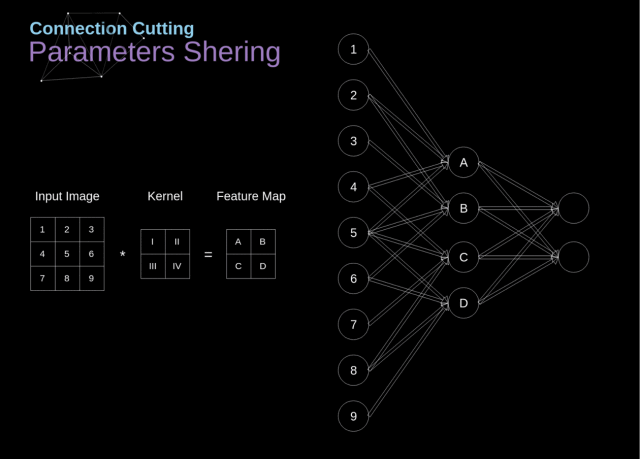
如何认识卷积神经网络的权重共享(shared weights)？

权值共享就是滤波器共享，滤波器的参数是固定的，即是用相同的滤波器去扫一遍图像，提取一次特征特征，得到feature map

什么是卷积过滤器/卷积核(convolutional filter)?

也称卷积核，是一种矩阵，与输入矩阵相比，其形状小很多

对图片数据，为什么不展平使用全连接层去学习，而是使用卷积？

输入数据的空间信息被丢失： 空间上相邻的像素点往往具有相似的RGB值，各个通道之间的数据通常密切相关，但是转化成1维向量时，这些信息被丢失
模型参数过多，容易发生过拟合 (overfitting)：每个像素点都要跟所有输出的神经元相连接。当图片尺寸变大时，输入神经元的个数会按图片尺寸的平方增大，导致模型参数过多，容易发生过拟合

如何从卷积输入计算输出大小？

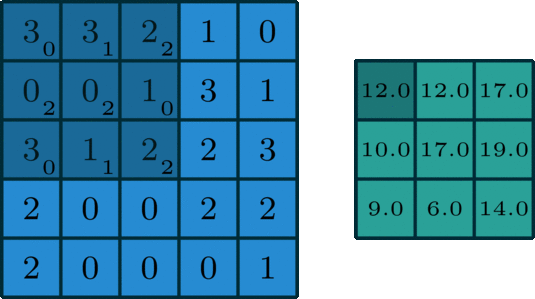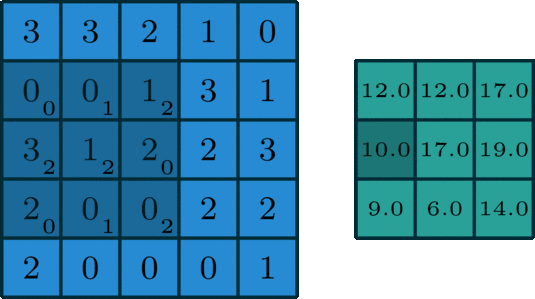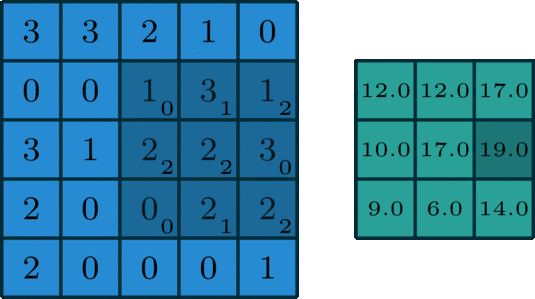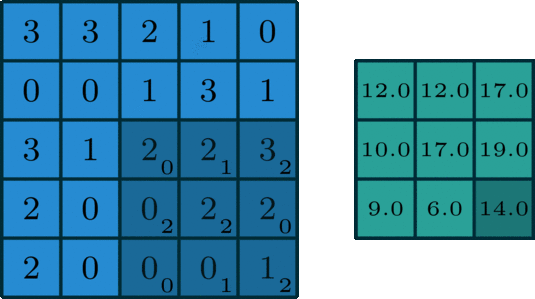
根据输入 i、卷积核大小 k、是否填充 p、步幅长度 s 计算输出大小 $o=\left\lfloor\frac{i+2 p-k}{s}\right\rfloor+1$

单通道输入时，如何计算卷积神经网络输出值？

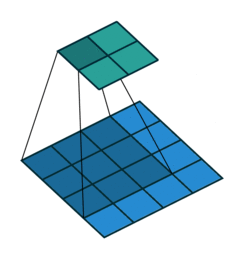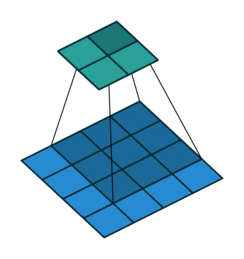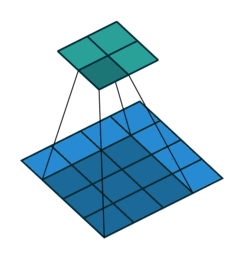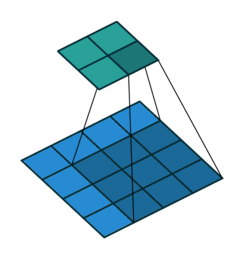
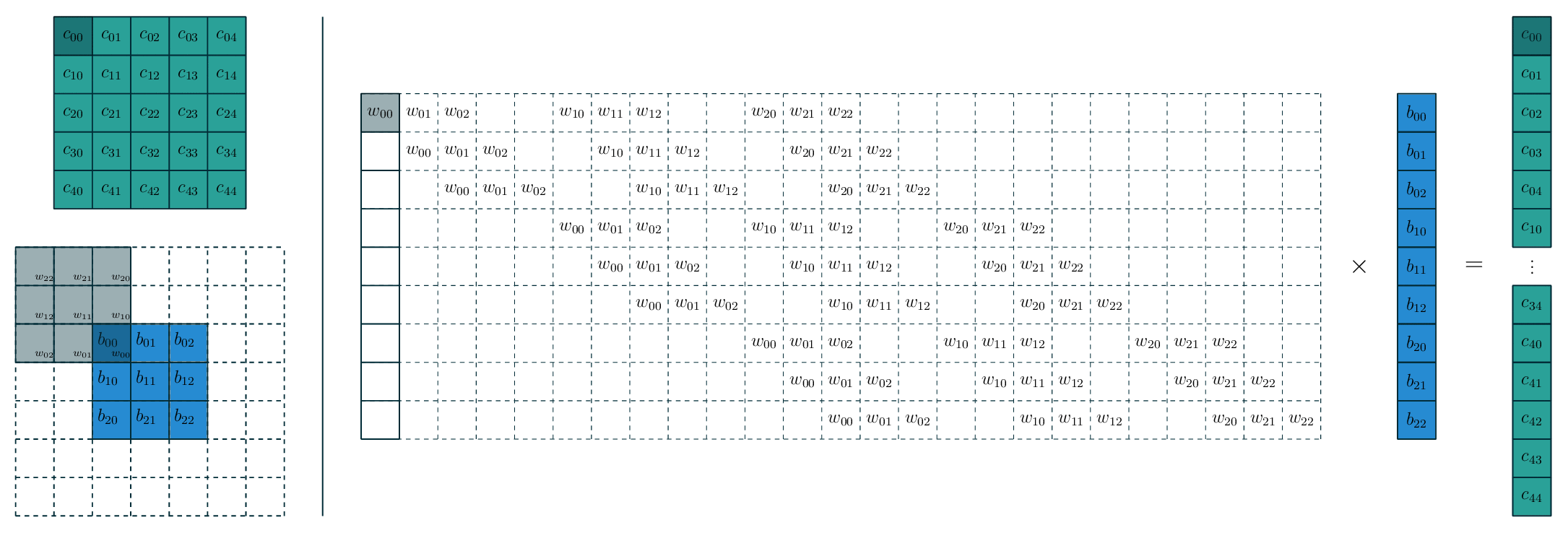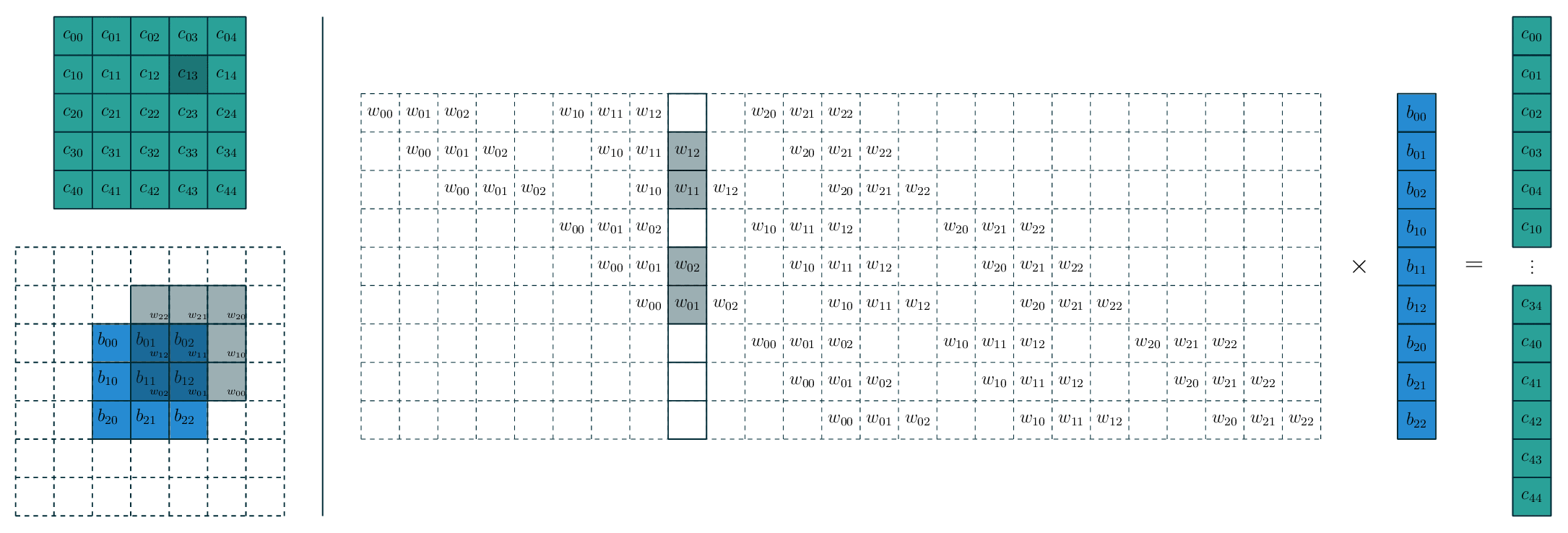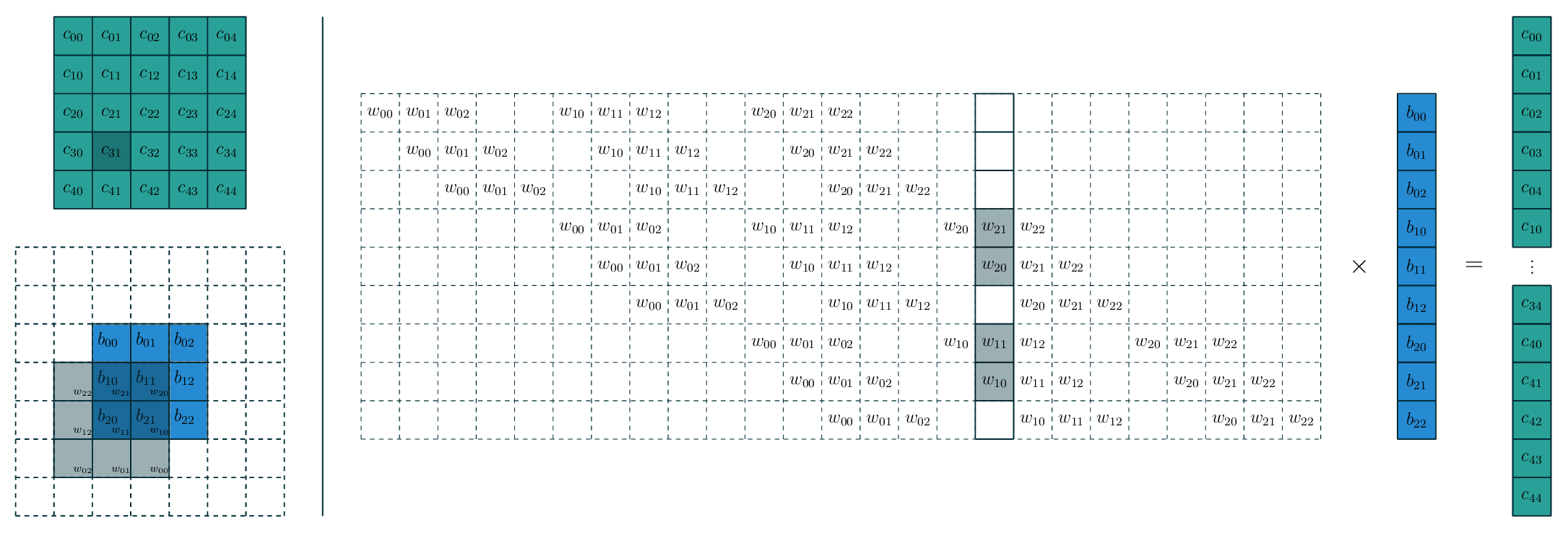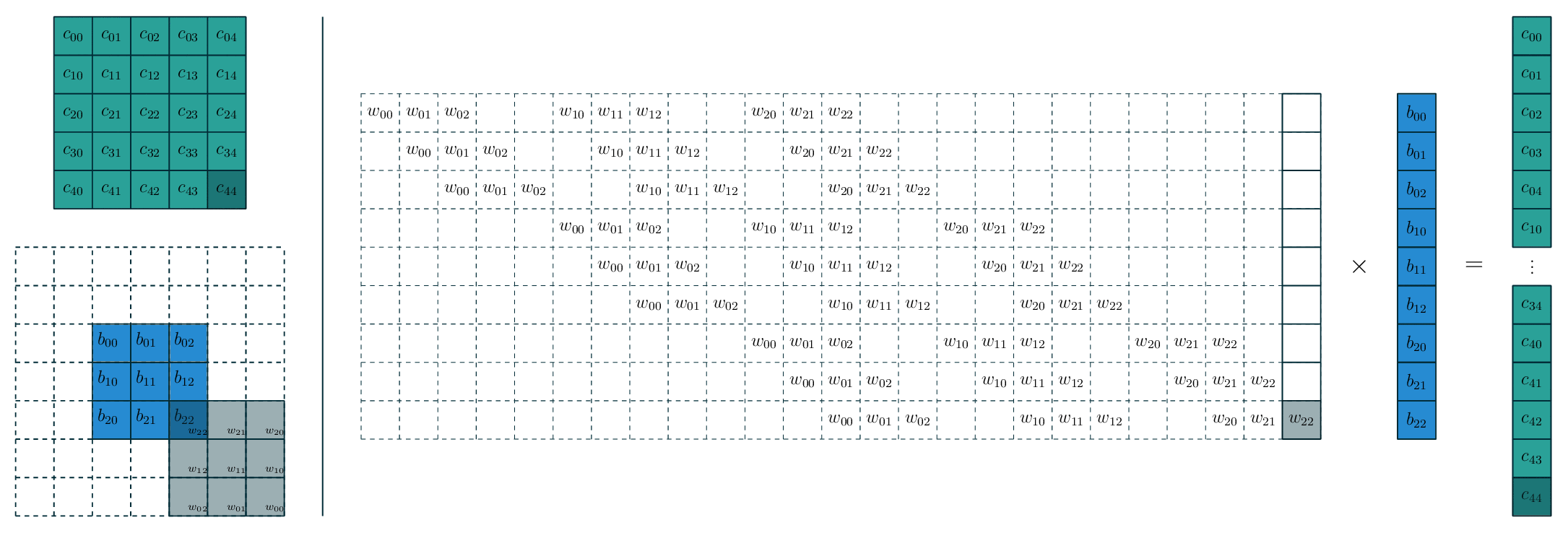
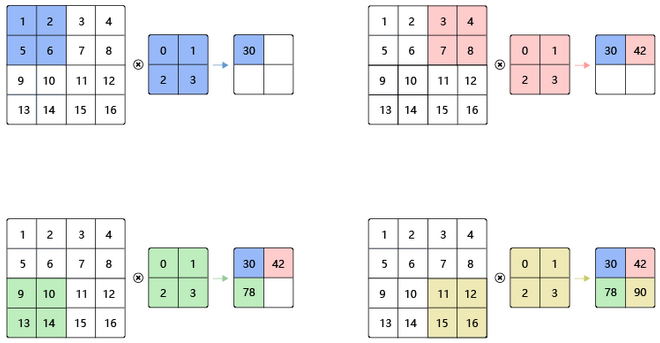
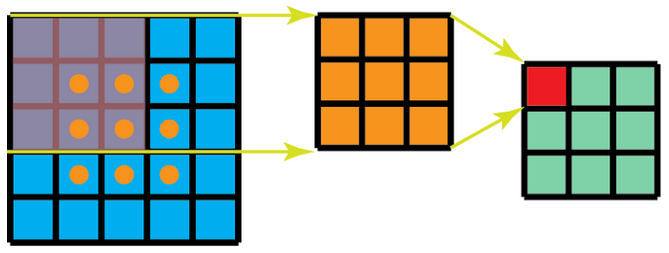
假设有一个 5x5 的图像，使用一个 3x3 的 filter 进行卷积，想得到一个 3x3 的 Feature Map，如图所示

多通道输入时，如何计算卷积神经网络输出值？

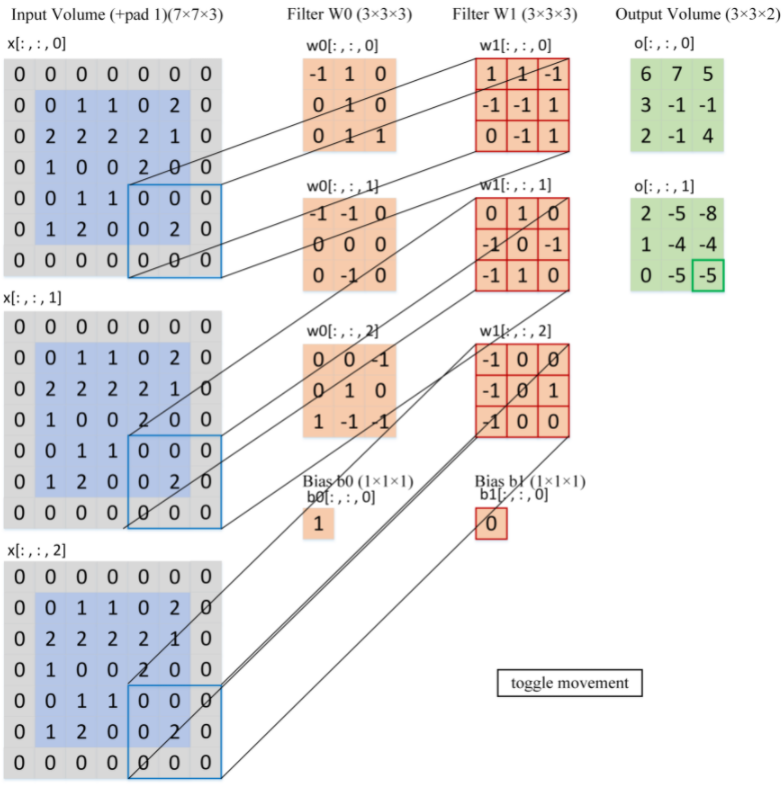
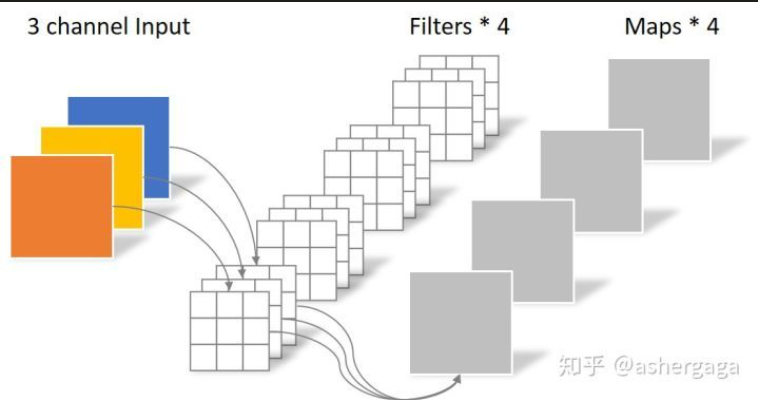
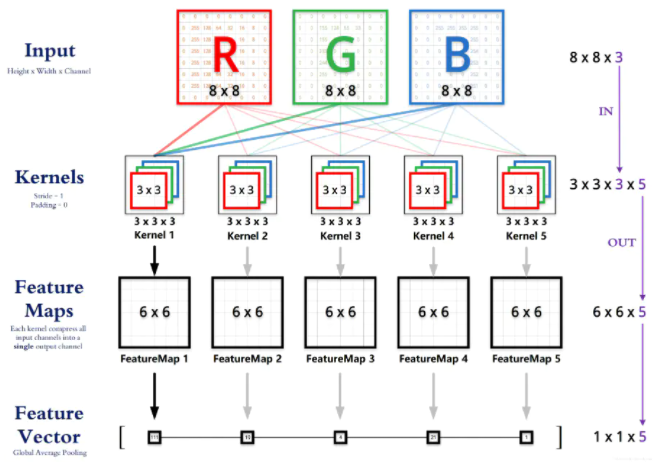
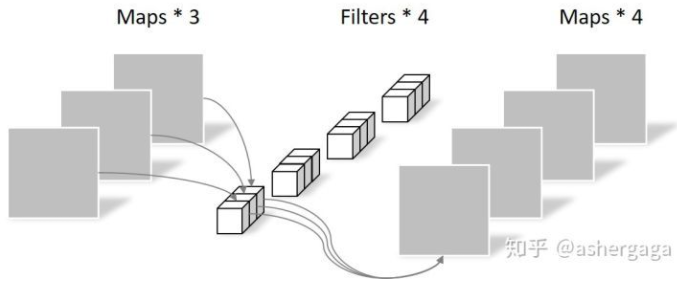
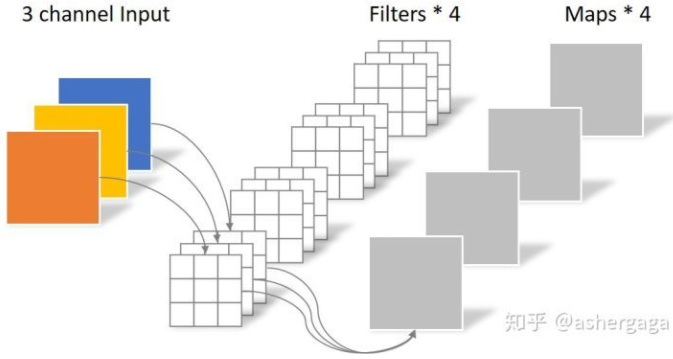
现有 7 x7 x3 输入，假设使用卷积 kernel_size=3x3，pad=1，output_channel=2 对右下角区域 (3 x 3)进行卷积，得到输出为 3x3x2，如果对整个输入进行卷积，将得到 6 x 6 x 2 的输出
根据输出特征的数量 n，使用 n 批卷积核，每批卷积核使用 m 个卷积核去提取特征，上图使用 2 批，每批 3 个卷积核提取特征

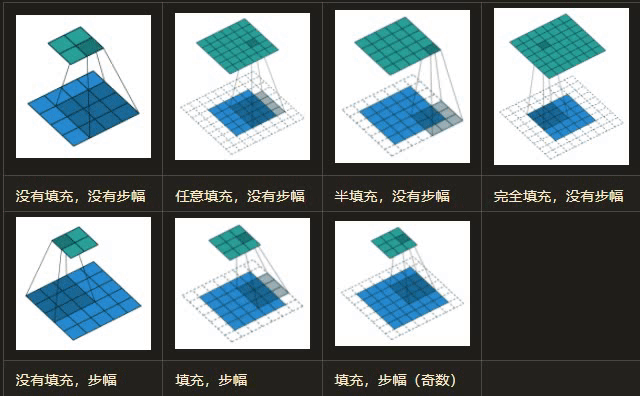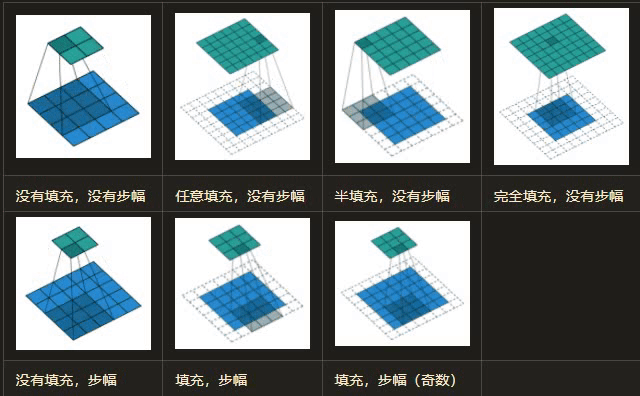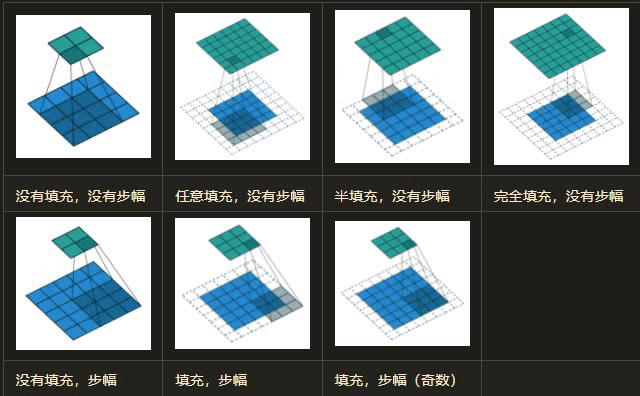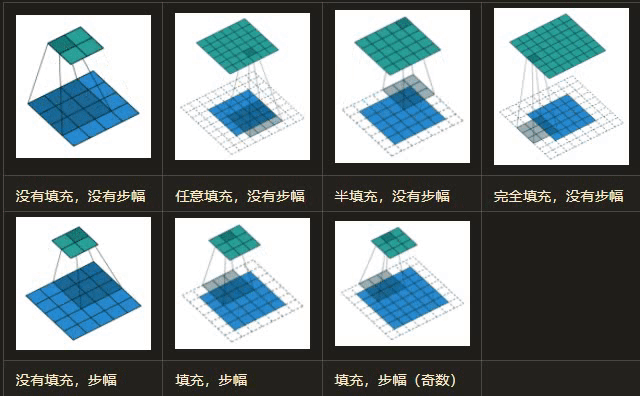
在卷积过程中，如何理解填充(Padding)?

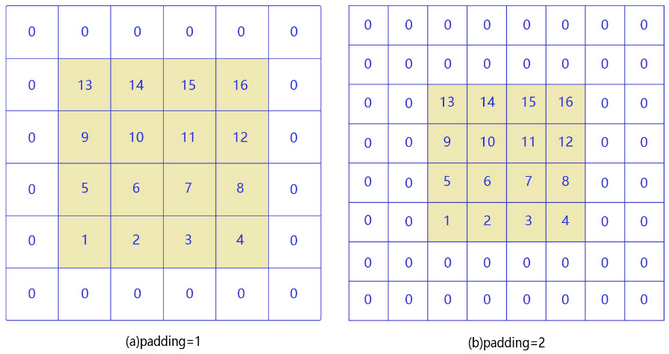
正常卷积过程中，输入图像的边缘像素无法参与卷积计算，为了使边缘像素也参与卷积滤波，填充技术应运而生。填充是指在边缘像素点周围填充“0”（即0填充），使得输入图像的边缘像素也可以参与卷积计算

在卷积过程中，如何理解步长(Stride)?

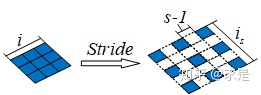
在卷积操作时，通常希望输出图像分辨率与输入图像分辨率相比会逐渐减少，即图像被约减。因此，可以通过改变卷积核在输入图像中移动步长大小来跳过一些像素，进行卷积滤波
当Stride=1时，卷积核滑动跳过1个像素，这是最基本的单步滑动，也是标准的卷积模式。Stride=k表示卷积核移动跳过的步长是k，如图是步长为2的卷积过程

卷积层的参数量及计算量(FLOPs)？

参数量：以2D 卷积为例，卷积核的参数是 $C_{\text {in }} * C_{\text {out }} * K_{h} * K_{w}$ ，每个输出通道有1个 bias，所以卷积的参数量为： $\text { Param }_{\text {conv2d }}=C_{\text {in }} * C_{\text {out }} * K_{h} * K_{w}+C_{\text {out }}$
计算量：以2D 卷积为例，计算输出 featrue map 的每个点时，所有的参数均参与（不考虑 bias，需要减1），所以卷积的 FLOPs 如下，其中 $HWC_{out}$ 表示输出特征图有多少个元素， $2\times C_{in}K^2-1$ 表示原特征图需要计算多少次得到输出特征图上的一个点，需要 $C_{in}K^2$ 个乘法和 $C_{in}K^2$ 个加法： $FLOPs =B\times\underbrace{HWC_{out}}\times\overbrace{(2\cdot C_{in}K^2-1)}$

卷积核一般为奇数？

保证锚点刚好在中间，方便以 central pixel为标准进行滑动卷积，避免了位置信息发生偏移
保证在填充（Padding）时，在图像之间添加额外的零层，图像的两边仍然对称

卷积核是不是越大越好？

AlexNet中用到了一些非常大的卷积核，比如11×11、5×5卷积核，之前人们的观念是，卷积核越大，感受野越大，看到的图片信息越多，因此获得的特征越好。但是大的卷积核会导致计算量的暴增，不利于模型深度的增加，计算性能也会降低
在 VGG、Inception 网络中，利用2个3×3卷积核的组合比1个5×5卷积核的效果更佳，同时参数量（3×3×2+1=19<26=5×5×1+1）被降低，因此后来3×3卷积核被广泛应用在各种模型中
总结：增加核函数的大小不一定会提高性能。这个问题在很大程度上取决于数据集

不同卷积核作用图像的效果?

什么是卷积神经网络的宽度？

所谓宽度，卷积神经网络中的通道数，通道数越多越宽

什么是特征图(featrue map)？

任意大小、任意维度信息矩阵的统称，指在卷积神经网络中卷积滤波结果矩阵

什么是感受野(receptive field)？

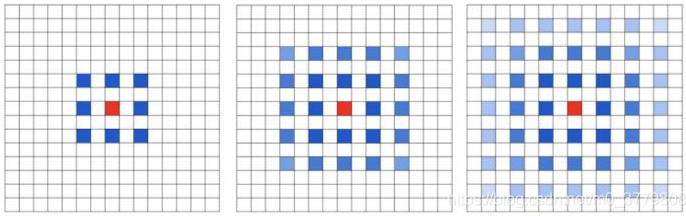
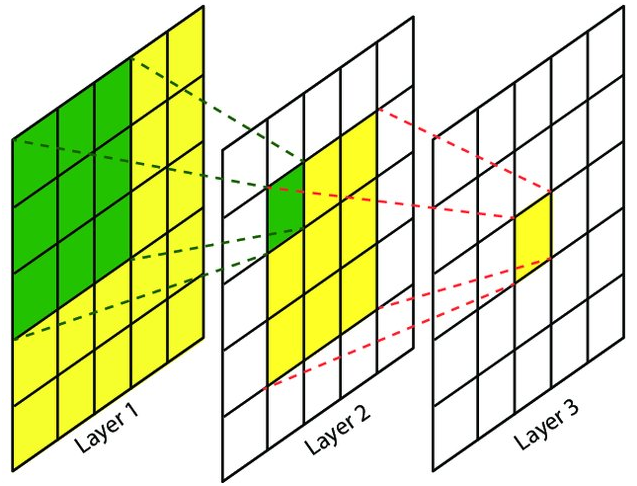
指的是卷积神经网络每一层输出的特征图(featrue map)上的像素点在原始图像上映射的区域大小
上图是2个3x3卷积(stride=1)，layer2上绿色点的layer1感受野为绿色区域， layer3上黄色点的layer2感受野为黄色区域，同时在layer1上感受野是黄色区域
第一层卷积层的输出特征图像素的感受野的大小等于滤波器的大小；深层卷积层的感受野大小和它之前所有层的滤波器大小和步长有关系

增大感受野的方式？

加深网络，如 VGGNet
使用空洞卷积(Atrous convolution)

什么是1x1卷积？

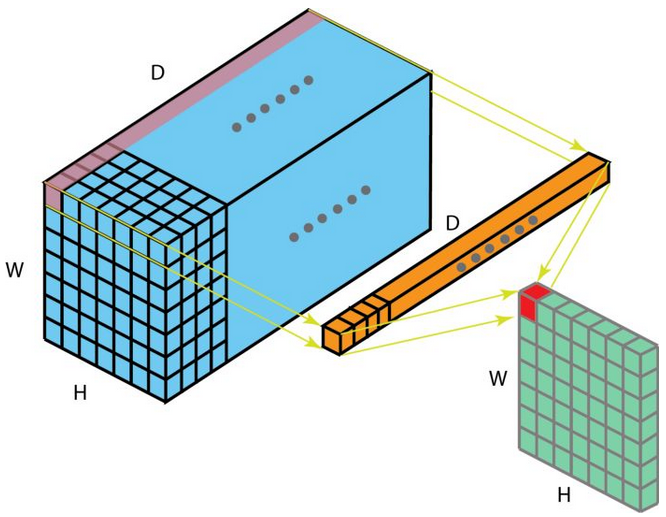
在一个维度为 H x W x D 的输入层上的操作方式。经过大小为 1 x 1 x D 的filters的 1 x 1 卷积，输出通道的维度为 H x W x 1
NIN是第一篇探索1x1卷积核的论文，这篇论文通过在卷积层中使用MLP替代传统线性的卷积核，使单层卷积层内具有非线性映射的能力
GoogleNetv1 使用1x1卷积核减少模型参数量。在原始版本的Inception block中，由于每一层网络采用了更多的卷积核，大大增加了模型的参数量。此时在每一个较大卷积核的卷积层前引入1x1卷积，可以通过分离通道与宽高卷积来减少模型参数量

1 x 1 卷积的作用？

增强特征表达能力：1×1卷积本质上也是一个带参数的滤波器，在不改变特征图本身尺寸的情况下，能够增加网络深度。通过在卷积后通过非线性激活函数可以有效的增强网络的表达能力
升维和降维：1×1卷积可以通过增加或减少滤波器的数量来实现升维或降维的目的。与全连接层不同，由于卷积是基于权值共享，因此能够有效的降低网络的参数量和计算量
跨通道的信息交互：类似于多层感知机，1×1卷积本质上就是多个特征图之间的线性组合。因此，通过1×1卷积操作可以轻松实现跨通道的信息交互和整合

什么是反卷积(deconvolution)?

反卷积也被称为转置卷积，反卷积其实就是标准卷积(Convolution)的逆过程，是一种上采样技术
反卷积操作并不能还原出卷积之前的图片，只能还原出卷积之前图片的尺寸

如何进行反卷积 (deconvolution)?

通过对原始特征矩阵进行填充使其维度扩大，然后进行普通卷积的过程

反卷积的输入输出大小计算？

假设输入矩阵大小为 i，填充为 p，步幅为 s，卷积核为 i
第一步：对输入进行 stride 变换，stride 可理解为为在输入的相邻元素之间添加 s−1 个零元素。变换后的尺寸为 $i_s=i+(s-1)(i-1)$
第二步：对 stride 变换后的图片按照卷积形式求解输出尺寸 $o=s(i-1)+2p-k+2$

卷积与反卷积的关系？

卷积：stride=1
反卷积：padding=1， stride=1
反卷积的本质还是卷积，他们并不是互为逆运算的，仅仅是在形状上存在互逆的关系

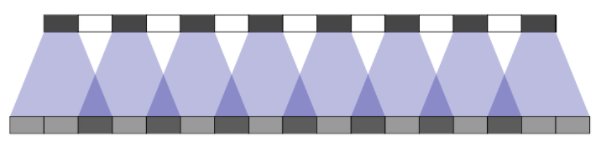
什么是反卷积(deconvolution)的棋盘效应？

在使用转置卷积时观察到一个棘手的现象（尤其是深色部分常出现）就是"棋盘格子状伪影"，被命名为棋盘效应（Checkboard artifacts）

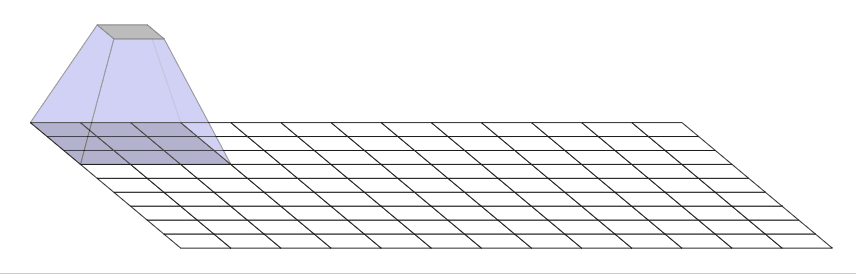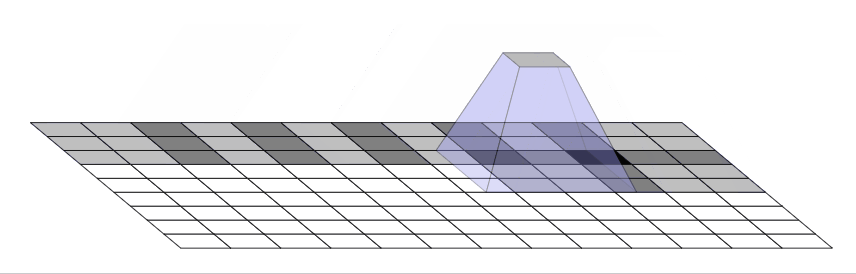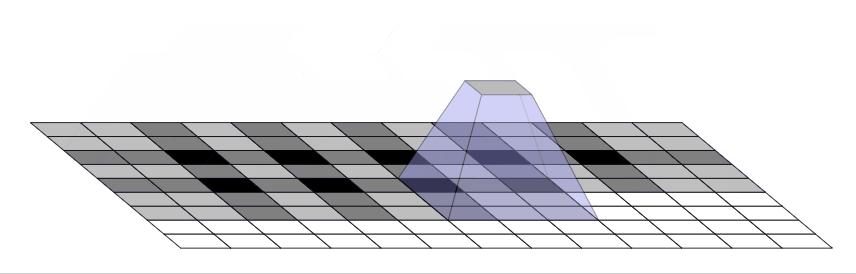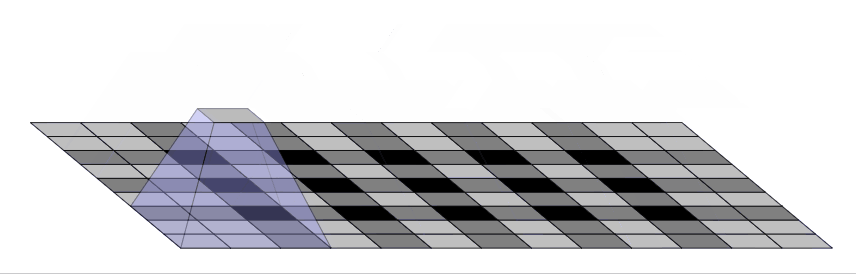
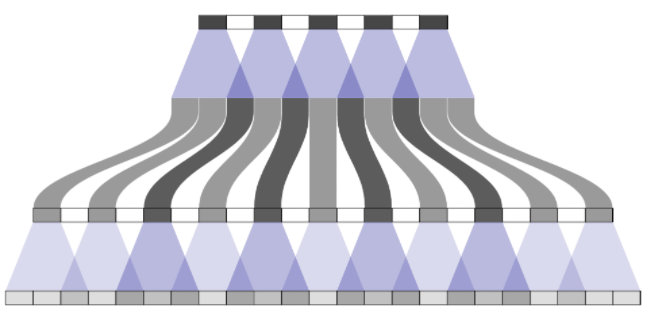
为什么反卷积会出现棋盘效应？

当内核大小（输出窗口大小）不能被步幅整除时，反卷积具有不均匀的重叠
重叠图案也以二维形式形成。两个轴上的不均匀重叠相乘在一起，形成了不同大小的典型棋盘状图案
神经网络在创建图像时通常使用多层反卷积，从一系列较低分辨率的描述中迭代构建更大的图像。虽然这些堆叠的反卷积可以消除伪影，但它们通常会复合，在各种尺度上产生伪影

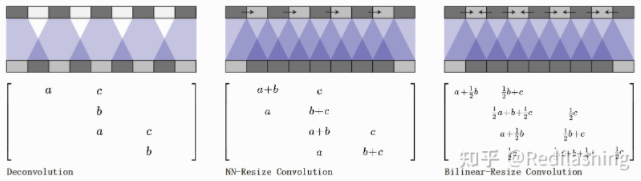
如何抑制反卷积(转置卷积)的棋盘效应？

方法一：确保使用整除步幅的内核大小，避免重叠问题。 这相当于“亚像素卷积”。然而虽然这种方法有帮助，但反卷积仍然很容易陷入创建伪影
方法二：将上采样到更高分辨率从卷积中分离出来以计算特征。 例如，可以调整图像大小（使用最近邻插值或双线性插值），然后进行卷积层

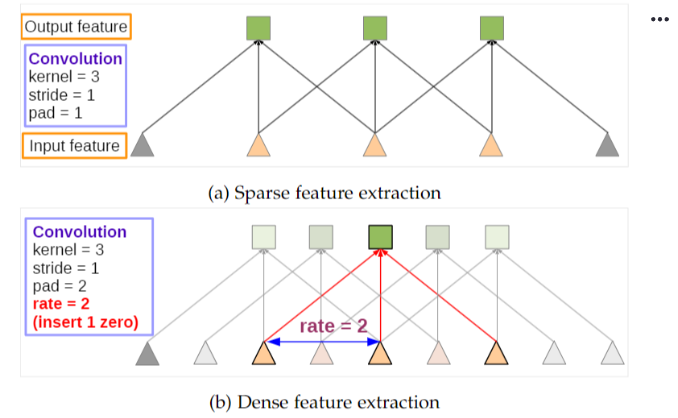
什么是空洞卷积(Atrous convolution)？

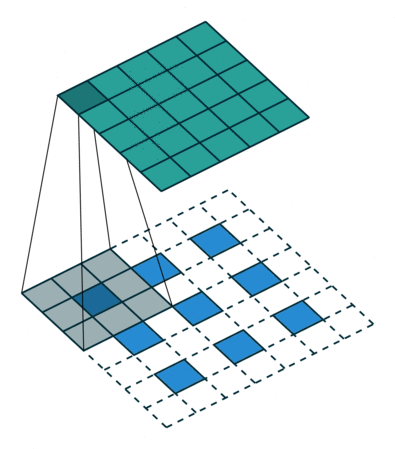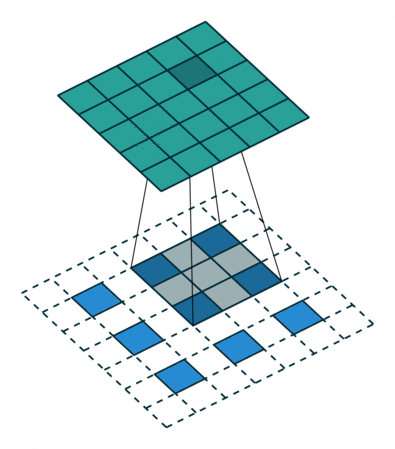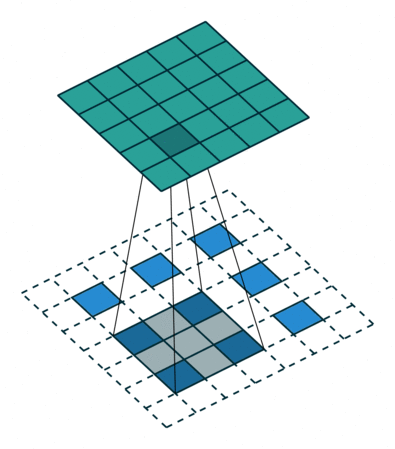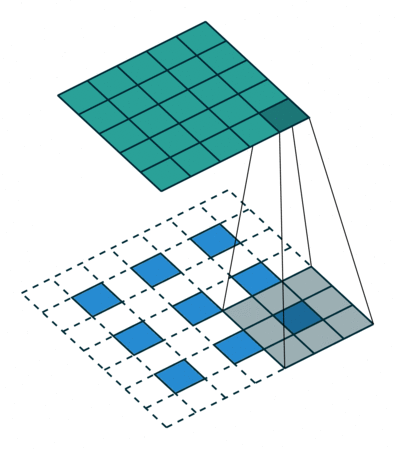
也称为扩张卷积 (Dilated Convolution)，是DeepLabv1在标准卷积的基础上引入扩张率 r (Dilation) 参数，在卷积核之间插入 r-1 个 0，将 $k*k$ 的卷积核扩展为 $k+(k-1)*(r-1)$ ，此时卷积核的感受野出现空洞
相同尺寸的空洞卷积拥有更大的感受视野，相同视野情况下比普通卷积更少的参数，如图同样是 $3\times3$ 的卷积核尺寸，空洞卷积可以提取 $5\times5$ 范围的区域特征

根据卷积的输出计算公式 torch. Nn. Conv 2 d，卷积核为 3 x 3 的空洞卷积，只要其 padding=dilation，卷积层输出的大小保持不变。空洞卷积金字塔池化 (Atrous Spatial Pyramid Pooling，ASPP) 正是利用这一点进行多路的空洞卷积

>>> input = torch.randn(5, 8, 56, 128)
>>> m = torch.nn.Conv2d(8, 33, (3, 3), padding=(4, 4), dilation=(4, 4));m(input).shape
torch.Size([5, 33, 56, 128])
>>> m = torch.nn.Conv2d(8, 33, (3, 3), padding=(24, 24), dilation=(24, 24));m(input).shape
torch.Size([5, 33, 56, 128])

空洞卷积的作用？

增大感受野：空洞卷积可以在同等卷积核参数下获得更大的感受野。对于需要较为全局的语义信息或类似于语音文本需要较长的序列信息依赖的任务中，都可以尝试应用空洞卷积
表征多尺度信息：利用带有不同空洞率的卷积，还可以捕捉到多尺度的上下文语义信息。不同的空洞率代表着不同的感受野，意味着网络能够感知到不同尺寸的目标，例如 DeepLabv3 、DeepLabv3+

空洞卷积的2种实现方式？

从kernel角度：相当于在标准kernel的相邻点之间添加r-1个0
从原图角度：使用标准kernel，在原图每隔r-1行进行卷积采样(DeepLabv2用的这一种)

空洞卷积有什么缺点？

不好优化：虽然引入空洞卷积可以在参数不变的情况增大感受野，但是由于空间分辨率的增大，所以在实际中常常会不好优化，速度方面是一个诟病，因此在工业上对实时性有要求的应用更多的还是类FCN结构
网格效应：多次叠加r=2 的 3 x 3kernel，发现 kernel 并不连续，也就是并不是所有的 pixel 都用来计算了，因此这里将信息看做 checker-board 的方式会损失信息的连续性。这对 pixel-level dense prediction 的任务来说是致命的
长空洞对小物体不友好： 采用大 dilation rate 的信息或许只对一些大物体分割有效果，而对小物体来说可能则有弊无利了，HDC 可以解决该问题

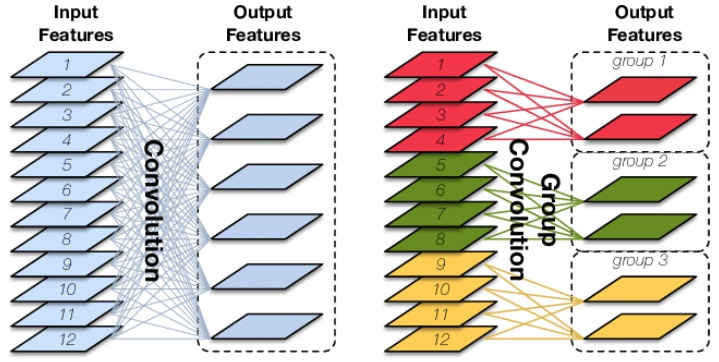
什么是分组卷积(Group Convolution) ?

AlexNet为了使得大卷积层能在小GPU上训练，将卷积层的filter分组到2个GPU上训练，这是最早的分组卷积，ResNeXt 则将分组卷积系统地提出，并说明分组卷积类似给模型加上正则化一样，使得模型学习更准确
现有输入特征 CxHxW，N 个 KxK 卷积核，以下是标准卷积和分组卷积（G 组）的参数量比较，可以发现分组卷积的参数量是标准卷积的 $\frac 1 G$ $\begin{array}{}{C_0}\times K \times K \times C_1 \\ \frac{C_0}{G}\times K\times K\times \frac{C_1}{G} \times G \end{array}$

分组卷积的作用？

减少参数量：分为 G 组后，分组卷积 (Group Convolution) 的参数量减少为标准卷积 (Convolution) 的 $\frac{1}{G}$
提高训练效率：通过将卷积运算按通道划分为多个路径，可以尽可能地利用分布式的计算资源进行并行运算，有利于大规模深度神经网络的训练
提高泛化性能：组卷积可以看成是对原始卷积操作的一种解耦，改善原始卷积操作中滤波器之间的稀疏性，在一定程度上起到正则化的作用，即由标准卷积的 $C*K*K$ 卷积核变为 $\frac{C} {G}*K*K$ ，相当于其他 $(C-\frac{C}{G}) *K*K*N$ 个卷积核的参数为 0

为什么分组卷积有用？

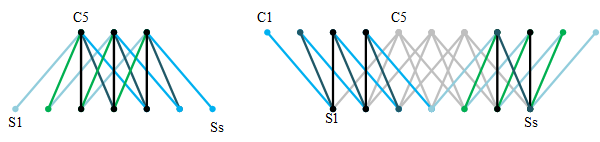
其实就是对卷积过滤器进行稀疏。如图是在CIFAR10上训练的NIN模型中，相邻层filters之间的相关矩阵（越亮相关性越高），当使用1、2、4、8和16个filters组训练时，在CIFAR10上训练的NIN模型中相邻层filters之间的相关性
分组后的filters同组的filter的相似性更高，类似给filters加上强制化的“结构”约束信息，即对模型进行了正则化处理，使得模型学习更准确
正如通过分组在不同GPU训练的AlexNet那样，它的filters组似乎将学习到的filters分为两个不同的组，即黑白filter和彩色filter，第一组学习纹理信息，第二组学习颜色信息，其学习的重点不同分组不同

分组卷积与深度可分离卷积的关系？

在分组卷积(Group Convolution) 中，如果输入特征图数量、输出特征图数量、分组数量都相等，即C=N=G，此时，卷积核大小为 $\frac{C} {G}*K*K=1*K*K$ ，这和深度可分离卷积(depthwise separable convolution) 的通道卷积一致
由此可知，分组卷机是标准卷积(Convolution)和深度可分离卷积的一个折中方案

分组卷积与全局深度卷积(GDC)的关系？

在分组卷积中，如果输入特征图数量、输出特征图数量、分组数量都相等，即 C=N=G，在进一步，如果卷积核尺寸等于输入特征图尺寸，即 K=H=W，那么输出是 Cx1x1长度为 C 的向量，此时称为 Global Depthwise Convolution (GDC)
与全局池化(Global Pooling) 不同的是，GDC 给每个位置赋予了可学习的权重（对于已对齐的图像这很有效，比如人脸，中心位置和边界位置的权重自然应该不同），而GAP每个位置的权重相同，全局取个平均

分组卷积的局限性？

分组卷积将输入层的不同特征图进行分组，然后采用不同的卷积核再对各个组进行卷积，这样会降低卷积的计算量。因为一般的卷积都是在所有的输入特征图上做卷积，可以说是全通道卷积，这是一种通道密集连接方式，而分组卷积相比则是一种通道稀疏连接方式
1)计算量矛盾： 分组卷积在输入特征图数量、输出特征图数量、分组数量都相等的情况下，退变为深度可分离卷积(depthwise separable convolution) ，此时存在大量的1x1卷积
2)特征通信矛盾： 分组后的卷积不同组之间的不会进行通信，会降低网络的特征提取能力，所以 Xception，MobileNet 通过密集的1x1卷积，保证不同组的特征的交流，为了让不同组的特征进行交流，除了使用1x1卷积，ShuffleNetv1 还提出将不同组的特征混淆来实现特征重组

什么是深度可分离卷积?

深度可分离卷积(depthwise separable convolution)分为depthwise(深度计算，逐通道卷积)和pointwise(点计算，逐点卷积)组成，用来提取特征feature map，与标准卷积相比，其参数数量和运算成本比较低
标准卷积：输入5x5x3图像，经过3x3卷积（输出通道为4）
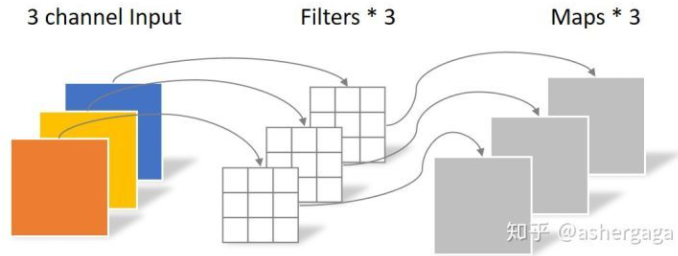
深度可分离卷积：depthwise (深度计算，逐通道卷积) 输入图像，经过3x3深度可分离卷积（输出通道一定为3，因为卷积核的数量与上一层的通道数相同 ）
深度可分离卷积：pointwise (点计算，逐点卷积) ，输入图像，经过 Mx1x1xN 的点卷积，M 为上一层通道，N 为输出通道
depthwise(深度计算，逐通道卷积) 只在某个固定特征图上扫描，提取的是空间特征，pointwise(点计算，逐点卷积) 使用1x1卷积，此时与周围特征无关，只整合通道间的特征
可分离卷积(Seperable Convolution)通常应用在模型压缩或一些轻量的卷积神经网络中，如MobileNet、Xception等

深度可分离卷积的作用？

降低参数量和计算量：深度可分离卷积将原始的卷积运算分为两层，一层用于滤波（深度卷积），一层用于组合（逐点卷积）。这种分解过程能极大减少模型的参数量和计算量
降低模型容量：深度可分离卷积在应用时并没有使用激活函数。此外，虽然深度可分离卷积可以显著的降低模型的计算量，但同时也会导致模型的容量显著降低，从而导致模型精度的下降

深度分离卷积与标准卷积参数量、计算量(FLOPs)的区别？

标准卷积的计算原理
深度可分离卷积(depthwise separable convolution) 将空间卷积和时间卷积(通道卷积)分离，先进行时间卷积(通道卷积)，再进行空间卷积
参数量比较：所谓参数量，指的是卷积核的大小，标准卷积和深度可分离卷积的参数量计算如下，较少的参数意味较少的乘法，也就意味着卷积实现过程通用矩阵乘法(General Matrix Multiply Functions,GEMM)实现执行更快$$\left{\begin{array}{l} D_{kernel} \times D_{kernel}\times M \times N\ D_{kernel} \times D_{kernel}\times M + 1\times 1 \times M \times N \end{array}\right.$$
计算量比较： 参数量乘上特征图尺寸为计算量大小，标准卷积和深度可分离卷积的计算量 $\left\{\begin{array}{l} D_{kernel} \times D_{kernel}\times M \times N\times D_{featrue}\times D_{featrue}\\ D_{kernel} \times D_{kernel}\times M \times D_{featrue}\times D_{featrue} + M \times N \times D_{featrue} \times D_{featrue} \end{array}\right.$
对于卷积核为3的卷积，参数量或计算量为标准卷积的1/9

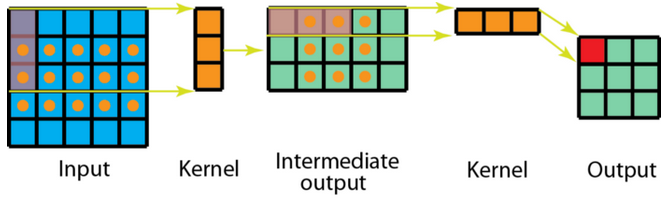
什么是空间可分离卷积？

又称分解卷积(Spatial Separable Convolutions)，在空间维度将标准卷积运算进行拆分，将标准卷积核拆分成多个小卷积核，如3x3的卷积，可分解为3x1的卷积，接上1x3卷积，在执行相同操作时，空间可分离卷积只需要6个参数而不是9个参数
单通道标准卷积
单通道的空间分离卷积
尽管空间可分离卷积节省了成本，但很少在深度学习中使用它。主要原因之一是并非所有kennels都可以分为两个较小的kennels。如果用空间可分离卷积代替所有传统的卷积，在训练过程中，我们将限制卷积核的类型，训练结果可能不是最佳的

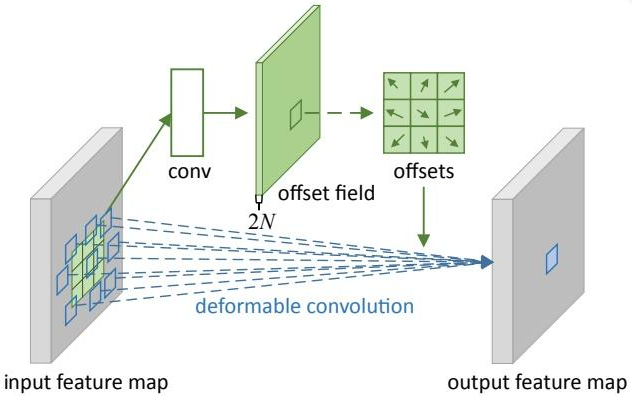
什么是可变形卷积 (Deformable Convolution)?

固定视野的窗口无法适应目标尺寸：传统 CNN 模块，卷积单元在固定位置对输入特征图进行采样，即同一 CNN 层中所有激活单元的感受野大小是相同的，这对于具有精细定位的视觉识别（语义分割）是有害的，因为不同的位置可能对应于具有不同尺度或变形的对象
可变形卷积就是卷积的位置是可变形的，在传统的N×N卷积基础上，通过在每一个卷积采样点加上了一个偏移量实现

可变形卷积的作用？

自适应感受野：传统的卷积核由于尺寸形状固定，其激活单元的感受野也相对固定。但实际上同一个物体由于在不同位置上可能对应着不同的尺度或者变形，因此自适应感受野是进行精确定位所需要的，特别是对于密集型预测任务来说。可变形卷积基于一个平行的网络来学习偏移，让卷积核在输入特征图能够发散采样，使网络能够聚焦目标中心，从而提高对物体形变的建模能力
难以部署：DCN虽然可以带来高精度，但是仍然存在一个缺陷，即当卷积核过大时，会占用非常大的内存空间，因此在落地部署方面的应用很受限制。不过对于参加竞赛而言倒不失为一种提分的trick

什么是延迟卷积（LazyConv2d）

延迟卷积应用于那些输入通道 (in_channel)未知的卷积，实际执行时才知道，才去对卷积参数初始化。所以定义该层不需要像 torch. nn. Conv2d 提供 in_channel 参数
LazyConv2d能够更高效地利用计算资源，因为它只会在需要时才计算

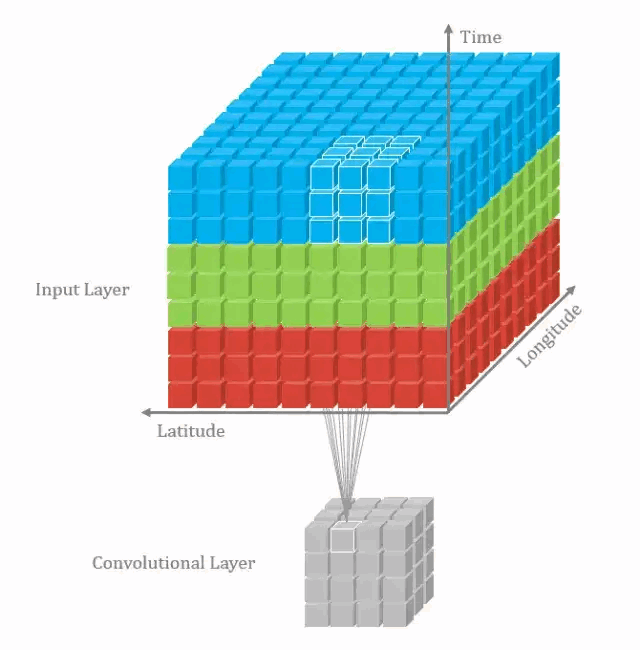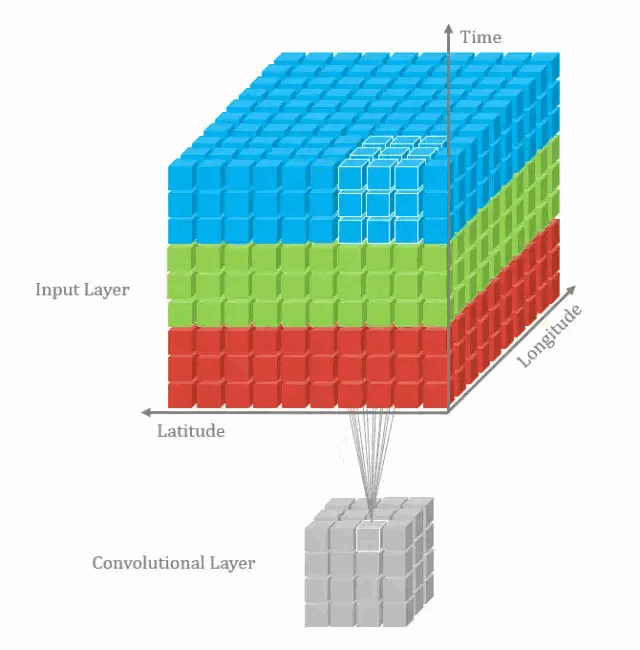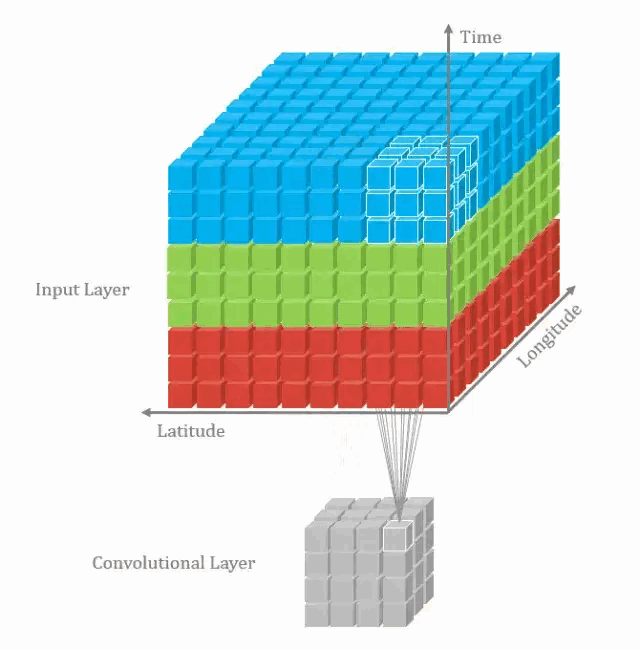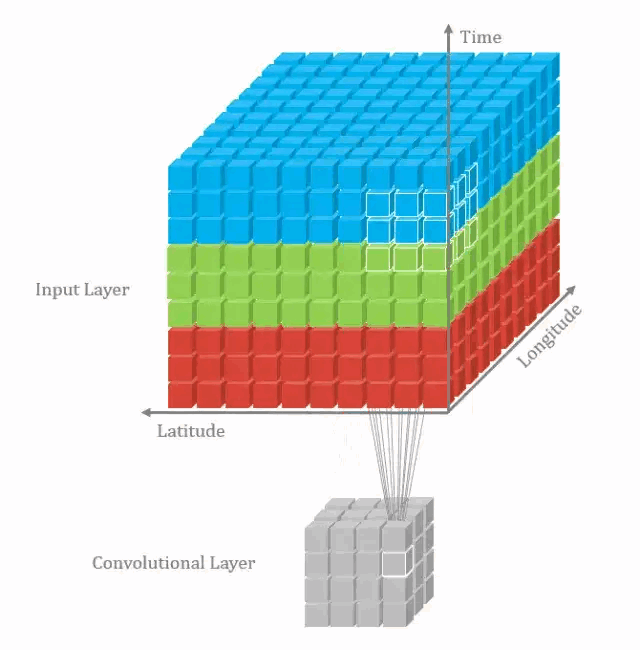
什么是3D 卷积？

2D-卷积和3D-卷积的主要区别为filters滑动的空间维度，3D-卷积的优势在于描述3D空间中的对象关系。3D关系在某一些应用中十分重要，如3D-对象的分割以及医学图像的重构等

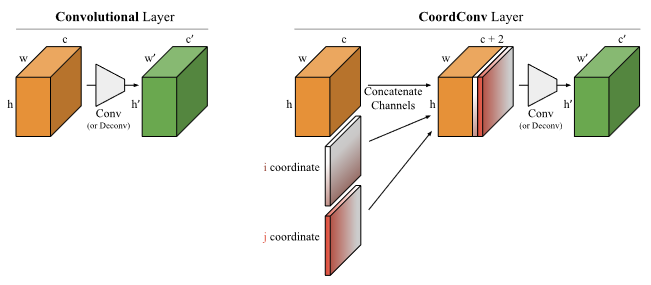
什么是座标卷积 (CoordConv)?

传统卷积具备平移不变性，这使得其在应对分类等任务时可以更好的学习本质特征。不过当需要感知位置信息时，传统卷积就有点力不从心了。为了使得卷积能够感知空间信息，在输入 feature map 后面增加了两个 coordinate 通道，分别表示原始输入的 x 和 y 坐标，然后再进行传统卷积，从而使得卷积过程可以感知 feature map 的空间信息

在训练神经网络时，没有直接在后向传播中使用，只是训练时输入该座标信息，使得网络可以根据不同任务需求学习平移不变性或者一定程度的平移依赖性

ins_feat = x # 当前实例特征tensor
# 生成从-1到1的线性值
x_range = torch.linspace(-1, 1, ins_feat.shape[-1], device=ins_feat.device)
y_range = torch.linspace(-1, 1, ins_feat.shape[-2], device=ins_feat.device)
y, x = torch.meshgrid(y_range, x_range) # 生成二维坐标网格
y = y.expand([ins_feat.shape[0], 1, -1, -1]) # 扩充到和ins_feat相同维度
x = x.expand([ins_feat.shape[0], 1, -1, -1])
coord_feat = torch.cat([x, y], 1) # 位置特征
ins_feat = torch.cat([ins_feat, coord_feat], 1) # concatnate一起作为下一个卷积的输入

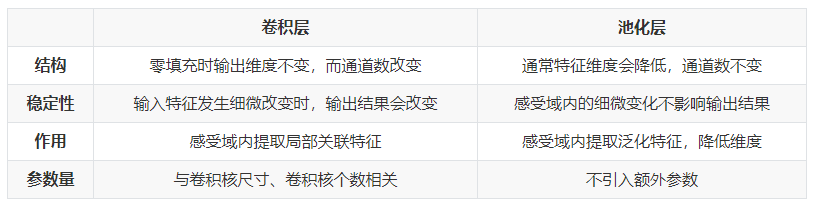
卷积层和池化层有什么区别？

卷积层核池化层在结构上具有一定的相似性，都是对感受域内的特征进行提取，并且根据步长设置获取到不同维度的输出，但是其内在操作是有本质区别的

每层卷积是否只能用一种尺寸的卷积核？

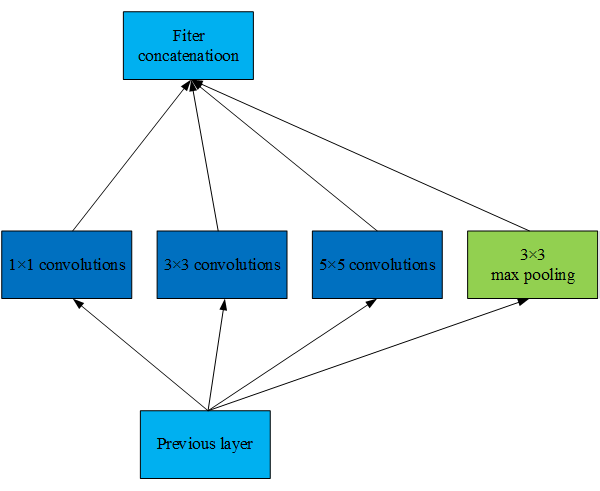
经典的神经网络一般都属于层叠式网络，每层仅用一个尺寸的卷积核，如VGG结构中使用了大量的3×3卷积层。事实上，同一层特征图可以分别使用多个不同尺寸的卷积核，以获得不同尺度的特征，再把这些特征结合起来，得到的特征往往比使用单一卷积核的要好
如GoogLeNet、Inception系列的网络，均是每层使用了多个卷积核结构。如图所示，输入的特征在同一层分别经过1×1、3×3和5×5三种不同尺寸的卷积核，再将分别得到的特征进行整合，得到的新特征可以看作不同感受域提取的特征组合，相比于单一卷积核会有更强的表达能力

怎样才能减少卷积层参数量？

使用堆叠小卷积核代替大卷积核：VGG网络中2个3x3的卷积核可以代替1个5x5的卷积核
使用分解卷积操作：将原本 KxKxC 的卷积操作分离为 KxKx1和1x1xC 的两部分操作
添加1x1的卷积操作：与分离卷积类似，但是通道数可变，在KxKxC_1卷积前添加1x1xC_2的卷积核（满足C_2
在卷积层前使用池化操作：池化可以降低卷积层的输入特征维度

采用宽卷积的好处有什么？

宽卷积对应的是窄卷积，实际上并不是卷积操作的类型，指的是卷积过程中的填充方法，对应的是’SAME’填充和’VALID’填充。
SAME填充：采用零填充的方式对卷积核不满足整除条件的输入特征进行补全，以使卷积层的输出维度保持与输入特征维度一致；
VALID填充：实际并不进行任何填充，在输入特征边缘位置若不足以进行卷积操作，则对边缘信息进行舍弃，因此在步长为1的情况下该填充方式的卷积层输出特征维度可能会略小于输入特征的维度
左部分为窄卷积。注意到越在边缘的位置被卷积的次数越少。宽卷积可以看作在卷积之前在边缘用0补充，常见有两种情况，一个是全补充，如图右部分，这样输出大于输入的维度

全连接、局部连接、全卷积与局部卷积？

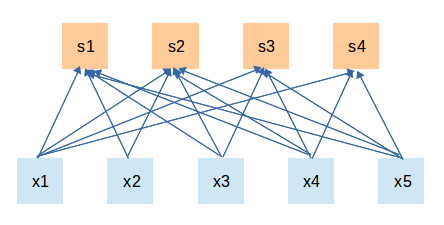
全连接： 层间神经元完全连接，每个输出神经元可以获取到所有输入神经元的信息，有利于信息汇总，常置于网络末层；连接与连接之间独立参数，大量的连接大大增加模型的参数规模
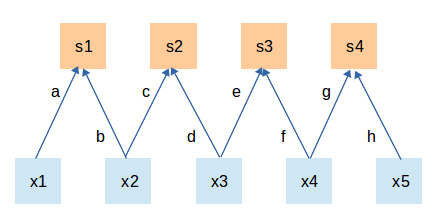
局部连接： 层间神经元只有局部范围内的连接，在这个范围内采用全连接的方式，超过这个范围的神经元则没有连接；连接与连接之间独立参数，相比于全连接减少了感受域外的连接，有效减少参数规模
全卷积： 层间神经元只有局部范围内的连接，在这个范围内采用全连接的方式，连接所采用的参数在不同感受域之间共享，有利于提取特定模式的特征；相比于局部连接，共用感受域之间的参数可以进一步减少参数量
局部卷积： 层间神经元只有局部范围内的连接，感受域内采用全连接的方式，而感受域之间间隔采用局部连接与全卷积的连接方式；相比与全卷积成倍引入额外参数，但有更强的灵活性和表达能力；相比于局部连接，可以有效控制参数量

局部卷积的应用?

并不是所有的卷积都会进行权重共享，在某些特定任务中，会使用不权重共享的卷积。下面通过人脸这一任务来进行讲解。在读人脸方向的一些paper时，会发现很多都会在最后加入一个Local Connected Conv，也就是不进行权重共享的卷积层
参数不共享原因：（1）对齐的人脸图片中，不同的区域会有不同的统计特征，因此并不存在特征的局部稳定性，所以使用相同的卷积核会导致信息的丢失；（2）不共享的卷积核并不增加 inference 时特征的计算量，仅会增加训练时的计算量。使用不共享的卷积核，由于需要训练的参数量大大增加，因此往往需要通过其他方法增加数据量

为捕获 featrue map 上长距离的依赖，CNN 有哪些方法？

CNN 设计特性导致其天然视野受限，这对复杂场景的识别带来困难，常常通过其他方法显式构建像素之间的依赖关系，避免这个问题。目前为之，一共有 3 个方法可以做到
Query 依赖 (自注意力机制)：对于 HxW 大小的特征，构建 HWxHW 的自注意力矩阵，Non-local、transformer 等模型使用该方法
无 Query 依赖（上下文依赖）: 在 CNN 使用全局池化生成通道注意力、使用 1 x 1 卷积生成空间注意力，然后使用网络去学习这种依赖
CRF：deeplabv1、deeplabv2 使用该方法后处理模型输出，迭代构建像素之间的远程依赖

在 CNN 架构设计上，经常修改哪些指标去提升网络性能？

网络的宽度 width：每层卷积的输出通道数
网络的深度 depth：网络的层数
网络的分辨率 resolution：输入图像的分辨率大小
网络的增长率 growth：随着层数的增加，每层卷积输出通道数的增长比例
网络的特征复用：如 DenseNet 可以使用更浅的网络，更少的参数，提升特征复用，达到与深度网络相当的性能
高效特征融合：InceptionNet的split-transforms-merge模式，将输入分别使用不同的转换分支提取特征，然后将多个分支的结果进行合并实现特征融合