图卷积网络 - GCN

GCN 的基础知识

1. GCN 的基本概念与用途

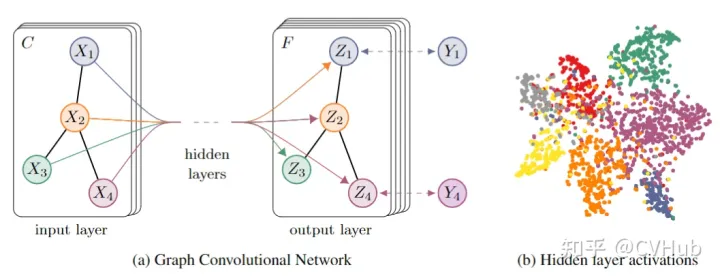
图卷积神经网络（Graph Convolutional Network, GCN）是一种用于处理图数据的深度学习模型。它通过利用边的信息对节点信息进行聚合，从而生成新的节点表示。GCN 可以应用于多种任务，包括但不限于：

• 节点分类：预测特定节点的类型。
• 链接预测：预测两个节点是否有联系。
• 社区检测：识别密集联系的节点群落。
• 网络相似性：评估两个（子）网络之间的相似度。

2. GCN 的原理

从空域角度来看，图卷积是一个消息传递（Message Passing）的过程。具体来说：

• 传播：每个节点将自身的特征信息发送给相邻的邻居节点。
• 聚合：每个节点将接收到的信息进行汇总，并通过非线性变换生成新的表示。

GCN 的核心思想是利用边的信息对节点信息进行聚合，从而生成新的节点表示。这种过程可以类比于 CNN 中的卷积操作，就是一个特征提取器，只不过它的对象是图数据，直觉上，训练时的每个 GCN 层中，对于每个节点，用线性权重和非线性转换邻居的表达向量，相当于收集邻居的信息，通过多层的 GCN，可以收集 “邻居 - 邻居 -…” 的信息

3. GCN 网络结构分析

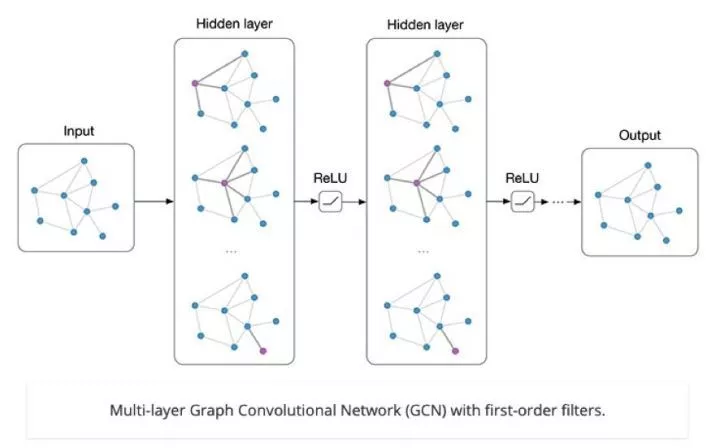
GCN 的每一层通过以下步骤实现：

1. 邻接矩阵和特征矩阵相乘：首先将每个顶点的邻居特征进行汇总。
2. 参数矩阵加激活函数：然后，对汇总后的特征进行线性变换，并加上一个非线性激活函数。

具体公式如下：

$$H^{(l+1)}=\sigma ((D^{-\frac 1 2}AD^{-\frac 1 2})H^{(l)}W^{(l)})$$

• $H^{(l)}$ 是第$l$ 层的节点特征矩阵
• $W^{(l)}$ 是权重矩阵
• $\sigma$ 是激活函数，通常使用 ReLU、Sigmoid 等非线性激活函数
• A 是邻接矩阵，是一个二阶张量，其中$A_{ij}=1$ 表示节点 i 与节点 j 之间有边连接，否则为 0
• D 是度矩阵，是一个对角矩阵，其中对角线元素是邻接矩阵每一行的非零元素只和，即$D_{ij}=\sum_j A_{ij}$
• $D^{-\frac 1 2}$：对角矩阵  的元素取倒数的平方根。具体来说，如果$D_{ii}=d_i$，则$D_{ii}^{-\frac 1 2}=\frac 1 {\sqrt d_i}$
• $D^{-\frac 1 2}AD^{-\frac 1 2}$：是归一化的拉普拉斯矩阵（Normalized Laplacian Matrix）。这个操作可以看作是对邻接矩阵进行归一化，使得每个节点的特征向量在传播时能够更好地考虑其邻居的信息

示例：
假设我们有一个简单的图，包含两个节点和一条边。邻接矩阵 (A) 和度矩阵 (D) 如下：

$$A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}, \quad D = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$

假设初始节点特征矩阵 $H^{(0)}$ 和权重矩阵 $W^{(0)}$ 如下：

$$H^{(0)} = \begin{bmatrix} h_1^{(0)} \\ h_2^{(0)} \end{bmatrix}, \quad W^{(0)} = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix}$$

计算归一化后的拉普拉斯矩阵：

$$D^{-\frac{1}{2}} A D^{-\frac{1}{2}} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$$

然后进行线性变换和聚合：

$$(D^{-\frac{1}{2}} A D^{-\frac{1}{2}}) H^{(0)} W^{(0)} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} h_1^{(0)} \\ h_2^{(0)} \end{bmatrix} \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix} = \begin{bmatrix} h_2^{(0)} W \\ h_1^{(0)} W \end{bmatrix}$$

最后，通过激活函数得到新的节点特征矩阵：

$$H^{(1)} = \sigma \left( (D^{-\frac{1}{2}} A D^{-\frac{1}{2}}) H^{(0)} W^{(0)} \right)$$

4. 代码示例

GCN 网络结构可以表示为多层的图卷积操作。每一层通过以下步骤实现：

1. 输入层：接收节点特征和邻接矩阵。
2. 隐藏层：进行多次图卷积操作，每层都包含线性变换和非线性激活函数。
3. 输出层：最终生成节点的表示或分类结果。

以下是一个简单的 GCN 模型实现示例：

import torch
from torch_geometric.nn import GCNConv

class GCN(torch.nn.Module):
    def __init__(self, in_channels, out_channels):
        super(GCN, self).__init__()
        self.conv1 = GCNConv(in_channels, 16)
        self.conv2 = GCNConv(16, out_channels)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index

        # First convolution
        x = self.conv1(x, edge_index)
        x = torch.nn.functional.relu(x)
        x = torch.nn.functional.dropout(x, training=self.training)

        # Second convolution
        x = self.conv2(x, edge_index)
        
        return x

5. 总结

GCN 具有以下特点：

• 多层结构：通过叠加多个图卷积层，可以实现对多阶邻域信息的捕捉。
• 结合属性和结构：不仅利用节点的属性信息，还考虑了节点之间的关系（边）。
• 灵活性高：可以通过调整层数、激活函数等参数来适应不同的任务需求。

GCN 是一种强大的图数据处理工具，通过结合节点属性和边信息，可以有效地进行节点分类、链接预测等任务。其多层结构和灵活性使其在许多实际应用中表现出色。

参考：

1. https://blog.csdn.net/fs1341825137/article/details/109783308