随机梯度下降 - SGD

发表于 更新于 分类于 ， 阅读次数： 本文字数： 4.2k 阅读时长 ≈ 4 分钟

什么是随机梯度下降？

  • 一种简单但非常有效的拟合线性模型的方法。当样本数量（和特征数量）非常大时，它特别有用
  • 这些类 SGDClassifier 并 SGDRegressor 提供了使用不同（凸）损失函数和不同惩罚来拟合用于分类和回归的线性模型的功能。例如，与 loss=“log”，SGDClassifier 拟合逻辑回归模型，而与 loss="hinge" 它拟合线性支持向量机（SVM)
  • 严格来说，SGD 只是一种优化技术，并不对应于特定的机器学习模型家族。这只是训练模型的一种 方式
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
     >>> from sklearn.linear_model import SGDClassifier
     >>> X = [[0., 0.], [1., 1.]]
     >>> y = [0, 1]
     >>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
     >>> clf.fit(X, y)
    SGDClassifier(max_iter=5)
     >>> clf.predict([[2., 2.]])
    array([1])
     >>> clf.coef_ # 模型参数
    array([[9.9..., 9.9...]])
     >>> clf.intercept_ # 偏移或偏差
    array([-9.9...])

随机梯度下降的实用技巧？

  • 对特征缩放很敏感，因此强烈建议对数据进行缩放。例如，将输入向量 X 上的每个属性缩放为 [0,1] 或 [-1,+1]，或将其标准化为均值 0 和方差 1

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    from sklearn.preprocessing import StandardScaler
    scaler = StandardScaler()
    scaler.fit(X_train)  # Don't cheat - fit only on training data
    X_train = scaler.transform(X_train)
    X_test = scaler.transform(X_test)  # apply same transformation to test data

    # Or better yet: use a pipeline!
    from sklearn.pipeline import make_pipeline
    est = make_pipeline(StandardScaler(), SGDClassifier())
    est.fit(X_train)
    est.predict(X_test)

  • 找到一个合理的正则化项 α 最好使用自动超参数搜索来完成

什么是随机梯度下降 (SGD)?

  • 随机梯度下降（SGD）是一种简单而高效的方法，用于在凸损失函数下拟合线性分类器和回归器，如（线性）支持向量机和 Logistic 回归。尽管 SGD 在机器学习界已经存在了很长时间，但在大规模学习的背景下，它最近才受到了相当多的关注
  • 严格来说，SGD 只是一种优化技术，并不对应于一个特定的机器学习模型系列。它只是一种训练模型的方法

scikit-learn 中 ** 随机梯度下降 (SGD)** 分类方法 SGDClassifier 的使用？

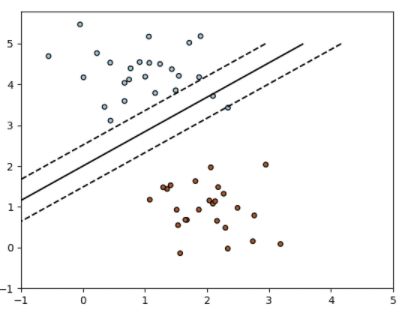
  • SGDClassifier 类实现了一个普通的随机梯度下降学习程序，它支持不同的损失函数和分类惩罚。下面是一个用铰链损失训练的 SGDClassifier 的决策边界 (decisionboundary)，相当于一个线性 SVM
  • 与其他分类器一样，SGD 必须与两个数组相配合：一个形状为 X 的数组（n_samples, n_features），存放训练样本；一个形状为 Y 的数组（n_samples,），存放训练样本的目标值（类标签）
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
     >>> from sklearn.linear_model import SGDClassifier
     >>> X = [[0., 0.], [1., 1.]]
     >>> y = [0, 1]
     >>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
     >>> clf.fit(X, y)
    SGDClassifier(max_iter=5)
    # 预测数据
     >>> clf.predict([[2., 2.]])
    array([1])
     >>> clf.coef_
    array([[9.9..., 9.9...]])
    # 偏移
     >>> clf.intercept_
    array([-9.9...])
    # 到超平面的有符号距离
     >>> clf.decision_function([[2., 2.]])
    array([29.6...])

scikit-learn 中 ** 随机梯度下降 (SGD)** 分类方法 SGDClassifier 支持的损失函数？

  • 合页损失 (铰链损失) (hinge loss)
  • huber loss
  • 逻辑斯谛损失 (Logistic Loss)

scikit-learn 中 ** 随机梯度下降 (SGD)** 分类方法 SGDClassifier 的参数惩罚？

  • penalty=“l2”。对 coef_的 L2 准则惩罚。
  • penalty=“l1”: 对 coef_的 L1 规范惩罚。
  • penalty=“elasticnet”。L2 和 L1 的凸形组合；(1 - l1_ratio) * L2 + l1_ratio * L1
  • 默认设置是 punice=“l2”。L1 惩罚会导致稀疏的解决方案，使大多数系数为零。弹性网 11 解决了 L1 惩罚在高度相关的属性中的一些缺陷

scikit-learn 中 ** 随机梯度下降 (SGD)** 分类方法 SGDClassifier 如何实现多分类？

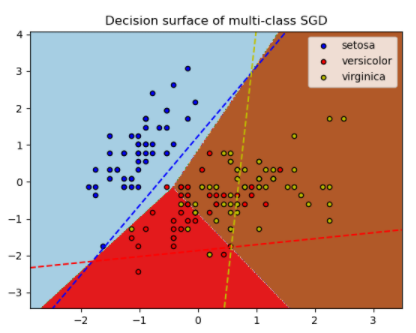
  • 下图说明了虹膜数据集上的 OVA 方法。虚线代表三个 OVA 分类器；背景颜色显示了由三个分类器引起的决策面
  • SGDClassifier 通过将多个二元分类器以 “一个对所有”（OVA）的方案结合起来支持多类分类。对于每一个 K 类，都要学习一个二进制分类器，以区分该类和所有其他 K-1 类。在测试时，我们计算每个分类器的置信度分数（即到超平面的有符号距离），并选择具有最高置信度的类别
  • SGDClassifier 通过 fit 参数 class_weight 和 sample_weight 支持加权的类和加权的实例

scikit-learn 中 ** 随机梯度下降 (SGD)** 分类方法 SGDRegressor 的使用？

  • 1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    >>> import numpy as np
    >>> from sklearn.linear_model import SGDRegressor
    >>> from sklearn.pipeline import make_pipeline
    >>> from sklearn.preprocessing import StandardScaler
    >>> n_samples, n_features = 10, 5
    >>> rng = np.random.RandomState(0)
    >>> y = rng.randn(n_samples)
    >>> X = rng.randn(n_samples, n_features)
    >>> # Always scale the input. The most convenient way is to use a pipeline.
    >>> reg = make_pipeline(StandardScaler(),
    ...                     SGDRegressor(max_iter=1000, tol=1e-3))
    >>> reg.fit(X, y)
    Pipeline(steps=[('standardscaler', StandardScaler()),
    				('sgdregressor', SGDRegressor())])

scikit-learn 中 ** 随机梯度下降 (SGD)** 分类方法 SGDRegressor 支持的损失函数？

  • 平方损失 (MSELoss/L2Loss)
  • huber loss

** 随机梯度下降 (SGD)** 的使用技巧？

  • 随机梯度下降法对特征的缩放很敏感，所以强烈建议对你的数据进行缩放。例如，将输入向量 X 上的每个属性缩放为 [0,1] 或 [-1,+1]，或将其标准化为均值 0 和方差 1。注意，同样的比例必须应用于测试向量以获得有意义的结果
  • 寻找合理的正则化 (regularization) 项 α 最好使用自动超参数搜索，例如 GridSearchCV 或 RandomizedSearchCV，通常在 10.0**-np.arange (1,7) 范围内进行

** 随机梯度下降 (SGD)** 的数学描述？

  • 给出一组训练实例(x1,y1),…,(xn,yn)(x_1, y_1), \ldots, (x_n, y_n)，其中xi∈Rmx_i \in \mathbf{R}^m 和yi∈Ry_i \in \mathcal{R}(yi∈−1,1y_i \in {-1, 1} 为分类），我们的目标是学习一个线性评分函数f(x)=wTx+bf(x) = w^T x + b，模型参数为w∈Rmw \in \mathbf{R}^m 和截距b∈Rb \in \mathbf{R}。为了对二元分类进行预测，我们只需看f(x)f(x) 的符号。为了找到模型参数，我们使正则化训练误差小化，其公式

E(w,b)=1n∑i=1nL(yi,f(xi))+αR(w)E(w,b) = \frac{1}{n}\sum_{i=1}^{n} L(y_i, f(x_i)) + \alpha R(w)

  • 其中 L 是衡量模型（错误）拟合的损失函数，R 是惩罚模型复杂性的正则化项（又称惩罚）；α>0 是控制正则化强度的非负超参数