高斯过程

什么是高斯过程？

• 高斯过程（GP）是一种通用的监督学习方法，旨在解决回归和概率分类问题
• 

高斯过程的回归任务如何实现？

• GaussianProcessRegressor 为回归目的实现了高斯过程（GP）。为此，需要指定 GP 的先验。先验均值被假定为常数和零（normalize_y=False）或训练数据的均值（normalize_y=True）。先验的协方差是通过传递一个核对象来指定的
• 目标中的噪声水平可以通过参数 alpha 来指定，可以是全局的标量，也可以是每个数据点。请注意，适度的噪声水平也有助于在拟合过程中处理数字问题，因为它可以有效地实现 Tikhonov (吉洪诺夫) 正则化，即通过将其添加到内核矩阵的对角线上。 明确指定噪声水平的另一种方法是在核中加入 WhiteKernel 组件，它可以从数据中估计全局噪声水平

   >>> from sklearn.datasets import make_friedman2
   >>> from sklearn.gaussian_process import GaussianProcessRegressor
   >>> from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel
   >>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0)
   >>> kernel = DotProduct() + WhiteKernel()
   >>> gpr = GaussianProcessRegressor(kernel=kernel,
  ...         random_state=0).fit(X, y)
   >>> gpr.score(X, y)
  0.3680...
   >>> gpr.predict(X[:2,:], return_std=True)
  (array([653.0..., 592.1...]), array([316.6..., 316.6...])) 

高斯回归与岭回归比较？

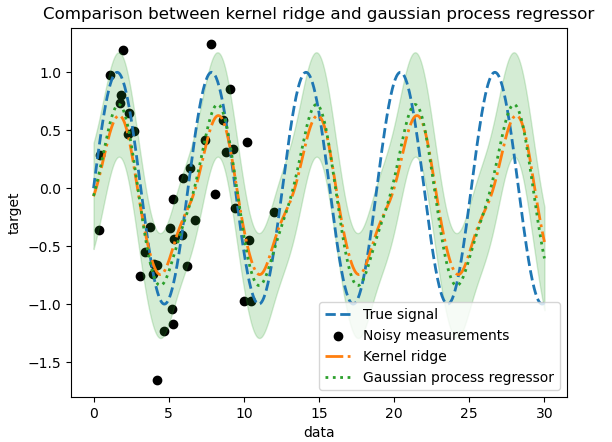
• 核脊回归（KRR）和 GPR 都是通过内部采用 "内核技巧" 来学习目标函数。KRR 在各自内核诱导的空间中学习一个线性函数，该函数对应于原始空间中的一个非线性函数。核空间中的线性函数是根据平均平方误差损失和山脊正则化来选择的。GPR 使用核来定义目标函数的先验分布的协方差，并使用观察到的训练数据来定义似然函数。基于贝叶斯定理，定义了目标函数的（高斯）后验分布，其平均值被用于预测
• 
• 两种方法都学习了目标函数的合理模型。GPR 正确地识别了函数的周期性，大约是 2∗π（6.28），而 KRR 选择了加倍的周期性 4∗π。除此之外，GPR 还提供了合理的预测置信度界限，这是 KRR 所没有的。这两种方法的一个主要区别是拟合和预测所需的时间：虽然 KRR 的拟合原则上很快，但超参数优化的网格搜索会随着超参数数量的增加而呈指数增长（“维度诅咒”）。GPR 中基于梯度的参数优化不会受到这种指数扩展的影响，因此在这个具有 3 维超参数空间的例子中速度要快得多

高斯过程的分类任务如何实现？

• GaussianProcessClassifier 为分类目的实现了高斯过程（GP），更确切地说，是用于概率分类，其中测试预测采取类概率的形式

   >>> from sklearn.datasets import load_iris
   >>> from sklearn.gaussian_process import GaussianProcessClassifier
   >>> from sklearn.gaussian_process.kernels import RBF
   >>> X, y = load_iris(return_X_y=True)
   >>> kernel = 1.0 * RBF(1.0)
   >>> gpc = GaussianProcessClassifier(kernel=kernel,
  ...         random_state=0).fit(X, y)
   >>> gpc.score(X, y)
  0.9866...
   >>> gpc.predict_proba(X[:2,:])
  array([[0.83548752, 0.03228706, 0.13222543],
  	   [0.79064206, 0.06525643, 0.14410151]])

什么是高斯过程内核？

• 核（在 GPs 中也称为 “协方差函数”）是 GP 的一个关键成分，它决定了 GP 的先验和后验的形状。它们通过定义两个数据点的 "相似性" 和相似数据点应具有相似目标值的假设，对正在学习的函数的假设进行编码。可以区分两类内核：静止的内核只取决于两个数据点的距离，而不取决于它们的绝对值，因此对输入空间的平移是不变的，而非静止的内核也依赖于数据点的具体数值。静态核可以进一步细分为各向同性和各向异性核，其中各向同性核对输入空间的旋转也是不变的

高斯过程有哪些内核？

• 高斯过程的基本内核
• 高斯过程的空白核 (WhiteKernel)
• 高斯过程的 Radial-basis function (RBF) 核
• 高斯过程的 Matérn 核
• 高斯过程的 Rational quadratic kernel 核
• 高斯过程的 Exp-Sine-Squared 核
• 高斯过程的 Dot-Product 核

如何理解高斯过程的基本内核？

• ConstantKernel 内核可以作为 Product 内核的一部分，它可以缩放其他因子（内核）的大小，或者作为 Sum 内核的一部分，它可以修改高斯过程的平均值。它取决于一个参数 constant_value

• $$k(x_i, x_j) = constant\_value \;\forall\; x_1, x_2$$

如何理解高斯过程的空白核 (WhiteKernel)？

• 白核（WhiteKernel）的主要用途是作为和核的一部分，解释信号的噪声成分。调整其参数 noise_level 对应于估计噪音水平

• $$k(x_i, x_j) = noise\_level \text{ if } x_i == x_j \text{ else } 0$$

如何理解高斯过程的 Radial-basis function (RBF) 核？

• RBF 核是一个静止的核。它也被称为 "平方指数" 核。它的参数是一个长度尺度参数 l>0，它可以是一个标量（各向同性的核的变体），也可以是一个与输入 x 具有相同维数的矢量（各向异性的核的变体）, 其中 d (⋅,⋅) 为欧几里得距离

• $$k(x_i, x_j) = \text{exp}\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)$$

如何理解高斯过程的 Matérn 核？

• Matern 核是一个静止的核，是高斯过程的 Radial-basis function (RBF) 核的泛化。它有一个额外的参数 ν，控制所产生的函数的平滑度。它的参数是一个长度尺度参数 l>0，可以是一个标量（各向同性的核的变体），也可以是一个与输入 x 相同维数的向量（各向异性的核的变体）， 其中 d (⋅,⋅) 为欧氏距离 (L2 距离)，Kν(⋅) 是一个修正的贝塞尔函数，Γ(⋅) 是伽马函数

• $$k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)^\nu K_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg),$$

如何理解高斯过程的 Rational quadratic kernel 核？

• RationalQuadratic 核可以被看作是具有不同特征长度尺度的 RBF 核的尺度混合物（一个无限的和）。它的参数是长度尺度参数 l>0 和尺度混合参数 α>0，目前只支持 l 是标量的各向同性变体

• $$k(x_i, x_j) = \left(1 + \frac{d(x_i, x_j)^2}{2\alpha l^2}\right)^{-\alpha}$$

如何理解高斯过程的 Exp-Sine-Squared 核？

• ExpSineSquared 核允许对周期函数进行建模。它的参数是长度尺度参数 l>0 和周期性参数 p>0。目前只支持 l 是标量的各向同性变量

• $$k(x_i, x_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x_i, x_j) / p) }{ l^ 2} \right)$$

如何理解高斯过程的 Dot-Product 核？

• DotProduct 核是非平稳的，可以从线性回归中得到，将 N (0,1) 个预设值放在$x_d (d = 1, … , D)$ 的系数，加上一个$N(0, \sigma_0^2)$ 的偏置，DotProduct 核对坐标围绕原点的旋转是不变的，但对平移是不变的。

• $$k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j$$