线性代数 - 标量、向量、矩阵、张量

发表于 2016-11-09 更新于 2025-01-18 分类于 0-数学基础， B-线性代数阅读次数：本文字数： 11k 阅读时长 ≈ 10 分钟

本文从标量、向量入手，讲解到矩阵、张量，并讲解了矩阵与张量的运算规则，对于神经网络来说，张量之间更多的是：矩阵相乘 (卷积提取特征)、矩阵内积 (transformer 计算自注意力)

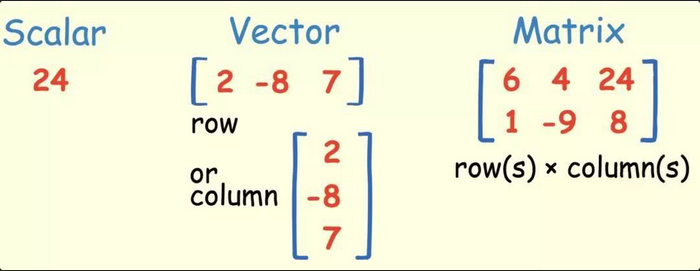
什么是标量 (scalar)？

一个标量表示一个单独的数

>>> x=torch.tensor([3.0])
>>> y=torch.tensor([2.0])
>>> x+y,x*y,x/y,x**y
(tensor([5.]), tensor([6.]), tensor([1.5000]), tensor([9.]))

什么是向量 (vector)？

由标量 (scalar) 组成的列表，标量值称为向量的元素或分量
通常赋予向量粗体的小写变量名称，比如 xx。向量中的元素可以通过带脚标的斜体表示。向量 $X$ $X$ 的第一个元素是 $X_1$ $X_{1}$ ，第二个元素是 $X_2$ $X_{2}$
1
2
3
4
5
6
7
8
9
10
11
12
13
>>> x=torch.arange(6)
>>> x
tensor([0, 1, 2, 3, 4, 5])

# 使用下标访问
>>> x[3:]
tensor([3, 4, 5])

# 获取向量属性
>>> len(x)
6
>>> x.shape
torch.Size([6])

什么是矩阵 (matrix)？

向量 (vector) 将标量 (scalar) 从零阶推广到一阶，矩阵将向量从一阶推广到二阶

>>> import torch
>>> torch.arange(20).reshape(5,4)
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])

什么是张量 (tensor)?

就像向量 (vector) 是标量 (scalar) 的推广，矩阵 (matrix) 是向量的推广一样，张量指具有任意数量轴的 n 维数组的通用方法

>>> import torch
>>> A=torch.arange(20).reshape(5,4)
>>> B=A.clone()
>>> A+B
tensor([[ 0,  2,  4,  6],
        [ 8, 10, 12, 14],
        [16, 18, 20, 22],
        [24, 26, 28, 30],
        [32, 34, 36, 38]])

标量、向量、矩阵、张量之间的关系？

标量 (scalar) 是 0 阶张量，向量 (vector) 是一阶张量，矩阵 (matrix) 是二阶张量
标量就是知道棍子的长度，但是你不会知道棍子指向哪儿
向量就是不但知道棍子的长度，还知道棍子指向前面还是后面
张量就是不但知道棍子的长度，也知道棍子指向前面还是后面，还能知道这棍子又向上 / 下和左 / 右偏转了多少

向量的数乘？

一个数乘以向量中的每个元素 $2 \times\left(\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right)=\left(\begin{array}{l} 2 \\ 4 \\ 6 \end{array}\right)$

向量的内积 (点积、数量积、标量积、dot product)?

又称数量积或标量积，是一种接受两个等长的数字序列（通常是坐标向量）、返回单个数字的代数运算

\left(\begin{array}{lll} 0 & 1 & 2 & 3 \end{array}\right)\left(\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}\right)=0 \times 1+1 \times 1+2 \times 1+3 \times 1=6

>>> import torch
>>> x=torch.arange(4,dtype=torch.float)
>>> y=torch.ones(4,dtype=torch.float32)
>>> x,y,torch.dot(x,y)
(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
# torch.dot应用非1D张量上会报错
>>> x,y=torch.arange(6).reshape(3,2),torch.ones(2).reshape(2,1)
>>> x,y,torch.dot(x,y)
Traceback (most recent call last):
  File "", line 1, in 
RuntimeError: 1D tensors expected, but got 2D and 2D tensors

向量的外积 (叉积、叉乘、向量积)？

与点积不同，它的运算结果是向量，并且两个向量的叉积与这两个向量组成的坐标平面垂直
对于 2 个向量， $a=\left(x_{1}, y_{1}, z_{1}\right),b=\left(x_{2}, y_{2,} z_{2}\right)$ ，外积如下，其中 $i=(1,0,0) \quad \mathrm{j}=(0,1,0) \quad \mathrm{k}=(0,0,1)$
$a \times b=\left|\begin{array}{lll} \mathrm{i} & \mathrm{j} & \mathrm{k} \\ x_{1} & y_{1} & z_{1} \\ x_{2} & y_{2} & z_{2} \end{array}\right|=\left(y_{1} z_{2}-y_{2} z_{1},-\left(x_{1} z_{2}-x_{2} z_{1}\right), x_{1} y_{2}-x_{2} y_{1}\right)$
在三维几何中，向量 a 和向量 b 的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于 a 和 b 向量构成的平面；如果两个向量方向相同或相反（即它们没有线性无关的分量），亦或任意一个的长度为零，那么它们的外积为零

矩阵的数乘？

用一个数乘以矩阵中的每个元素 $5 \times\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 0 & 0 \end{array}\right]=\left[\begin{array}{ccc} 5 & 10 & 15 \\ 0 & 0 & 0 \end{array}\right]$

矩阵和向量相乘？

矩阵和向量相乘表示对矩阵进行遍历求和

>>> A,x=torch.arange(20,dtype=torch.float32).reshape(5,4),torch.ones(4,dtype=torch.float32)
>>> A
tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [12., 13., 14., 15.],
        [16., 17., 18., 19.]])
>>> x
tensor([1., 1., 1., 1.])
>>> A.shape,x.shape,torch.mv(A,x)
(torch.Size([5, 4]), torch.Size([4]), tensor([ 6., 22., 38., 54., 70.]))

矩阵之间的乘法？

线性代数里面的矩阵乘法，要求第一个矩阵的列数和第二个矩阵的行数相等 $C=A B=\left(\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right)\left(\begin{array}{ll} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{array}\right)=\left(\begin{array}{ll} 1 \times 1+2 \times 2+3 \times 3 & 1 \times 4+2 \times 5+3 \times 6 \\ 4 \times 1+5 \times 2+6 \times 3 & 4 \times 4+5 \times 5+6 \times 6 \end{array}\right)=\left(\begin{array}{ll} 14 & 32 \\ 32 & 77 \end{array}\right)$

矩阵之间的哈达玛积 (Hadamard product)?

两个相乘的矩阵维度一致，逐元素相乘（矩阵点乘）

>>> import torch
>>> A=torch.arange(20).reshape(5,4)
>>> A
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])
>>> B=A.clone()
>>> A*B
tensor([[  0,   1,   4,   9],
        [ 16,  25,  36,  49],
        [ 64,  81, 100, 121],
        [144, 169, 196, 225],
        [256, 289, 324, 361]])

矩阵之间的克罗内克积 (Kronecker product)？

两个任意大小的矩阵间的运算，被称为直积或张量积 $\left[\begin{array}{ll} 1 & 2 \\ 3 & 1 \end{array}\right] \otimes\left[\begin{array}{ll} 0 & 3 \\ 2 & 1 \end{array}\right]=\left[\begin{array}{llll} 1 \cdot 0 & 1 \cdot 3 & 2 \cdot 0 & 2 \cdot 3 \\ 1 \cdot 2 & 1 \cdot 1 & 2 \cdot 2 & 2 \cdot 1 \\ 3 \cdot 0 & 3 \cdot 3 & 1 \cdot 0 & 1 \cdot 3 \\ 3 \cdot 2 & 3 \cdot 1 & 1 \cdot 2 & 1 \cdot 1 \end{array}\right]=\left[\begin{array}{llll} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 3 \\ 6 & 3 & 2 & 1 \end{array}\right]$

什么是方程组？

形式如下：
$\left\{\begin{array}{l} 2 x-y=0 \\ -4 x+2 y=0 \end{array}\right.$
把方程组中所有系数写到了一个矩阵 (matrix) 里面，把所有未知数写到第二个框里，把所有等式右边的值写到第三个框里
$\left[\begin{array}{cc} 2 & -1 \\ -4 & 2 \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \end{array}\right]$
增广矩阵：将上面内容矩阵形式改为增广矩阵
$\left[\begin{array}{cc|c} 2 & -1 & 0 \\ -4 & 2 & 0 \end{array}\right]$
方程组的等式右边全为 0 的方程组为齐次线性方程组，否则为非齐次线性方程组

方程组的初等变换？

现有方程组
$\left\{\begin{array}{l} x+2 y+z=2 \\ 3 x+8 y+z=12 \\ 4 y+z=2 \end{array}\right.$
表示为增广矩阵
$\left[\begin{array}{cccc} 1 & 2 & 1 & 2 \\ 3 & 8 & 1 & 12 \\ 0 & 4 & 1 & 2 \end{array}\right]$
消除 (2,1) 位置的元素，通过 $\text { Row } 2=\operatorname{Row} 2+\operatorname{Row} 1 \times(-3)$ , 得
$\left[\begin{array}{cccc} \frac{1}{3} & 2 & 1 & 2 \\ 3 & 8 & 1 & 12 \\ 0 & 4 & 1 & 2 \end{array}\right] \stackrel{(2,1)}{\rightarrow}\left[\begin{array}{cccc} 1 & 2 & 1 & 2 \\ 0 & 2 & -2 & 6 \\ 0 & 4 & 1 & 2 \end{array}\right]$
消除 (3,2) 位置的元素，通过 $\text { Row3 }=\text { Row3 }+\text { Row } 2 \times(-2)$ , 得
$\left[\begin{array}{cccc} 1 & 2 & 1 & 2 \\ 0 & \frac{2}{4} & -2 & 6 \\ 0 & 4 & 1 & 2 \end{array}\right] \stackrel{(3,2)}{\rightarrow}\left[\begin{array}{cccc} 1 & 2 & 1 & 2 \\ 0 & 2 & -2 & 6 \\ 0 & 0 & 5 & -10 \end{array}\right]$
消元后的矩阵等式为
$\left[\begin{array}{ccc} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 0 & 5 \end{array}\right]\left[\begin{array}{c} x \\ y \\ z \end{array}\right]=\left[\begin{array}{c} 2 \\ 6 \\ -10 \end{array}\right]$
解得， $x=2,y=1,z=-2$

什么是范数？

在线性代数中，向量范数是将向量映射到标量的函数 f

>>> u=torch.tensor([3.0,4.0])
# L1范数
>>> torch.abs(u).sum()
tensor(7.)
# L2范数
>>> torch.norm(u)
tensor(5.)

一个向量的范数告诉我们一个向量有多大。这里考虑的大小（size）概念不涉及维度，而是分量的大小

向量范数的归纳？

定义一个向量为： $\vec{a}=[-5, 6, 8, -10]$ 。任意一组向量设为 $\vec{x}=(x_1,x_2,…,x_N)$ 。其不同范数求解如下
向量的 1 范数：向量的各个元素的绝对值之和，上述向量 $\vec{a}$ 的 1 范数结果就是：29
$\Vert\vec{x}\Vert_1=\sum_{i=1}^N\vert{x_i}\vert$
向量的 2 范数：向量的每个元素的平方和再开平方根，上述 $\vec{a}$ 的 2 范数结果就是：15
$\Vert\vec{x}\Vert_2=\sqrt{\sum_{i=1}^N{\vert{x_i}\vert}^2}$
向量的负无穷范数：向量的所有元素的绝对值中最小的：上述向量 $\vec{a}$ 的负无穷范数结果就是：5
$\Vert\vec{x}\Vert_{-\infty}=\min{|{x_i}|}$
向量的正无穷范数：向量的所有元素的绝对值中最大的：上述向量 $\vec{a}$ 的正无穷范数结果就是：10
$\Vert\vec{x}\Vert_{+\infty}=\max{|{x_i}|}$
向量的 p 范数
$L_p=\Vert\vec{x}\Vert_p=\sqrt[p]{\sum_{i=1}^{N}|{x_i}|^p}$

矩阵的范数归纳？

定义一个矩阵 $A=[-1, 2, -3; 4, -6, 6]$ 。任意矩阵定义为： $A_{m\times n}$ ，其元素为 $a_{ij}$ ，矩阵的范数定义为
$\Vert{A}\Vert_p :=\sup_{x\neq 0}\frac{\Vert{Ax}\Vert_p}{\Vert{x}\Vert_p}$
矩阵的 1 范数（列范数）：矩阵的每一列上的元素绝对值先求和，再从中取个最大的，（列和最大），上述矩阵 $A$ 的 1 范数先得到 $[5,8,9]$ ，再取最大的最终结果就是：9
$\Vert A\Vert_1=\max_{1\le j\le n}\sum_{i=1}^m|{a_{ij}}|$
矩阵的 2 范数：矩阵 $A^TA$ 的最大特征值开平方根，上述矩阵 $A$ 的 2 范数得到的最终结果是：10.0623 ，其中， $\lambda_{max}(A^T A)$ 为 $A^T A$ 的特征值绝对值的最大值
$\Vert A\Vert_2=\sqrt{\lambda_{max}(A^T A)}$
矩阵的无穷范数（行范数）：矩阵的每一行上的元素绝对值先求和，再从中取个最大的，（行和最大），上述矩阵 $A$ 的行范数先得到 $[6；16]$ ，再取最大的最终结果就是：16
$\Vert A\Vert_{\infty}=\max_{1\le i \le m}\sum_{j=1}^n |{a_{ij}}|$
矩阵的核范数：矩阵的奇异值（将矩阵 svd 分解）之和，这个范数可以用来低秩表示（因为最小化核范数，相当于最小化矩阵的秩 —— 低秩），上述矩阵 A 最终结果就是：10.9287
矩阵的 L0 范数：矩阵的非 0 元素的个数，通常用它来表示稀疏，L0 范数越小 0 元素越多，也就越稀疏，上述矩阵 $A$ 最终结果就是：6
矩阵的 L1 范数：矩阵中的每个元素绝对值之和，它是 L0 范数的最优凸近似，因此它也可以表示稀疏，上述矩阵 $A$ 最终结果就是：22
矩阵的 F 范数：矩阵的各个元素平方之和再开平方根，它通常也叫做矩阵的 L2 范数，它的优点在于它是一个凸函数，可以求导求解，易于计算，上述矩阵 A 最终结果就是：10.0995
$\Vert A\Vert_F=\sqrt{(\sum_{i=1}^m\sum_{j=1}^n{| a_{ij}|}^2)}$
矩阵的 L21 范数：矩阵先以每一列为单位，求每一列的 F 范数（也可认为是向量的 2 范数），然后再将得到的结果求 L1 范数（也可认为是向量的 1 范数），很容易看出它是介于 L1 和 L2 之间的一种范数，上述矩阵 $A$ 最终结果就是：17.1559
矩阵的 p 范数
$\Vert A\Vert_p=\sqrt[p]{(\sum_{i=1}^m\sum_{j=1}^n{| a_{ij}|}^p)}$

如何判定矩阵为正定的？

顺序主子式全大于 0
存在可逆矩阵 $C$ 使 $C^TC$ 等于该矩阵
正惯性指数等于 $n$
合同于单位矩阵 $E$ （即：规范形为 $E$ ）
标准形中主对角元素全为正
特征值全为正
是某基的度量矩阵

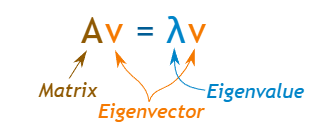
什么是矩阵的特征值 (eigenvalue)、特征向量 (eigenvectors)?

对于方阵 A，特征向量 $v$ 和特征值 $\lambda$ 使此方程成立
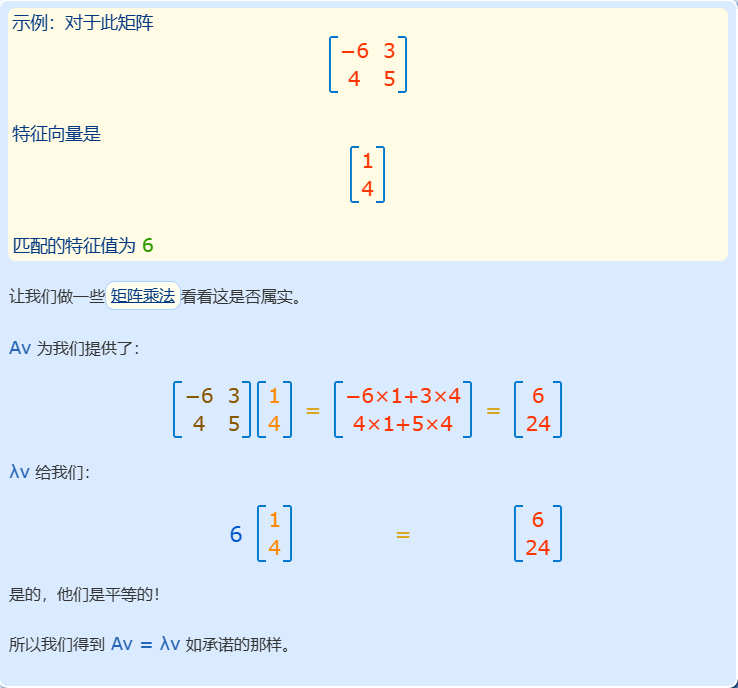
举例：以上公式矩阵乘以向量，并得到与将标量（只是一个数字）乘以该向量时相同的结果

如何求特征值与特征向量？

(1) 从找到特征值开始，已知以下等式一定是正确

A\nu = \lambda \nu

(2) 加入一个恒等矩阵

A\nu = \lambda I \nu

(3) 如果 $v$ 不为 0，去掉后得到以下式子，在此基础上求解特征值

\mid A\nu - \lambda \nu \mid=0

(4) 得到特征值后，带入式子 (1) 求解特征向量

奇异值与特征值有什么关系？

将一个矩阵 $A$ 的转置乘以 $A$ ，并对 $A^TA$ 求特征值，则有下面的形式
$(A^TA)V = \lambda V$
这里 $V$ 就是上面的右奇异向量，另外还有
$\sigma_i = \sqrt{\lambda_i}, u_i=\frac{1}{\sigma_i}AV$
这里的 $\sigma$ 就是奇异值， $u$ 就是上面说的左奇异向量，奇异值 $\sigma$ 跟特征值类似，在矩阵 $\sum$ 中也是从大到小排列，而且 $\sigma$ 的减少特别的快，在很多情况下，前 10% 甚至 1% 的奇异值的和就占了全部的奇异值之和的 99% 以上了，也就是说，我们也可以用前 $r$ ( $r$ 远小于 $m,n$ ）个的奇异值来近似描述矩阵，即部分奇异值分解：
$A_{m\times n}\approx U_{m \times r}\sum_{r\times r}V_{r \times n}^T$
右边的三个矩阵相乘的结果将会是一个接近于 $A$ 的矩阵，在这儿， $r$ 越接近于 $n$ ，则相乘的结果越接近于 $A$