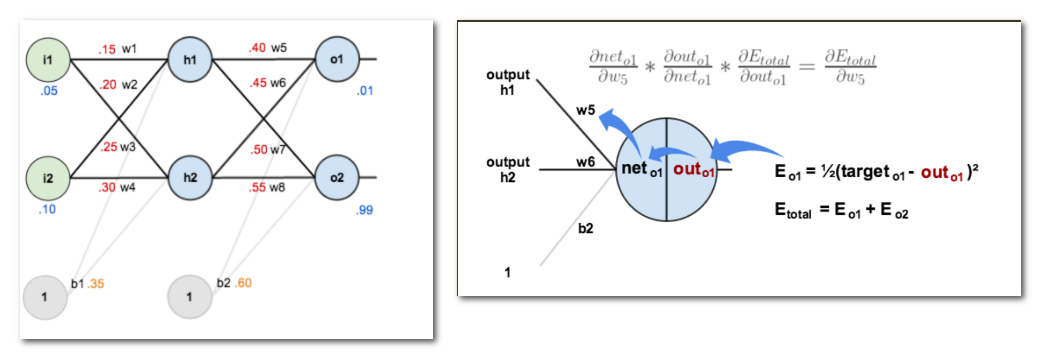
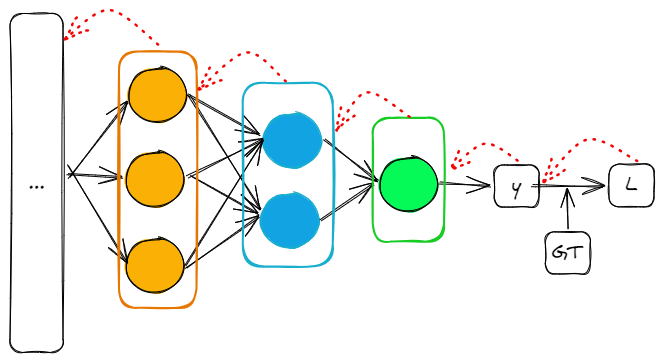
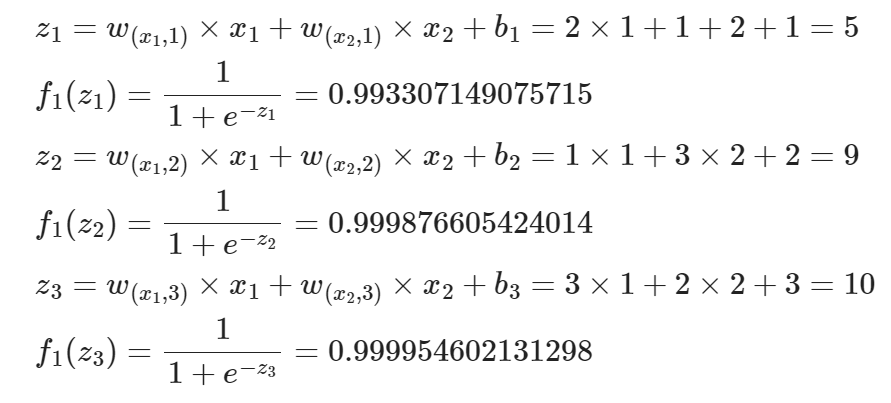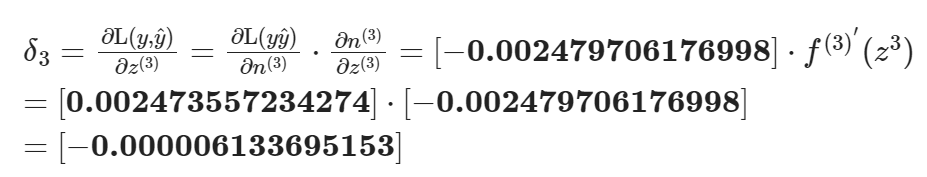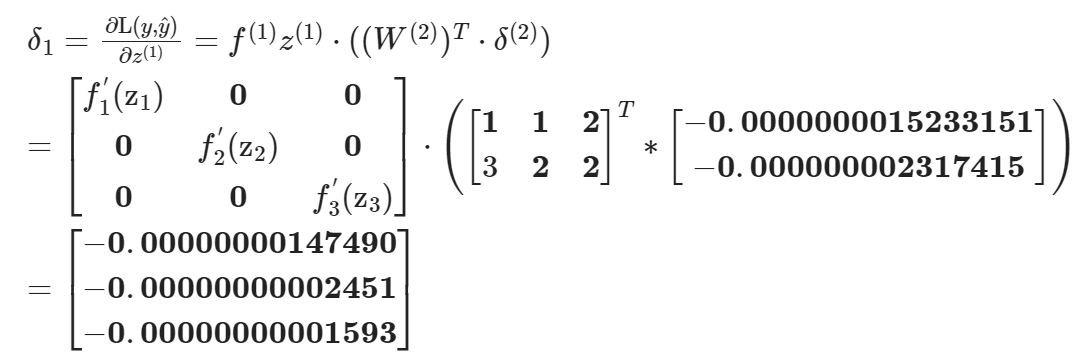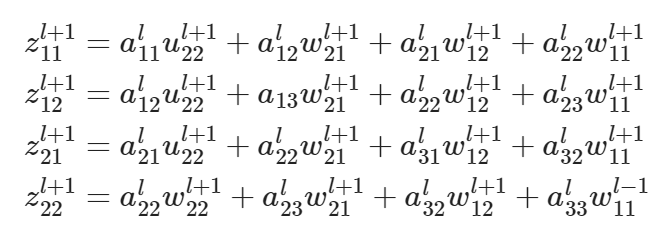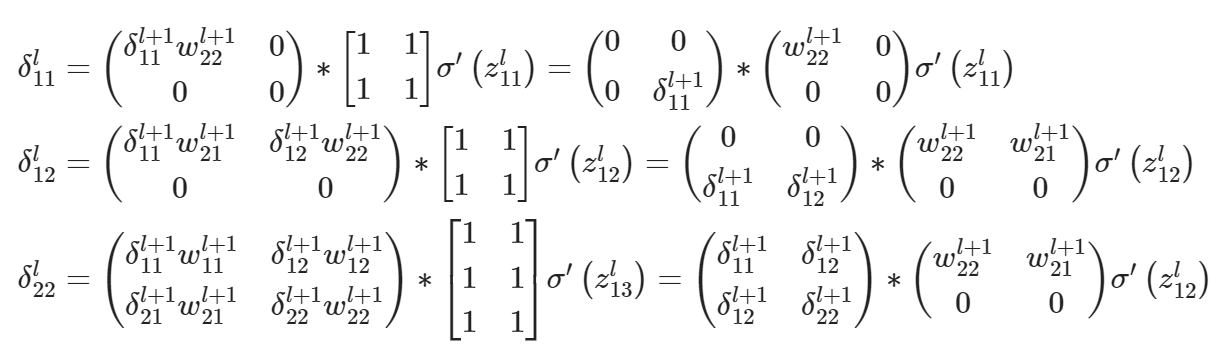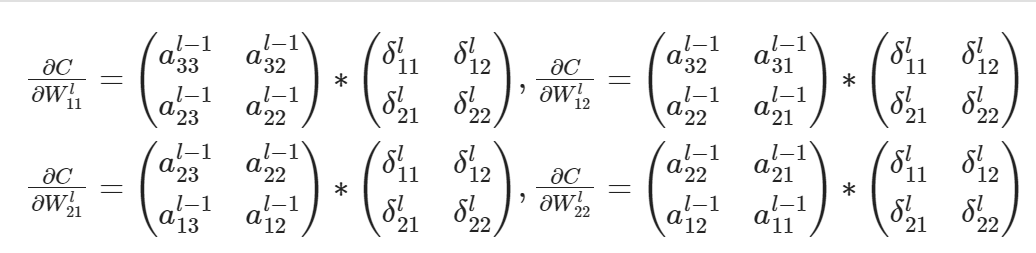本文介绍 BP 算法的原理,尤其需要把握的时,损失先对每层输出求误差项,然后将误差项应用于每一层参数,求得所有参数的梯度,然后再使用优化器去更新参数
什么是反向传播算法 (Backpropagation, BP)?
![]()
- 深度学习的基石算法,它通过模型的损失,反向求取模型 “可学习参数的更新梯度”,以便后续通过优化器更新模型参数
- 反向传播算法由两个过程组成:1)前向计算:将数据输入送入网络以获得预测结果,对预测结果同训练目标求差得到损失;2)反向传播:根据损失更新网络权重
- 实际上,如果要继续细分,更新权重不是 BP 算法做的,而是优化器做的,BP 只是将损失对权重的梯度返回到每一层网络
反向传播算法计算梯度的原理?
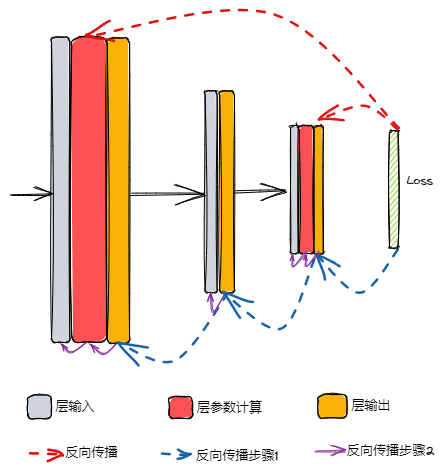
![Drawing 2023-05-01 17.30.32.excalidraw|369]()
- 求取参数梯度的过程,就是模型输出损失 + 链式法则 求偏导数的过程,具体步骤分为 2 个步骤:(1) 根据损失求得损失关于每层网络输出(激活前)的梯度;(2) 在每层网络上求取梯度,如果没有可学习参数,则直接输出关于输入的梯度,然后往前面传递,如池化层、dropout 层;如果该层网络有参数,先计算输出关于参数的梯度,然后计算输出关于输入的参数,如线性层、卷积层等
- 上图是 3 层神经网络的反向梯度传播过程,每一层包含输入、参数计算、输出 3 个过程,其中中间一层没有参数,理想情况下是求得 Loss 关于所有参数的梯度 (红线),实际计算需要按照链式法则求得 Loss 关于每一层输出的梯度(蓝线),然后在每一层内计算损失关于参数的梯度 (紫线)
训练神经网络时的损失、反向传播、优化器的区别与联系?
![Drawing-2023-04-29-11.46.08.excalidraw]()
- 损失:网络前向计算,得到输出后,与 gt 计算损失
- 反向传播:根据损失反向求得损失对每个权重的梯度
- 优化器:根据优化规则,使用梯度更新权重
神经网络中 “误差项” 的理解?
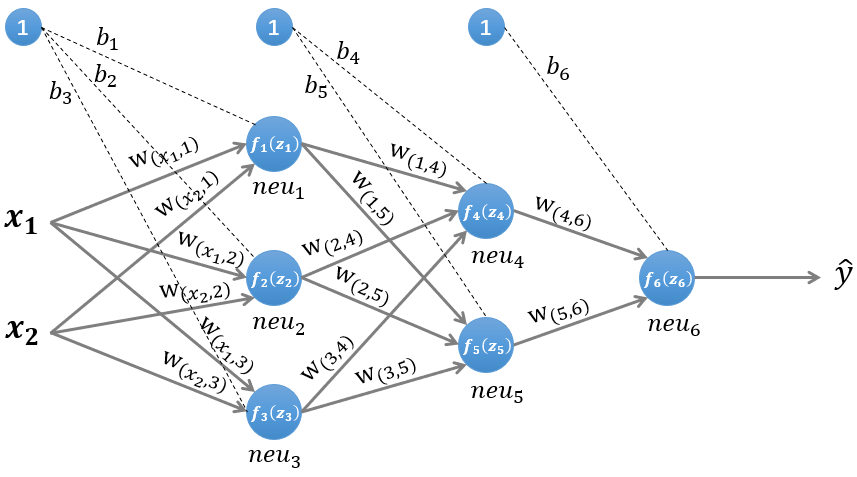
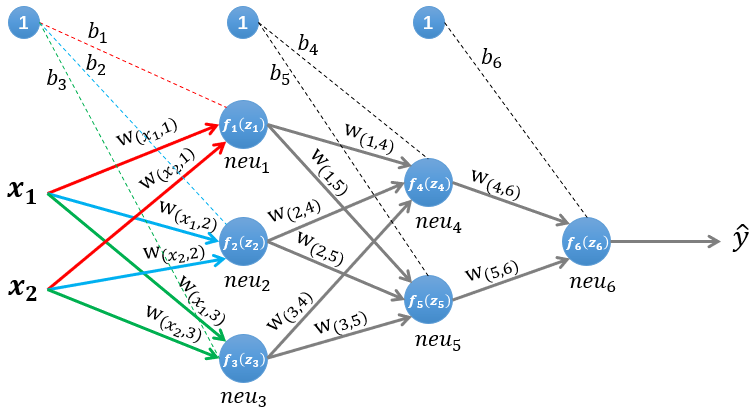
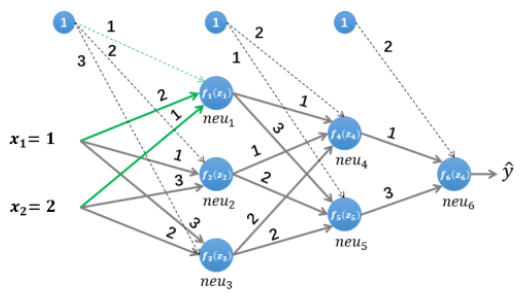
MLP 网络的前向推理?
![]()
- 本例是一个三层的 MLP 网络 (2 层隐藏层,1 层输出层),前向计算时每层内的所有神经元都感知所有输入(乘积和),以下计算不考虑激活函数
- 第一层隐藏层输出:
![]()
z1=w(x1,1)∗x1+w(x2,1)∗x2+b1z2=w(x1,2)∗x1+w(x2,2)∗x2+b2z3=w(x1,3)∗x1+w(x2,3)∗x2+b3
- 第二层隐藏层输出:
![]()
z4=w(1,4)∗z1+w(2,4)∗z2+w(3,4)∗z3+b4z5=w(1,5)∗z1+w(2,5)∗z2+w(3,5)∗z3+b5
- 输出层计算:
![]()
z6=w(4,6)∗z4+w(5,6)∗z5+b6
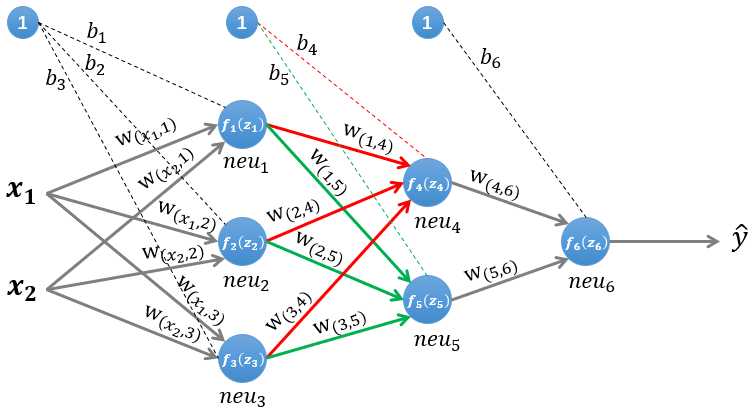
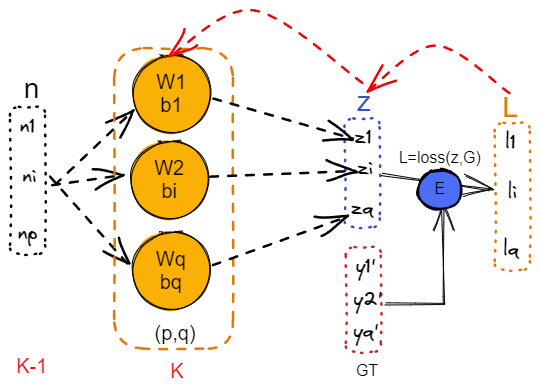
MLP 网络使用 BP 算法进行后向传播?
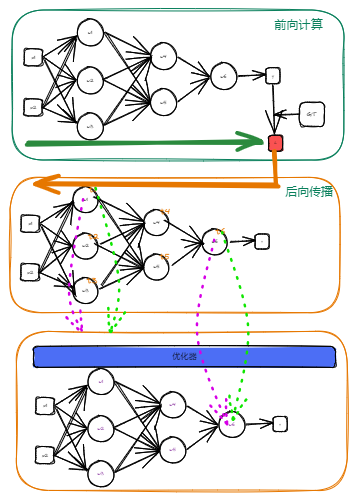
![Drawing-2023-04-29-13.37.23.excalidraw]()
- 以 MLP 为例,上图是对 K-1 层的 p 个输出,使用第 K 层中 q 个感知机进行前向推理的过程(未考虑激活函数),其中红色线表示 BP 算法依次反向求输出或者参数的梯度
- 前向推理:n->z->L 的过程,即计算神经元输出的过程、损失的过程
z(k)=W(k)×n(k−1)+b(k)L=L(y,y^)
- 后向传播:根据链式求导法则,有
∂W(k)∂L(y,y^)=∂z(k)∂L(y,y^)∗∂W(k)∂z(k)∂b(k)∂L(y,y^)=∂z(k)∂L(y,y^)∗∂b(k)∂z(k)(1)
- 求偏导数 ∂W(k)∂z(k):根据公式 z(k)=W(k)×n(k−1)+b(k) 结合每个神经元都单独感知全部输入,可知
∂W(k)∂z(k)=⎣⎢⎢⎢⎢⎢⎢⎡∂W(k)∂(W1(k)+n(k−1)+b(k))⋮∂W(k)∂(Wm(k)+n(k−1)+b(k))⎦⎥⎥⎥⎥⎥⎥⎤⟹(n(k−1))T(2)
- 求偏导数 ∂b(k)∂z(k):b 是一个常数项,其偏导数为单位矩阵,大小为该层的神经元格式,这里是 q,所以是 qxq 大小的单位矩阵
∂b(k)∂Z(k)=⎣⎢⎢⎢⎡∂b1∂(W1(k)+n(k−1)+b1)⋮∂b1∂(Wm(k)+n(k−1)+bm)………∂bm∂(W1(k)+n(k−1)+b1)⋮∂bm∂(Wm(k)+n(k−1)+bm)⎦⎥⎥⎥⎤=⎣⎢⎢⎡1⋮0………0⋮1⎦⎥⎥⎤(3)
- 求偏导数 δ(k)=∂z(k)∂L(yy^):表示该层权值输出关于损失的偏导数,称为误差项,可理解为该层输出对误差的贡献,已知 z(k+1)=W(k+1)∗n(k)+bk+1,n(k)=fk(z(k)),根据链式法则得到
δ(k)=∂z(k)∂L(y,y^)=∂z(k)∂n(k)⋅∂n(k)∂z(k+1)⋅∂z(k+1)∂L(y,y^)=∂z(k)∂n(k)⋅∂n(k)∂z(k+1)⋅δ(k+1)=fk′(z(k))⋅((W(k+1))T⋅δ(k+1))(4)
- 汇总结果:汇总将公式 2,3,4 到 1 得到
∂W(k)∂L(yy^)=∂z(k)∂L(yy^)∗∂W(k)∂z(k)=δ(k)∗(n(k−1))T∂b(k)∂L(yy^)=∂z(k)∂L(yy^)∗∂b(k)∂z(k)=δ(k)(5)
- 根据以上公式,可知:1) 神经网络对权重的偏导数,等于当前层关于损失的偏导数乘上输入的转置;2)只要求得每层输出关于权重的误差项,那么权重的更新梯度就很容易求得,根据公式 4 可知,第 k 层的误差项可以通过 k+1 层的误差项求得,而最后一层的误差项是损失函数,所以递归求回去就得到每一层的误差项
MLP 网络中,BP 算法和优化器更新网络参数的流程?
![Drawing-2023-04-29-15.47.27.excalidraw]()
- (1) 前向计算得到损失:前向计算得到网络输出,然后计算损失,需要输入、网络、GT
z(k)=W(k)×n(k−1)+b(k)L=L(y,y^)
- (2) 通过公式 4 计算每层网络的误差项:通过输出层的损失,结合每层网络的权重和输出,计算得到所有层的偏差项,可理解为该层输出对误差的贡献,需要 Loss (即最后一层误差项)、k+1 层的误差项、k 到 k+1 层的权重 (转置)、k 层激活函数对该层输出的梯度
δ(k)==fk′(z(k))⋅((W(k+1))T⋅δ(k+1))
- (3) 通过公式 5 计算每层网络参数的梯度: 得到偏差项后,通过公式 5 计算所有权重的梯度,每个参数都有一个梯度
- Pythorch 为每个需要训练的参数记录梯度,通过
requires_grad=True 控制,训练时先使用 optim.zero_grad() 清空所有参数的梯度,然后通过 loss.backward() 计算所有参数的梯度,最后使用 optim.step() 根据梯度及优化器更新网络参数∂W(k)∂L(yy^)=∂z(k)∂L(yy^)∗∂W(k)∂z(k)=δ(k)∗(n(k−1))T∂b(k)∂L(yy^)=∂z(k)∂L(yy^)∗∂b(k)∂z(k)=δ(k)
- (4) 更新网络参数: 通过优化器规则更新参数,需要 K 层的梯度、学习率、K 层的权重
W(k)=W(k)−α(δ(k)(n(k−1))T+W(k))b(k)=b(k)−αδ(k)
例子:MLP 前向计算过程?
![]()
- 假设所以层均使用激活函数 f<!−−swig0−−>(z)=1+e−z1
- 第一层隐藏层输出:
![深度学习之反向传播BP算法详解-20250116162231]()
- 第二层隐藏层输出:
![深度学习之反向传播BP算法详解-20250116162218]()
- 输出层:
![深度学习之反向传播BP算法详解-20250116162159]()
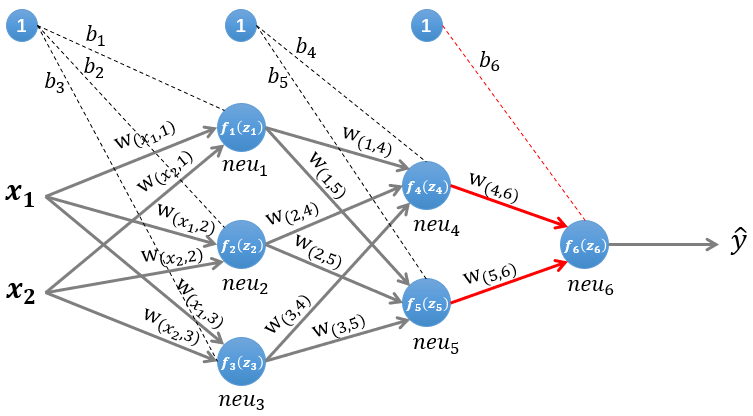
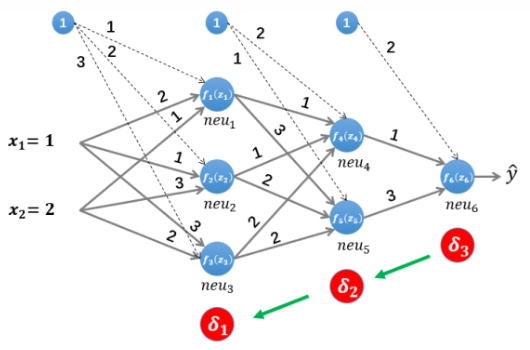
例子:MLP 后向传播过程?
CNN 网络的后向传递过程?
参考:
- 一文彻底搞懂 BP 算法:原理推导 + 数据演示 + 项目实战(下篇) - 知乎
- 神经网络学习(十二)卷积神经网络与 BP 算法_bp 神经网络和卷积神经网络区别_oio328Loio 的博客 - CSDN 博客
- 卷积神经网络 (CNN) 反向传播算法 - 刘建平 Pinard - 博客园
- 如何解读 CNN 的反向传播计算算法? - 知乎
![]()
![Drawing 2023-05-01 17.30.32.excalidraw|369]()
![Drawing-2023-04-29-11.46.08.excalidraw]()
![]()
![]()
![]()
![]()
![Drawing-2023-04-29-13.37.23.excalidraw]()
![Drawing-2023-04-29-15.47.27.excalidraw]()
![]()
![深度学习之反向传播BP算法详解-20250116162231]()
![深度学习之反向传播BP算法详解-20250116162218]()
![深度学习之反向传播BP算法详解-20250116162159]()
![]()
![深度学习之反向传播BP算法详解-20250116162141]()
![深度学习之反向传播BP算法详解-20250116162124]()
![深度学习之反向传播BP算法详解-20250116162101]()
![深度学习之反向传播BP算法详解-20250116162021]()
![深度学习之反向传播BP算法详解-20250116161953]()
![深度学习之反向传播BP算法详解-20250116161930]()
![深度学习之反向传播BP算法详解-20250116161908]()
![深度学习之反向传播BP算法详解-20250116161835]()