KD

发表于 2023-03-13 更新于 2025-01-18 分类于 2-深度学习， D-深度学习部署，模型蒸馏阅读次数：本文字数： 2.2k 阅读时长 ≈ 2 分钟

知识蒸馏的开山之作，通过使用带温度的 softmax 函数来软化 teacher 网络的逻辑层输出作为 student 网络的监督信息，以达到使用小模型学到大模型知识的目的

什么是 Distilling the Knowledge in a Neural Network ？

知识蒸馏的开山之作。在实际情况中，复杂的模型往往能学习到更多的数据变化，其效果会更好，但是复杂的模型往往不利于部署落地，有没有一种办法将大模型学习到的知识 / 经验过渡到小模型呢？答案是蒸馏
论文以 “teacher-student” 的方式搭建模型，其中 teacher 是复杂模型或者多个组合模型，蒸馏的目的是将 teacher 的泛化能力迁移到 student

为什么模型可以被 “蒸馏”？

对于 “teacher-student” 方式的蒸馏模型，teacher 模型够学习区分大量的类别，正常情况下，训练目标是最大化正确类别的平均对数概率，但这种学习的副作用是训练的模型会将概率分配给错误的类别上，虽然这些概率值可能很小，但一些错误类别比其他错误类别的概率值大很多，如将轿车误认为是垃圾车的概率明显比误认为萝卜的概率大。在错误类别上的相对概率可以反映出模型是如何进行泛化的
如果 student 模型能学习到 teacher 在所有图片、所有类别上的泛化能力，就意味着 student 模型具备 teacher 模型的能力。实际操作时，如果让 student 单纯学习 gt 标签，相当于模型从 0 开始学习，所以 student 模型同时学习 teacher 输出和 gt 标签

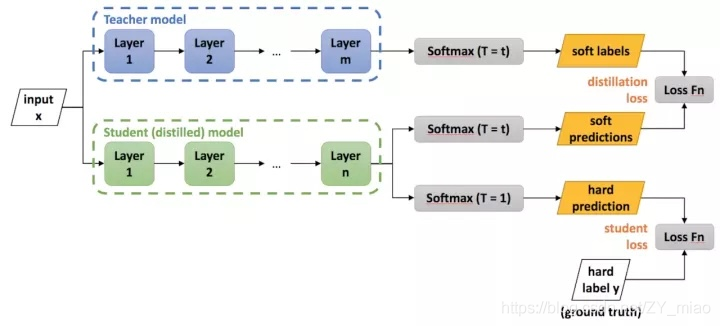
Distilling the Knowledge in a Neural Network 的网络结构？

软目标 (soft label)：teacher 模型的输出，经过变换的值。对于这个迁移阶段，可以使用相同的训练集或单独的 “迁移” 集。当 teacher 模型是小模型的集成时，我们使用小模型各自预测的概率分布的算术或几何平均作为 “软目标”。
硬目标（hard label）：图片的真实标签
蒸馏时，使用软目标和硬目标联合训练 student 模型。当软目标具有高熵值，在训练每一个样本时软目标能够提供比硬目标（student) 模型的 (ground truth）更多的信息并且训练每一个样本时的梯度差异更小。因此，与 teacher 模型相比，student 模型训练数据要少得多，使用的学习率也高得多

为什么 teacher 的输出需要使用 “温度 T” 变换？

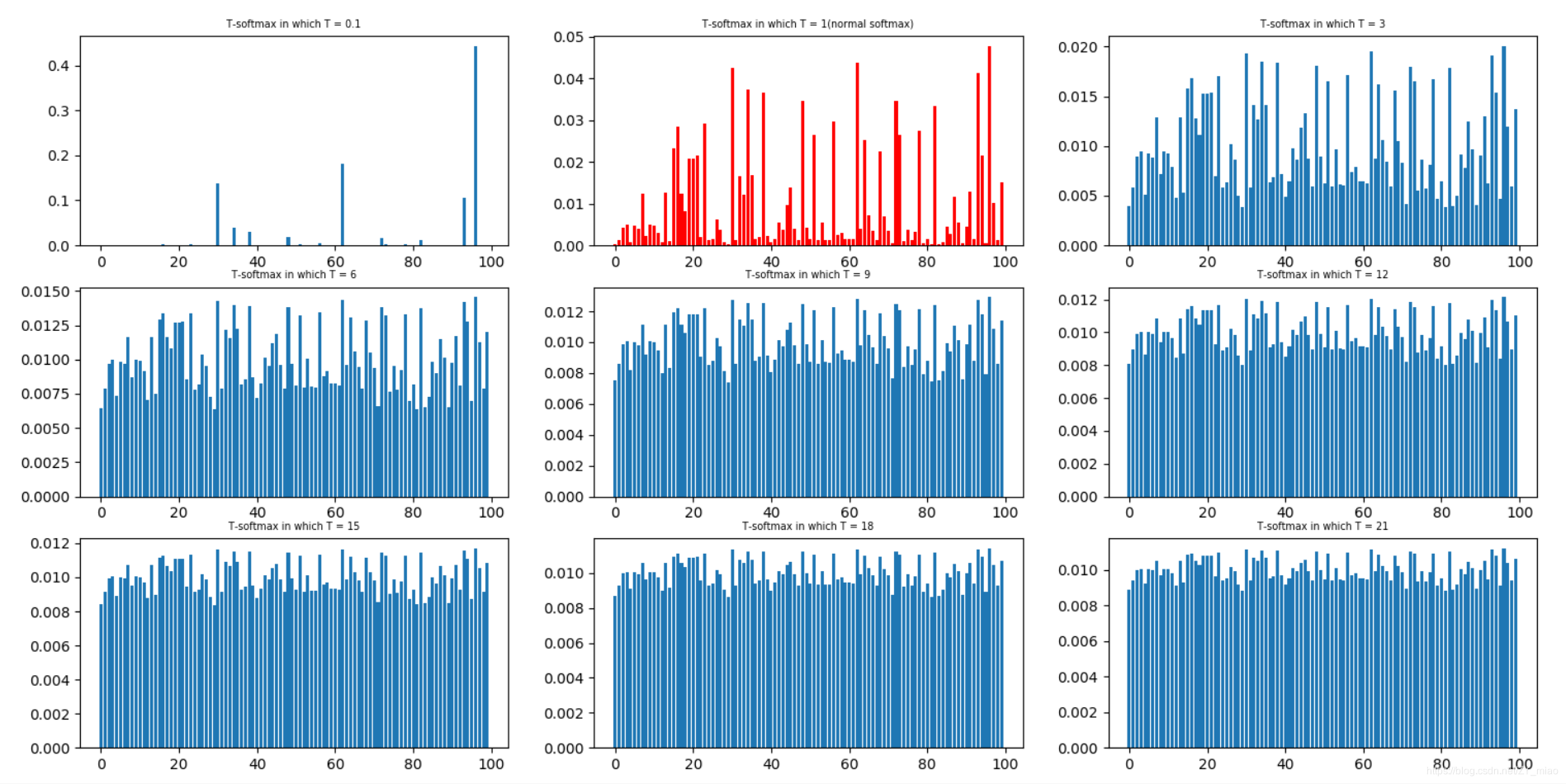
对于像 mnist 一样的任务，teacher 模型通常能够在正确类别上有高置信度，在错误类别上有很小概率，但是有差别，比如 “2” 被误认为 “3” 的概率是 10 e-6，被误认为 “7” 的概率是 10 e-9，其他 “2” 的图片又可能有相反表现。这种泛化差异对 student 模型的学习很有用，但是交差熵后的值却很小，无法作为差异信息被学习
论文先将 teacher 模型的输出 z 除于温度 T，再变换后的值求 softmax，不同的 T 可以产生不同强度的差异，如图红色是 T=9 的时候各个类别的概

\mathrm{q_i}=\frac{\exp\left(\mathrm{z_i/T}\right)}{\sum_j\exp\left(\mathrm{z_j/T}\right)}

由于软目标计算梯度时有

1/T^2

的缩小，所以更新网络梯度时，软目标的梯度乘上

T^2

。同时即使温度 T 发生变化，也确保软目标和硬目标的共享大致保持不变

class DistillKL(nn.Module):
	"""Distilling the Knowledge in a Neural Network"""
	def __init__(self, T):
		super(DistillKL, self).__init__()
		self.T = T
	def forward(self, y_s, y_t):
		p_s = F.log_softmax(y_s/self.T, dim=1)
		p_t = F.softmax(y_t/self.T, dim=1)
		# 乘上T^2
		loss = F.kl_div(p_s, p_t, size_average=False) * (self.T**2) / y_s.shape[0]
		return loss

Distilling the Knowledge in a Neural Network 的损失函数？

student 模型的损失包含 2 部分，即输出与 teacher 模型输出的交叉熵、输出与 gt 标签的交叉熵，其中输出与 teacher 模型输出的交叉熵经过很大的 “温度 T” 处理，输出与 gt 标签的交叉熵的 “温度 T=1” $$\operatorname {cost function}=\operatorname {CroEntropy}(\mathbf {y_s},\mathbf {y_t})+\mathbf {aCrossEntropy}(\mathbf {y_s},\mathbf {y})$$
由于软目标计算梯度时有 $1/T^2$ 的缩小，所以更新网络梯度时，软目标的梯度乘上 $T^2$ 。同时即使温度 T 发生变化，也确保软目标和硬目标的共享大致保持不变

参考：