深度学习的数学基础

学习深度学习，第一个门槛总是“数学要学什么，学多少？”，本文介绍了需要学习的数学知识

深度学习的基本理论，可以描述为以下过程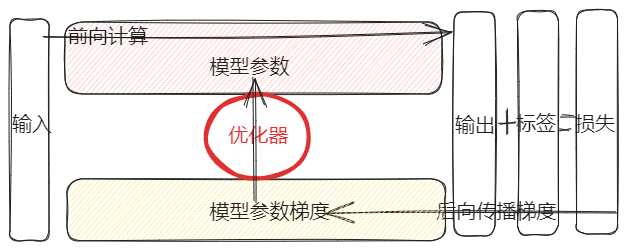

1. 前向计算（输入->输出）：输入数据经过模型参数的计算后得到模型输出
2. 损失计算 (输出+标签=损失)：根据模型输出和真实的标签，计算它们的差距，得到损失
3. 梯度反向传播 (输出+损失->参数梯度)：根据模型输出和损失，计算所有模型参数的梯度
4. 更新参数 (参数+梯度->更新后参数)：优化器根据参数及参数对应的梯度，更新参数

针对这些过程，需要以下数学知识：

数学领域	掌握知识点	对应深度学习步骤
线性代数	掌握矩阵、张量的运算	深度学习的前向计算都是矩阵 (张量)的计算
概率论	掌握概率基础，贝叶斯理论	深度学习其实是一个概率模型，深度学习的目的就是拟合目标概率分布
信息论	掌握熵、条件熵、交叉熵、KL 散度	深度学习的损失计算很多情况下是计算输出概率和真实值的交叉熵
微积分	掌握极限、导数、偏导数	深度学习的后向传播的梯度计算使用了偏导数的概念
最优化理论	掌握梯度下降方法、牛顿发等优化方法	深度学习的后向传播是更新参数的过程，更新的规则就是优化方法

• 线性代数：从标量、向量入手，讲解到矩阵、张量，并讲解了矩阵与张量的运算规则，对于神经网络来说，张量之间更多的是：矩阵相乘(卷积提取特征)、矩阵内积(transformer计算自注意力)
• 概率论：分为两部分，第一部分先从随机变量讲起，然后讲解概率分布、概率质量、概率密度函数，尤其需要把握的是先验概率、后验概率、条件概率、全概率以及贝叶斯定理。第二部分讲解随机变量距离的计算方式
• 信息论：讲解了熵的计算过程，并且延伸到交叉熵、KL散度，这些概念对应神经网络中损失的计算，学习时需要记住熵、交差熵、KL散度即可
• 微积分：本文从极限入手，一步步讲解到导数、偏导数、梯度，是神经网络反向传播的核心，后续在此基础上进一步展开讲解到泰勒公式，泰勒公式其实就是使用多阶导数去接近原始函数，就是韩式表达式的分解表示，类似与神经网络向不同层进行后向传播
• 最优化理论：本文讲解了常用的优化算法，对应深度学习的优化函数，实际学习可以是最小二乘法->座标下降->梯度下降->牛顿