深度图展平方法研究

将 0-65535 数值范围的深度图，通过 “展平” 的方式，处理为 0-255，降低数值范围的同时凸现目标缺陷。展平的核心思路是构建目标平台的 “标准 3D 图”，通过 “实际 3D 图 - 标准 3D 图” 得到凸现缺陷的 “差图”，然后将差图拉升到 0-255，实现展平

利用标准深度图求差分图

该方法能求差分图的前提是两张图片对齐，如果不对齐，求出的差分图无法凸现缺陷。所以第一步尝试将标准深度图与任意缺陷图片对齐，对齐思路是：

由于图片是 2D+3D 一组图片，所以使用以下方法在 2D 图片对齐，然后在 3D 图片求差分图

1. 使用 2D 特征查找算子 SIFT 找到两张图片关键点
2. 使用 BFMatcher 匹配关键点
3. 过滤选择评分高的匹配点，选择其中 3 个点计算两张图转换的放射变换矩阵
4. 利用放射变换矩阵变换对应 3D 图
5. 求差分图

以下是通过 1-3 过程，选取前 100 配对的匹配点，可以看出大部分匹配点连线是平行的，说明另一个图可以通过平移实现 和另一个图对齐，但是如果选择的是不平行匹配点对，就无法实现对齐

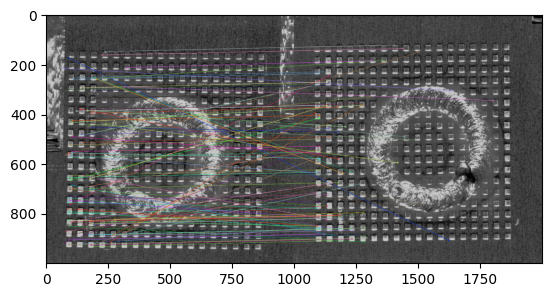
总的来说，以上方法做全图的对齐很难，并且标准图不适合用于位置变动的图像上，即使实现了全图对齐，缺陷所在的圈不对齐，求得的差分图也无法突出这个圈上缺陷。

如果先分割出圈，然后对齐在求差分图呢？这样局限性也很多，数据变少，对齐不好做，如果圈大小不同，问题就更多，因此这个方法局限很大

基于线拟合求标准平面

假设面对的 3D 图片有一个基座平台，通过抽取垂直或者横向的每一条数据线，然后使用一次或者 2 次函数拟合，所有的拟合线组成拟合面，也就是标准平面

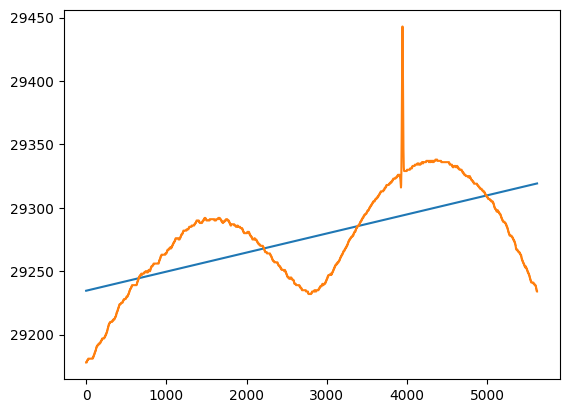
如上图所示，假设曲线是 3D 图某个方向的一条曲线，通过一次函数拟合后得到蓝线，在所有位置求篮线得到标准平面，原始图片减去标准平面得到差分平面，通过这个方法得到以下差分平面

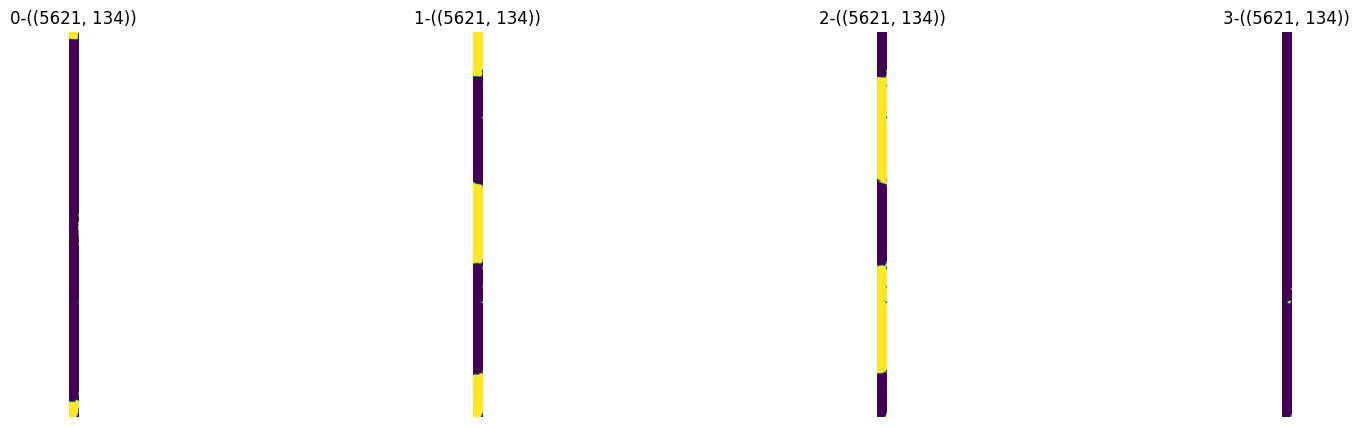
由图可知，在平台不是 “方向刚性” 的情况下，另一个方向的起伏就导致该方法失败，假设使用二次拟合呢？比如下图通过橙色线拟合蓝线

![[Pasted image 20250201100328.png]]

也过还是和一次拟合类似，无法避免

通过平面拟合求标准图片

线拟合知识考虑一个方向，存在缺陷性，本方法通过在局部考虑多个方向实现求标准图，比如通过选择少数的点，做曲面拟合，曲面拟合的面就是标准图片，下图分别是采样点、拟合面、采样点 + 拟合面

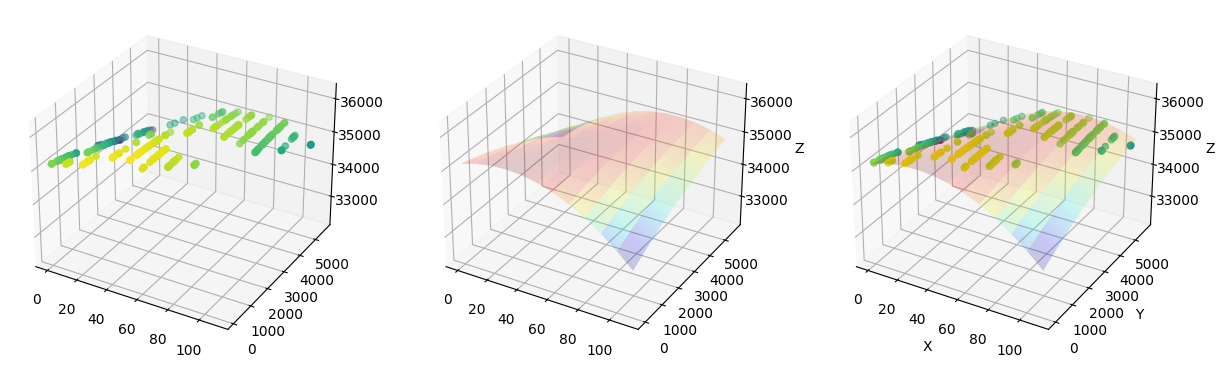
这个方法依赖于采样点，并且如果出现落差很大的区域时，会影响周围区域，无法平稳过渡，下图分别是图片、原始深度、拟合平面、差分图及差分图二值化，可以看出二值化后没有凸现缺陷

通过滤波求标准图片

除通过曲面拟合考虑多个方向的起伏外，还可以通过大卷积核的高斯滤波过滤图片，并将其作为原图的拟合平面，原图 - 拟合平面 = 差分图

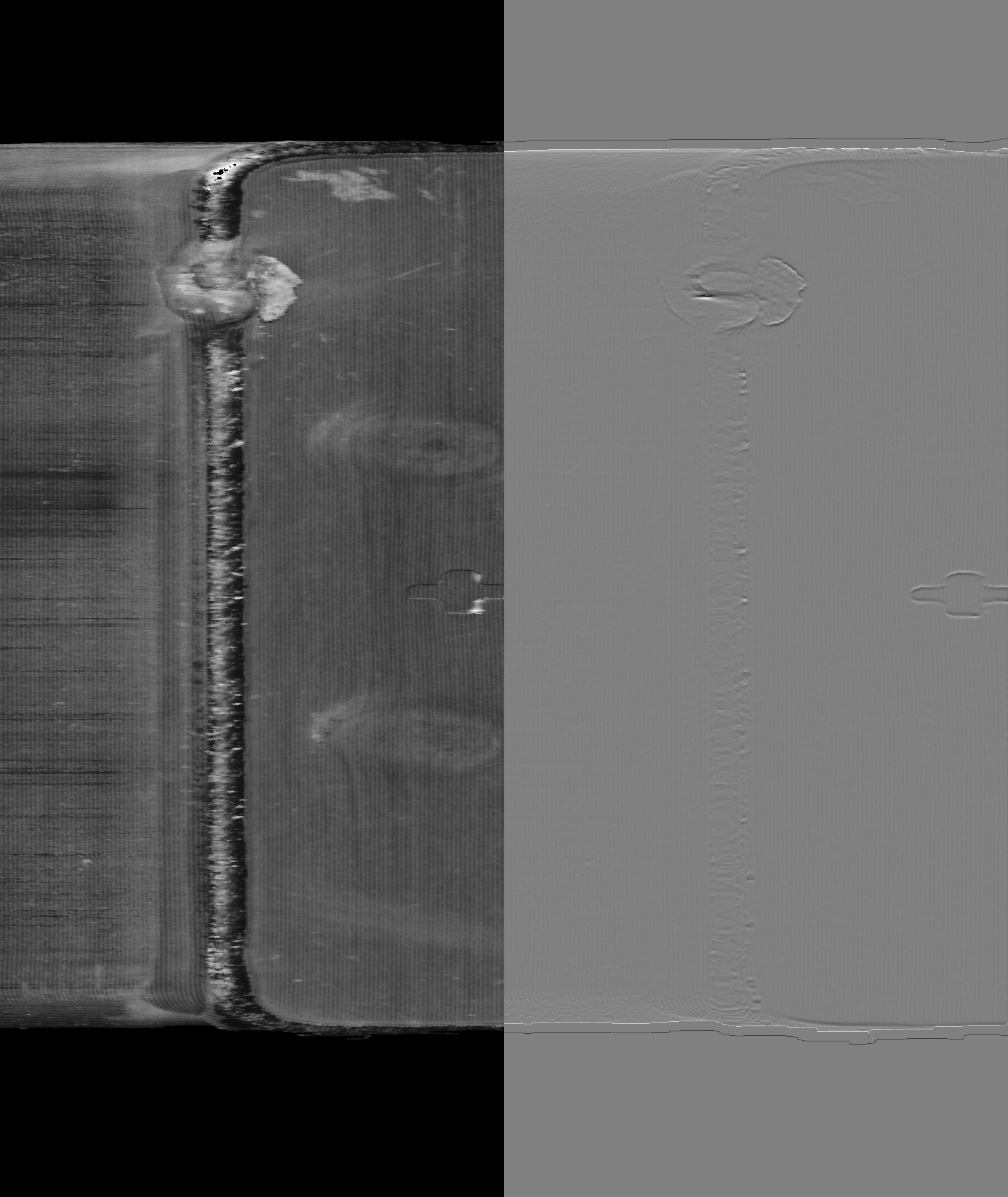
看得出来，比之前效果好多了

通过局部直方图均衡化求标准图

进一步的，高斯核需要针对不同图片手动调整，稳定性较差，我们通过局部直方图均衡化替代这个过程

def gen_flattening_image(tif,grid_w=30,grid_h=30,threshold=40):
    # 局部均衡化
    clahe = cv2.createCLAHE(clipLimit=threshold, tileGridSize=(grid_w, grid_h))
    cl1 = clahe.apply(tif)
    # fp32->uint8
    cl1=cl1.astype(np.float32)
    
    # 对比度拉伸
    cl1-=np.min(cl1)
    cl1/=(np.max(cl1)-np.min(cl1))
    cl1*=255
    res=np.round_(cl1)
    
    return res

下图分别是原图、直接拉伸截图和采样局部直方图均衡化后的结果，可以看出本方法效果更好

将最后一个方法使用 nuitka 打包为工具，可以快速处理批量图片