You Only Look Once：Unified Real-Time Object Detection

发表于 2020-06-02 更新于 2023-10-24 分类于 2-深度学习， D-目标检测阅读次数：本文字数： 7.2k 阅读时长 ≈ 7 分钟

目标检测全新检测方式，相比较过去的二阶段检测方法，YOLO 系列系列将模型输出看作网格，图片的目标落在网格上，输出“网格数量的”预测实现对目标的检测

什么是 YOLOv1?

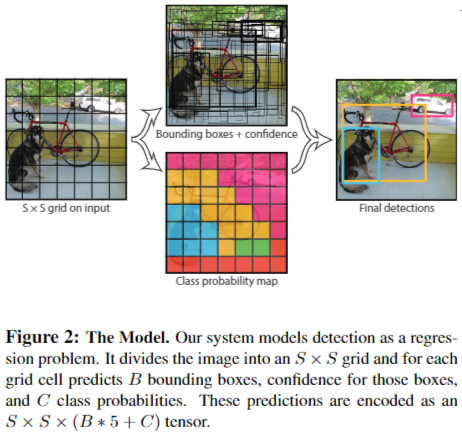
将输入图像分成SxS个格子，每个格子负责检测落入该格子的物体。图中物体马的中心点（红色原点）落入第4行、第3列的格子内，所以这个格子负责预测图像中的物体马

YOLOv1的网络结构？

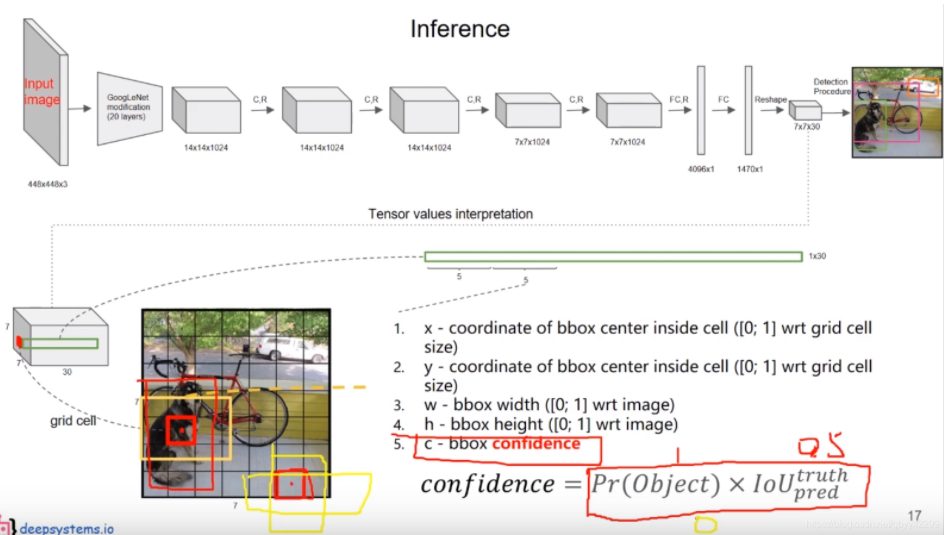
YOLOv1的Backbone借鉴了GoogleNetv1设计，共包含24个卷积层，2个全连接层
输入： 448 x 448 x 3，由于存在全连接层，因此要求输入固定
输出： 最后一个 FC 层得到 1470 x 1 的输出，reshape 一下得到 7 x 7 x 30 的一个 tensor，即最终每个单元格都有一个 30 维的输出，表示每个单元格分为 20 类+2 个预测框，每个预测框包括 4 个位置信息及 1 个置信度。具体如何制作、学习这 30 维变量的学习样本，参考：YOLOv1的正负样本判定、YOLOv1正样本制作过程

YOLOv1如何计算损失？

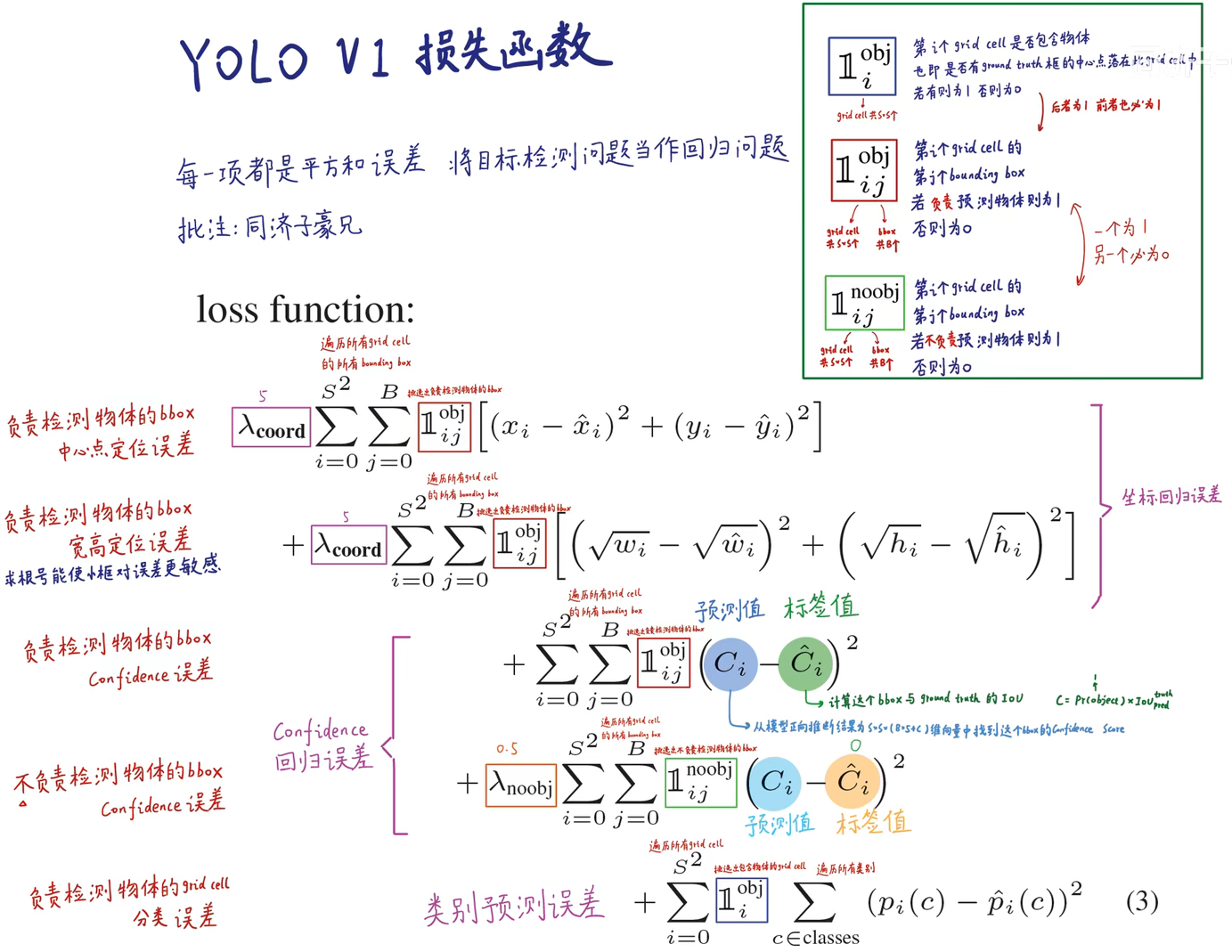
YOLOv1的损失包含3部分，分别是座标回归误差、置信度回归误差、类别误差
注意：只有框真实置信度=1，才表示该框需要被学习位置信息和类别信息；框真实置信度=0（该框无预测目标），只计算框置信度损失
由此可知，有物体的地方，我们让网络去学习，逼近它，而没有物体的地方，理论上应该让 $c_x,c_y,w,h$ 都是零

YOLOv1的正负样本判定？

YOLOv1不存在锚框，因此通过预测框与真实框的IOU判定正负样本，动态变化
位置判定正负样本： 根据真实框对应 cell 位置，将预测框分为正负样本，每个真实框分配 1 个预测框
正样本： 取cell对应的预测框IOU最大的样本为正样本
负样本： cell位置上除正样本外的预测框

YOLOv1正样本制作过程？

YOLOv1 输出是 7x7x30，将图像的真实目标映射到所有网格的 30 维向量即完成样本制作
框置信度： 如果目标的中心落在网格内，则c=1，否则c=0
框的中心： 假设真实座标为 $(x_{min},y_{min},x_{max},y_{max})$
- (1)计算中心 $\begin{array}{l} \text { center } x=\frac{x_{\min }+x_{\max }}{2} \\ \text { center }_{y}=\frac{y_{\min }+y_{\max }}{2} \end{array}$
- (2)计算映射到的网格 $\operatorname{grid}_{x}=\left\lfloor\frac{\text { center }}{\text { stride }}\right\rfloor \operatorname{grid}_{y}=\left\lfloor\frac{\text { center }}{\text { stride }^{y}}\right\rfloor$
- (3) 计算量化误差，量化误差即是网络学习的目标，可知 $0 \leq c_{x}, c_{y} \leq 1$ $\begin{array}{l} c_{x}=\frac{\text { center } r_{x}}{\text { stride }}- \left\lfloor\frac{\text { center } r_{\mathrm{x}}}{\text { stride }}\right\rfloor \\ c_{y}=\frac{\text { center } r_{y}}{\text { stride }}-\left\lfloor\frac{\text { center } r_{\mathrm{y}}}{\text { stride }}\right\rfloor \end{array}$

框的宽高―

(1) 计算框的宽、高 $w=x_{max}-x_{min}， h=y_{max}-x_{min}$
(2)归一化：图像的宽高通常是远大于1的实数，直接用这个做标签，loss 值和其他部分差距很大，因此将其进行归一化处理，最后 $0 \leq w, h \leq 1$ $w=\frac {w} {w_{image}}\\ h=\frac {h} {h_{image}}$
取对数：因为线性回归数是任意实数，而宽高始终大于 0，所以通过对数函数转换其范围 $w=log(w)\\ h=log(h)$

# 第一个目标使用13*13的那个框进行预测，并计算中心偏差、大小及权重
# 以下框的位置及大小的预测：位置使用(7,9)网格进行预测，预测参数为0.6049999999999995 0.4986666666666668 3.9269510260123828 4.9557894982104695
xmin, ymin, xmax, ymax = gt_label[:-1]
print(xmin, ymin, xmax, ymax) # 0.524 0.56 0.646 0.9013333333333333 经过缩放的框x,y,w,h
# 计算边界框的中心点
c_x = (xmax + xmin) / 2 * w
c_y = (ymax + ymin) / 2 * h
box_w = (xmax - xmin) * w
box_h = (ymax - ymin) * h
print(c_x,c_y,box_w,box_h) # 243.35999999999999 303.95733333333334 50.751999999999995 141.99466666666663 原始的框x,y,w,h
# 计算中心点所在的网格坐标
c_x_s = c_x / s
c_y_s = c_y / s
grid_x = int(c_x_s)
grid_y = int(c_y_s)
print(c_x_s,c_y_s,grid_x,grid_y) # 7.6049999999999995 9.498666666666667 7 9 确定模拟待拟合的中心，即原始的框映射到预测位置 
# 计算中心点偏移量和宽高的标签
tx = c_x_s - grid_x
ty = c_y_s - grid_y
tw = np.log(box_w)
th = np.log(box_h)
print(tx,ty,tw,th) # 0.6049999999999995 0.4986666666666668 3.9269510260123828 4.9557894982104695 确定模型待拟合的参数，x,y的偏差,w,h的对数值
# 计算边界框位置参数的损失权重
weight = 2.0 - (box_w / w) * (box_h / h) 
print(weight) # 1.9583573333333333

YOLOv1如何解析模型输出？

总体步骤：使用置信度阈值，过滤低置信度的预测，然后将剩下预测还原到原图上，并使用 nms 第二次过滤
框中心： 利用预测的框的位置 $grid_x,grid_y$ 、下采样倍数 $stride$ 、量化误差 $c_x,c_y$ 得到框的中心

定义回归中心参数为：
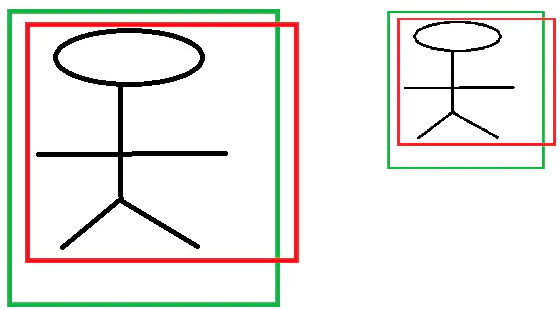
$\Delta x=\left(t^{x}-b^{x}\right) / b^{w}\\ \Delta y=\left(t^{y}-b^{y}\right) / b^{h}$
假设图中是同一目标在不同尺度下的预测效果，已知卷积神经网络具有尺度不变性 (size invariance) ，可以出现左图红框中心到绿框中心为4，红框宽高为(6,6)，右图红框中心到绿框中心为2，红框宽高为(3,3)，不使用除法时，左图平移变换距离为4，右图为2，神经网络输出需要优化>1的数比较困难，因此将待优化值归一化处理(待优化值/先验框中心位置)，则左图和右图优化值均值2/3

YOLOv1边框回归中尺度变换(回归尺寸)，为什么是真实框与先验框比值取log？

定义尺寸变换回归参数为： $\Delta w=\log \left(t^{w} / b^{w}\right)\\ \Delta h=\log \left(t^{h} / b^{h}\right)$
神经网络输出的放缩的尺度 $\Delta w,\Delta h$ 必须大于0。怎么保证满足大于0呢？直观的想法就是 EXP 函数，也即 $\hat g^w=b^w*e^{\Delta w} \\ \hat g^h=b^h*e^{\Delta h}$
尺度变换的目地是为了 $\hat g_w \approx t_w,\hat g_h \approx t_h$ ，所以待学习参数计算公式为： $\Delta w=\log \left(t^{w} / b^{w}\right), \Delta h=\log \left(t^{h} / b^{h}\right)$

YOLOv1预测有多个靠近的格点预测了同一物体，如何处理？

yolov1的格点设置已经确保一个格点只能预测1个类，但是由于中心点定位的偏差及相邻物体的原因，会出现多个格点预测了同一个物体的现象
可以借鉴YOLOv2 将分类结果绑定到bbox上，现在是1个预测位置预测：2个bbox及1个类别，改为预测2个bbox及2个类别

YOLOv1 与 Fast R-CNN 在预测结果上差异？

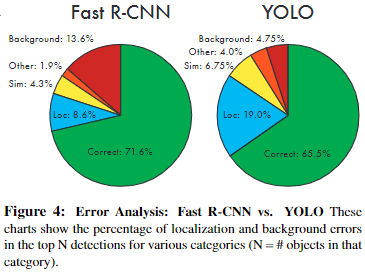
YOLOv1 的 Localization 错误率更高，直接对位置进行回归，确实不如滑窗式的检测方式准确率高
YOLOv1 对于背景的误检率更低，由于 Yolo 在推理时，可以“看到”整张图片，所以能够更好的区分背景与待测物体

YOLOv1 的预测框位置时，模型为什么不稳定？

模型不稳定，尤其是早期迭代时。大多不稳定来自预测框中心 $(g_x,g_y)$ 。 $b_x,b_y$ 是先验框的中心位置， $b_w,b_h$ 为先验框的宽高，计算如下 $g_x=\left(t_{x} * \Delta x \right)+b_{x}, g_y=\left(t_{y} * \Delta y \right)+b_{y}$
$\Delta x,\Delta y$ 是要学习的参数，如果 $\Delta x=1$ 时， $g^x=t^{x} +b^{x}$ ，预测的位置右移一个锚箱宽度； $\Delta x=-1$ 时， $g^x=t^{x} - b^{x}$ ，预测的位置左移相同的宽度。该公式无约束，因此预测边框的中心可能出现在任何位置，训练早期阶段不容易稳定。YOLOv2调整了预测公式，将预测边框的中心约束在特定gird网格内，使得训练更稳定，参考：YOLOv2论文中的直接位置预测(Directlocationprediction)

YOLOv1的缺点？

因为YOLO中每个cell只预测两个bbox和一个类别，这就限制了能预测重叠或邻近物体的数量(论文至多49个目标)，比如说两个物体的中心点都落在这个cell中，但是这个cell只能预测一个类别
不像FasterRCNN一样预测offset，YOLO是直接预测bbox的位置的，这就增加了训练的难度，参考：YOLOv1的预测框位置时，模型为什么不稳定
YOLO是根据训练数据来预测bbox的，但是当测试数据中的物体出现了训练数据中的物体没有的长宽比时，YOLO的泛化能力低

什么是边框回归(Bounding Box Regression)?

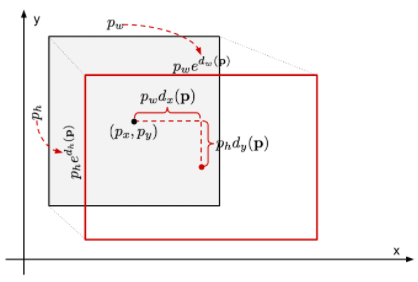
使用4维向量 (x, y, w, h)表示一个边框，图中的 P、G、T 分别表示 Proposal (获选框、先验框)、预测框、真实框，边框回归的目的：寻找一种关系使得输入原始的窗口 P 经过映射得到一个“跟真实框 T 更接近的”G，即给定 $\left(P_{x}, P_{y}, P_{w}, P_{h}\right)$ ，寻找映射关系 f，使得 $\begin{array}{l} f\left([P_{x}, P_{y}, P_{w}, P_{h}]+[G_{x}, G_{y}, G_{w}, G_{h}]\right)=\left(\hat{G}_{x}, \hat{G}_{y}, \hat{G}_{w}, \hat{G}_{h}\right) \\ \left(\hat{G}_{x}, \hat{G}_{y}, \hat{G}_{w}, \hat{G}_{h}\right) \approx\left(G_{x}, G_{y}, G_{w}, G_{h}\right) \end{array}$
主要包括2个过程，分别是平移及尺度变换。图中P、G、T这3个框表示为 $P=\left(b^{x}, b^{y}, b^{w}, b^{h}\right), \quad T=\left(t^{x}, t^{y}, t^{w}, t^{h}\right), \quad G=\left(g^{x}, g^{y}, g^{w}, g^{l^{2}}\right)$ ，边框回归的目的是基于先验框 $P$ 及真实框 $T$ 的信息，得到回归参数，使得先验框 $P$ 经过回归参数计算后，得到的预测框 $\hat{G}$ 更接近真实框T，回归参数共4个，分别是平移变换2个( $\Delta x,\Delta y$ )+尺度变换2个( $\Delta w,\Delta h$ )
平移变换：将先验框中心向真实框中心移动的过程，等式右边是框的更新过程，因为 $b^w,b^h$ 是图像宽高，是个常量，所以不需要求导计算更新。实际模型推理时，输出 $\Delta x$ ，则其预测框中心 x 位置为 $\Delta x*b^x$ $\Delta x=\left(t^{x}-b^{x}\right) / b^{w} \Rightarrow g^{x}=b^{x}+\Delta x\\ \Delta y=\left(t^{y}-b^{y}\right) / b^{h} \Rightarrow g^{y}=b^{y}+\Delta y$
尺度变换：将先验框尺寸向真实框尺寸变换的过程 $\Delta w=\log \left(t^{w} / b^{w}\right) \Rightarrow g^{w}=b^{w} \Delta w\\ \Delta h=\log \left(t^{h} / b^{h}\right) \Rightarrow g^{h}=b^{h} \Delta h$
这里的 $\Delta x,\Delta y,\Delta w,\Delta h$ 是回归过程需要学习的参数，这些参数可以根据先验框还原为预测框，并根据预测框与真实框的差距计算损失，得到损失使用随机梯度下降 (SGD) 等优化函数，更新 $\Delta x,\Delta y,\Delta w,\Delta h$