E01 - 图像复原与重建

发表于 2022-06-15 更新于 2025-01-18 分类于 3-编程实践， E-OpenCV ， OpenCV使用指南阅读次数：本文字数： 26k 阅读时长 ≈ 23 分钟

图像因为相机或拍摄存在噪声、缺失和抖动问题，导致成像有噪点、不清晰，如果噪声和抖动是有规律的，那么可以通过特定的方法去除这些干扰，复原或修复图像

什么是图像噪声？

数字图像中的噪声源主要来自图像获取和传输过程。在获取图像时，光照水平和传感器温度影响图像中的噪声。在传输图像时，传输信道中的干扰对图像产生污染

什么是加性噪声？

一般指热噪声、散弹噪声等，它们与信号的关系是相加，不管有没有信号，噪声都存在，即将一个固定大小的随机数加到数据上，结果可以表示为原始数据加上噪声。它具有独立性和相等方差性，常见于无监督学习，如高斯、瑞利、爱尔兰噪声等

什么是乘性噪声？

一般由信道不理想引起，它们与信号的关系是相乘，信号在它在，信号不在他也就不在，即将数据乘以一个随机数，结果可以表示为原始数据乘上噪声。它常常表现为数据的变化率随机变化，如合成孔径雷达、超声波、激光等相干图像系统当中

# 生成乘性噪声
img_height,img_width,img_channels=image.shape
gauss = np.random.randn(img_height,img_width,img_channels)
#给图片添加speckle噪声
speckle_noisy_img = image + image * gauss
#归一化图像的像素值
speckle_noisy_img = np.clip(speckle_noisy_img,a_min=0,a_max=255)

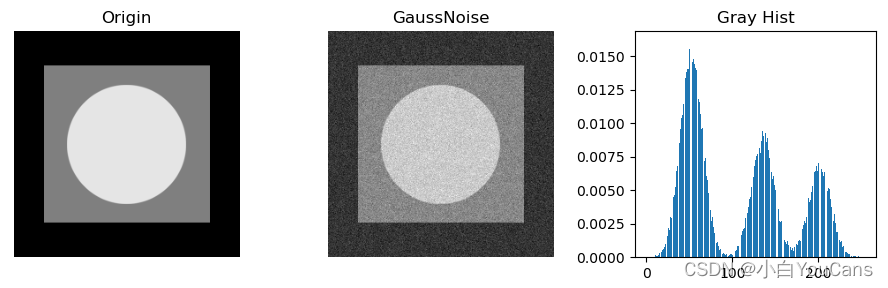
什么是高斯噪声？

高斯噪声中空间域和频率域中都很方便进行数学处理，因而得到了广泛的应用

img = cv2.imread("../images/Fig0503.tif", 0)  # flags=0 读取为灰度图像
# 加入高斯噪声
mu, sigma = 0.0, 20.0
noiseGause = np.random.normal(mu, sigma, img.shape)
imgGaussNoise = img + noiseGause
imgGaussNoise = np.uint8(cv2.normalize(imgGaussNoise, None, 0, 255, cv2.NORM_MINMAX))

什么是瑞利噪声？

瑞利噪声概率密度分布到原点的距离及密度的基本形状右偏

img = cv2.imread("../images/Fig0503.tif", 0)  # flags=0 读取为灰度图像
# 加入瑞利噪声
a = 30.0
noiseRayleigh = np.random.rayleigh(a, size=img.shape)
imgRayleighNoise = img + noiseRayleigh
imgRayleighNoise = np.uint8(cv2.normalize(imgRayleighNoise, None, 0, 255, cv2.NORM_MINMAX))

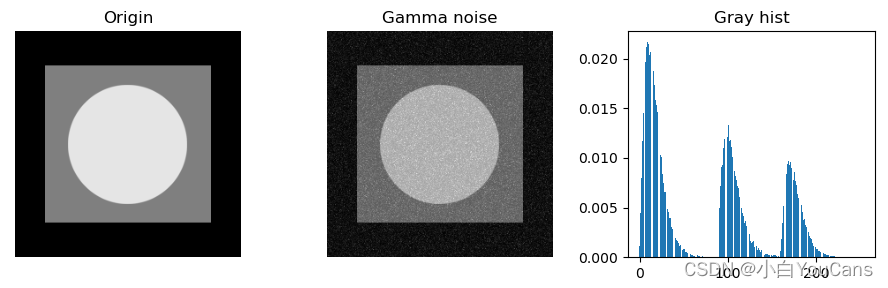
什么是爱尔兰噪声？

也称伽马噪声

img = cv2.imread("../images/Fig0503.tif", 0)  # flags=0 读取为灰度图像
a, b = 10.0, 2.5
noiseGamma = np.random.gamma(shape=b, scale=a, size=img.shape)
imgGammaNoise = img + noiseGamma
imgGammaNoise = np.uint8(cv2.normalize(imgGammaNoise, None, 0, 255, cv2.NORM_MINMAX))

什么是指数噪声？

指数噪声是爱尔兰噪声在 b=1 时的特殊情况

img = cv2.imread("../images/Fig0503.tif", 0)  # flags=0 读取为灰度图像
a = 10.0
noiseExponent = np.random.exponential(scale=a, size=img.shape)
imgExponentNoise = img + noiseExponent
imgExponentNoise = np.uint8(cv2.normalize(imgExponentNoise, None, 0, 255, cv2.NORM_MINMAX))

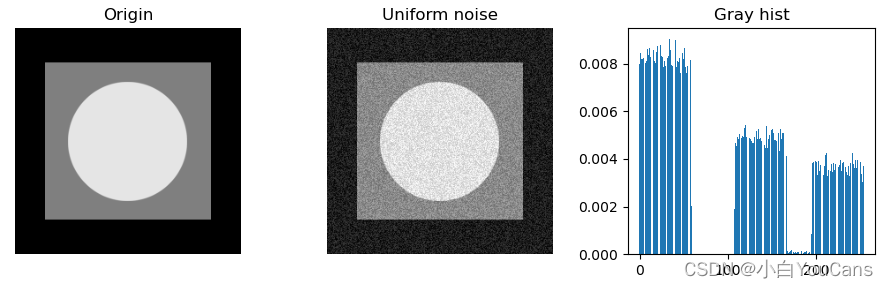
什么是均匀噪声？

使用 uniform 产生

img = cv2.imread("../images/Fig0503.tif", 0)  # flags=0 读取为灰度图像
mean, sigma = 10, 100
a = 2 * mean - np.sqrt(12 * sigma)  # a = -14.64
b = 2 * mean + np.sqrt(12 * sigma)  # b = 54.64
noiseUniform = np.random.uniform(a, b, img.shape)
imgUniformNoise = img + noiseUniform
imgUniformNoise = np.uint8(cv2.normalize(imgUniformNoise, None, 0, 255, cv2.NORM_MINMAX))

什么是椒盐噪声？

就像盐粒或胡椒粒那样随机地分布在整个图像上，因此称为椒盐噪声，也称为双极冲击噪声

img = cv2.imread("../images/Fig0503.tif", 0)  # flags=0 读取为灰度图像
ps, pp = 0.05, 0.02
mask = np.random.choice((0, 0.5, 1), size=img.shape[:2], p=[pp, (1-ps-pp), ps])
imgChoiceNoise = img.copy()
imgChoiceNoise[mask==1] = 255
imgChoiceNoise[mask==0] = 0

什么是泊松噪声？

符合泊松分布的噪声模型，泊松分布适合于描述单位时间内随机事件发生的次数的概率分布，如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA 序列的变异数、放射性原子核的衰变数等等

# 生成泊松噪声
#计算图像像素的分布范围
vals = len(np.unique(image))
vals = 2 ** np.ceil(np.log2(vals))
#给图片添加泊松噪声
poisson_noisy_img = np.random.poisson(image * vals) / float(vals)

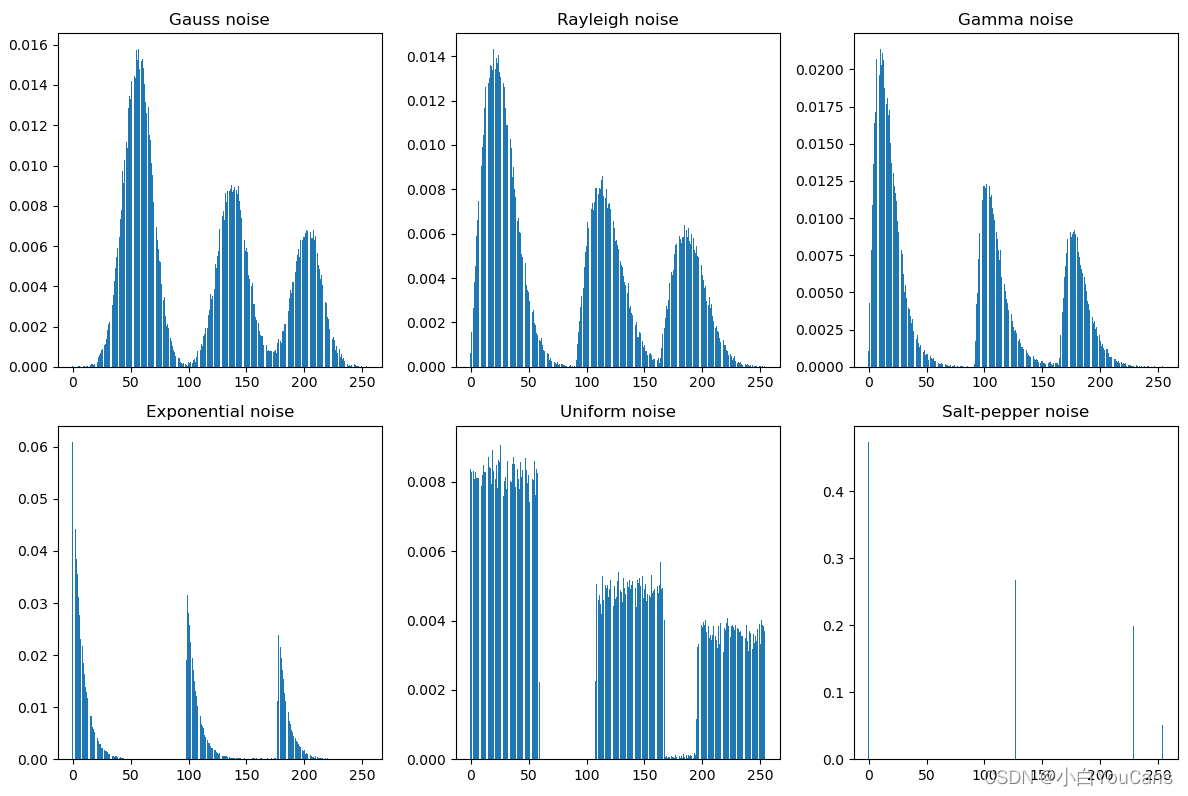
常见噪声的模拟场景？

高斯噪声：常用于电子电路及传感器噪声（光照不足和 / 或高温引起）等因素所导致噪声的建模；
瑞利噪声：常用于距离成像中的噪声建模；
指数噪声和伽马噪声：常用于激光成像中的噪声建模；
冲激噪声：常用于在成像期间的快速瞬变（如开关故障）的噪声建模；
均匀噪声：是对实际情况最基本描述，也是数字图像处理中各种随机数发生器的基础

什么是算术平均滤波器？

算术平均滤波器是最简单的均值滤波器，与空间域滤波中的盒式滤波器相同，即取一个固定大小窗口内的平均像素代替该像素值

img = cv2.imread("../images/Fig0507b.tif", 0)  # flags=0 读取为灰度图像
kSize = (3,3)
kernalMean = np.ones(kSize, np.float32) / (kSize[0]*kSize[1])  # 生成归一化盒式核
imgConv1 = cv2.filter2D(img, -1, kernalMean)  # cv2.filter2D 方法
kSize = (5,5)
imgConv3 = cv2.boxFilter(img, -1, kSize)  # cv2.boxFilter 方法 (默认normalize=True)

什么是几何平均滤波器？

选择一个窗口，求取窗口内的几何平均值作为该位置像素值

img = cv2.imread("../images/Fig0507b.tif", 0)  # flags=0 读取为灰度图像
img_h = img.shape[0]
img_w = img.shape[1]
# 算术平均滤波 (Arithmentic mean filter)
kSize = (3,3)
kernalMean = np.ones(kSize, np.float32) / (kSize[0]*kSize[1])  # 生成归一化盒式核
imgAriMean = cv2.filter2D(img, -1, kernalMean)
# 几何均值滤波器 (Geometric mean filter)
m, n = 3, 3
order = 1/(m*n)
kernalMean = np.ones((m,n), np.float32)  # 生成盒式核
hPad = int((m-1) / 2)
wPad = int((n-1) / 2)
imgPad = np.pad(img.copy(), ((hPad, m-hPad-1), (wPad, n-wPad-1)), mode="edge")
imgGeoMean = img.copy()
for i in range(hPad, img_h + hPad):
	for j in range(wPad, img_w + wPad):
		prod = np.prod(imgPad[i-hPad:i+hPad+1, j-wPad:j+wPad+1]*1.0)
		imgGeoMean[i-hPad][j-wPad] = np.power(prod, order)

什么是谐波平均滤波器？

谐波平均滤波器既能处理盐粒噪声（白色噪点），又能处理类似于高斯噪声的其他噪声，但不能处理胡椒噪声（黑色噪点）

img = cv2.imread("../images/Fig0507b.tif", 0)  # flags=0 读取为灰度图像
img_h,img_w = img.shape[0],img.shape[1]
# 算术平均滤波 (Arithmentic mean filter)
kSize = (3, 3)
kernalMean = np.ones(kSize, np.float32) / (kSize[0]*kSize[1])  # 生成归一化盒式核
imgAriMean = cv2.filter2D(img, -1, kernalMean)
# 谐波平均滤波器 (Harmonic mean filter)
m, n = 3, 3
order = m * n
kernalMean = np.ones((m,n), np.float32)  # 生成盒式核
hPad = int((m-1) / 2)
wPad = int((n-1) / 2)
imgPad = np.pad(img.copy(), ((hPad, m-hPad-1), (wPad, n-wPad-1)), mode="edge")
epsilon = 1e-8
imgHarMean = img.copy()
for i in range(hPad, img_h + hPad):
	for j in range(wPad, img_w + wPad):
		sumTemp = np.sum(1.0 / (imgPad[i-hPad:i+hPad+1, j-wPad:j+wPad+1] + epsilon))
		imgHarMean[i-hPad][j-wPad] = order / sumTemp

什么是反谐波平均滤波器？

反谐波平均滤波器适用于降低或消除椒盐噪声

img = cv2.imread("../images/Fig0508a.tif", 0)  # flags=0 读取为灰度图像
img_h = img.shape[0]
img_w = img.shape[1]
m, n = 3, 3
order = m * n
kernalMean = np.ones((m,n), np.float32)  # 生成盒式核
hPad = int((m-1) / 2)
wPad = int((n-1) / 2)
imgPad = np.pad(img.copy(), ((hPad, m-hPad-1), (wPad, n-wPad-1)), mode="edge")
Q = 1.5  # 反谐波平均滤波器 阶数
epsilon = 1e-8
imgHarMean = img.copy()
imgInvHarMean = img.copy()
for i in range(hPad, img_h + hPad):
	for j in range(wPad, img_w + wPad):
		# 谐波平均滤波器 (Harmonic mean filter)
		sumTemp = np.sum(1.0 / (imgPad[i-hPad:i+hPad+1, j-wPad:j+wPad+1] + epsilon))
		imgHarMean[i-hPad][j-wPad] = order / sumTemp
		# 反谐波平均滤波器 (Inv-harmonic mean filter)
		temp = imgPad[i-hPad:i+hPad+1, j-wPad:j+wPad+1] + epsilon
		imgInvHarMean[i-hPad][j-wPad] = np.sum(np.power(temp, (Q+1))) / np.sum(np.power(temp, Q) + epsilon)

什么是统计排序滤波器？

统计排序滤波器是空间滤波器，其响应是基于滤波器邻域中的像素值的顺序，排序结果决定了滤波器的输出

统计排序包括中值滤波器、最大值滤波器、最小值滤波器、中点滤波器和修正阿尔法均值滤波器

img = cv2.imread("../images/Fig0508a.tif", 0)  # flags=0 读取为灰度图像
img_h,img_w = img.shape[0],img.shape[1]
m, n = 3, 3
kernalMean = np.ones((m, n), np.float32)  # 生成盒式核
# 边缘填充
hPad = int((m-1) / 2)
wPad = int((n-1) / 2)
imgPad = np.pad(img.copy(), ((hPad, m-hPad-1), (wPad, n-wPad-1)), mode="edge")
imgMedianFilter = np.zeros(img.shape)  # 中值滤波器
imgMaxFilter = np.zeros(img.shape)  # 最大值滤波器
imgMinFilter = np.zeros(img.shape)  # 最小值滤波器
imgMiddleFilter = np.zeros(img.shape)  # 中点滤波器
for i in range(img_h):
	for j in range(img_w):
		# # 1. 中值滤波器 (median filter)
		pad = imgPad[i:i+m, j:j+n]
		imgMedianFilter[i, j] = np.median(pad)
		# # 2. 最大值滤波器 (maximum filter)
		pad = imgPad[i:i+m, j:j+n]
		imgMaxFilter[i, j] = np.max(pad)
		# # 3. 最小值滤波器 (minimum filter)
		pad = imgPad[i:i+m, j:j+n]
		imgMinFilter[i, j] = np.min(pad)
		# # 4. 中点滤波器 (middle filter)
		pad = imgPad[i:i+m, j:j+n]
		imgMiddleFilter[i, j] = int(pad.max()/2 + pad.min()/2)

什么是修正阿尔法均值滤波器？

修正阿尔法均值滤波器也属于统计排序滤波器，其思想类似于比赛中去掉最高分和最低分后计算平均分的方法。取固定大小的窗口，去掉 d 个最低和 d 个最高，剩下元素的平均作为输出结果

img = cv2.imread("../images/Fig0507b.tif", 0)  # flags=0 读取为灰度图像
img_h = img.shape[0]
img_w = img.shape[1]
m, n = 5, 5
kernalMean = np.ones((m, n), np.float32)  # 生成盒式核
# 边缘填充
hPad = int((m-1) / 2)
wPad = int((n-1) / 2)
imgPad = np.pad(img.copy(), ((hPad, m-hPad-1), (wPad, n-wPad-1)), mode="edge")
imgAlphaFilter0 = np.zeros(img.shape)
imgAlphaFilter1 = np.zeros(img.shape)
imgAlphaFilter2 = np.zeros(img.shape)
for i in range(img_h):
	for j in range(img_w):
		# 邻域 m * n
		pad = imgPad[i:i+m, j:j+n]
		padSort = np.sort(pad.flatten())  # 对邻域像素按灰度值排序
		d = 1
		sumAlpha = np.sum(padSort[d:m*n-d-1])  # 删除 d 个最大灰度值, d 个最小灰度值
		imgAlphaFilter0[i, j] = sumAlpha / (m*n-2*d)  # 对剩余像素进行算术平均
		d = 2
		sumAlpha = np.sum(padSort[d:m*n-d-1])
		imgAlphaFilter1[i, j] = sumAlpha / (m*n-2*d)
		d = 4
		sumAlpha = np.sum(padSort[d:m*n-d-1])
		imgAlphaFilter2[i, j] = sumAlpha / (m*n-2*d)

什么是自适应局部降噪滤波器？

前述滤波器直接应用到图像处理，并未考虑图像本身的特征。自适应滤波器的特性根据 m∗n 矩形邻域 Sxy 定义的滤波区域内的图像的统计特性变化。通常，自适应滤波器的性能优于前述的滤波器，但滤波器的复杂度和计算量也更大

img = cv2.imread("../images/Fig0507b.tif", 0)  # flags=0 读取为灰度图像
hImg,wImg = img.shape[0],img.shape[1]
m, n = 5, 5
imgAriMean = cv2.boxFilter(img, -1, (m, n))  # 算术平均滤波
# 边缘填充
hPad = int((m-1) / 2)
wPad = int((n-1) / 2)
imgPad = np.pad(img.copy(), ((hPad, m-hPad-1), (wPad, n-wPad-1)), mode="edge")
# 估计原始图像的噪声方差 sigmaEta
mean, stddev = cv2.meanStdDev(img)
sigmaEta = stddev ** 2
print(sigmaEta)
# 自适应局部降噪
epsilon = 1e-8
imgAdaLocal = np.zeros(img.shape)
for i in range(hImg):
	for j in range(wImg):
		pad = imgPad[i:i+m, j:j+n]  # 邻域 Sxy, m*n
		gxy = img[i,j]  # 含噪声图像的像素点
		zSxy = np.mean(pad)  # 局部平均灰度
		sigmaSxy = np.var(pad)  # 灰度的局部方差
		rateSigma = min(sigmaEta / (sigmaSxy + epsilon), 1.0)  # 加性噪声假设：sigmaEta/sigmaSxy < 1
		imgAdaLocal[i, j] = gxy - rateSigma * (gxy - zSxy)

什么是自适应中值滤波器？

中值滤波器的窗口尺寸是固定大小不变的，不能同时兼顾去噪和保护图像的细节，在噪声的密度较小时的性能较好，当噪声概率较高时的性能就会劣化
自适应中值滤波器根据预先设定的条件，在滤波的过程中动态改变滤波器的窗口尺寸大小；进一步地，根据条件判断当前像素是否噪声，由此决定是否用邻域中值替换当前像素

自适应中值滤波器可以处理较大概率的脉冲噪声，平滑非脉冲噪声，尽可能保护图像细节信息，避免图像边缘的细化或者粗化

img = cv2.imread("../images/Fig0514a.tif", 0)  # flags=0 读取为灰度图像
hImg,wImg = img.shape[0],img.shape[1]
smax = 7  # 允许最大窗口尺寸
m, n = smax, smax
imgAriMean = cv2.boxFilter(img, -1, (m, n))  # 算术平均滤波
# 边缘填充
hPad = int((m-1) / 2)
wPad = int((n-1) / 2)
imgPad = np.pad(img.copy(), ((hPad, m-hPad-1), (wPad, n-wPad-1)), mode="edge")
imgMedianFilter = np.zeros(img.shape)  # 中值滤波器
imgAdaMedFilter = np.zeros(img.shape)  # 自适应中值滤波器
for i in range(hPad, hPad+hImg):
	for j in range(wPad, wPad+wImg):
		# 1. 中值滤波器 (Median filter)
		ksize = 3
		k = int(ksize/2)
		pad = imgPad[i-k:i+k+1, j-k:j+k+1]  # 邻域 Sxy, m*n
		imgMedianFilter[i-hPad, j-wPad] = np.median(pad)
		# 2. 自适应中值滤波器 (Adaptive median filter)
		ksize = 3
		k = int(ksize/2)
		pad = imgPad[i-k:i+k+1, j-k:j+k+1]
		zxy = img[i-hPad][j-wPad]
		zmin = np.min(pad)
		zmed = np.median(pad)
		zmax = np.max(pad)
		if zmin < zmed < zmax:
			if zmin < zxy < zmax:
				imgAdaMedFilter[i-hPad, j-wPad] = zxy
			else:
				imgAdaMedFilter[i-hPad, j-wPad] = zmed
		else:
			while True:
				ksize = ksize + 2
				if zmin < zmed < zmax or ksize > smax:
					break
				k = int(ksize / 2)
				pad = imgPad[i-k:i+k+1, j-k:j+k+1]
				zmed = np.median(pad)
				zmin = np.min(pad)
				zmax = np.max(pad)
			if zmin < zmed < zmax or ksize > smax:
				if zmin < zxy < zmax:
					imgAdaMedFilter[i-hPad, j-wPad] = zxy
				else:
					imgAdaMedFilter[i-hPad, j-wPad] = zmed

%% 图像复原 %%

什么是图像复原？

图像复原是对图像退化的过程进行估计，并补偿退化过程造成的失真，以便获得未经退化的原始图像或原始图像的最优估值，从而改善图像质量的一种方法
典型的图像复原方法是根据图像退化的先验知识建立退化模型，如湍流导致的模糊、匀速运动导致的模糊，以退化模型为基础采用滤波等手段进行处理，使复原后的图像符合一定的准则，达到改善图像质量的目的
图像复原是沿着质量降低的逆过程来重现真实的原始图像，通过去模糊函数而去除图像模糊

运动模糊退化模型？

运动模糊是相机，物体，背景间相对运动造成的效果，通常由于长时间曝光或场景内的物体快速移动导致，在摄影中可以借助移动镜头追踪移动的物体来避

def motionBlur(image, degree=10, angle=45):
	image = np.array(image)
	center = (degree/2, degree/2)  # 旋转中心
	M = cv2.getRotationMatrix2D(center, angle, 1)  # 无损旋转
	kernel = np.diag(np.ones(degree) / degree)  # 运动模糊内核
	kernel = cv2.warpAffine(kernel, M, (degree, degree))
	blurred = cv2.filter2D(image, -1, kernel)  # 图像卷积
	blurredNorm = np.uint8(cv2.normalize(blurred, None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
	return blurredNorm
# 运动模糊图像
img = cv2.imread("../images/Fig0526a.tif", 0)  # flags=0 读取为灰度图像
imgBlur1 = motionBlur(img, degree=30, angle=45)
imgBlur2 = motionBlur(img, degree=40, angle=45)
imgBlur3 = motionBlur(img, degree=60, angle=45)

湍流模糊退化模型？

湍流是自然界中普遍存在的一种复杂的流动现象。物体通过湍流大气成像时，受到湍流效应的影响，出现光强闪烁、光束方向漂移、光束宽度扩展及接收面上相位的起伏，造成图像模糊和抖动，甚至扭曲变形

def getDegradedImg(image, Huv):  # 根据退化模型生成退化图像
	rows, cols = image.shape[:2]  # 图片的高度和宽度
	# (1) 中心化, centralized 2d array f(x,y) * (-1)^(x+y)
	mask = np.ones((rows, cols))
	mask[1::2, ::2] = -1
	mask[::2, 1::2] = -1
	imageCen = image * mask
	# (2) 快速傅里叶变换
	dftImage = np.zeros((rows, cols, 2), np.float32)
	dftImage[:, :, 0] = imageCen
	cv2.dft(dftImage, dftImage, cv2.DFT_COMPLEX_OUTPUT)  # 快速傅里叶变换 (rows, cols, 2)
	# (4) 构建 频域滤波器传递函数:
	Filter = np.zeros((rows, cols, 2), np.float32)  # (rows, cols, 2)
	Filter[:, :, 0], Filter[:, :, 1] = Huv, Huv
	# (5) 在频率域修改傅里叶变换: 傅里叶变换 点乘 滤波器传递函数
	dftFilter = dftImage * Filter
	# (6) 对修正傅里叶变换 进行傅里叶逆变换，并只取实部
	idft = np.ones((rows, cols), np.float32)  # 快速傅里叶变换的尺寸
	cv2.dft(dftFilter, idft, cv2.DFT_REAL_OUTPUT + cv2.DFT_INVERSE + cv2.DFT_SCALE)  # 只取实部
	# (7) 中心化, centralized 2d array g(x,y) * (-1)^(x+y)
	mask2 = np.ones(dftImage.shape[:2])
	mask2[1::2, ::2] = -1
	mask2[::2, 1::2] = -1
	idftCen = idft * mask2  # g(x,y) * (-1)^(x+y)
	# (8) 截取左上角，大小和输入图像相等
	imgDegraded = np.uint8(cv2.normalize(idftCen, None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
	# print(image.shape, dftFilter.shape, imgDegraded.shape)
	return imgDegraded
def turbulenceBlur(img, k=0.001):  # 湍流模糊传递函数
	# H(u,v) = exp(-k(u^2+v^2)^5/6)
	M, N = img.shape[1], img.shape[0]
	u, v = np.meshgrid(np.arange(M), np.arange(N))
	radius = (u - M//2)**2 + (v - N//2)**2
	kernel = np.exp(-k * np.power(radius, 5/6))
	return kernel
# 读取原始图像
img = cv2.imread("../images/Fig0525a.tif", 0)  # flags=0 读取为灰度图像
# 生成湍流模糊图像
HBlur1 = turbulenceBlur(img, k=0.001)  # 湍流模糊传递函数
imgBlur1 = getDegradedImg(img, HBlur1)  # 生成湍流模糊图像
HBlur2 = turbulenceBlur(img, k=0.0025)
imgBlur2 = getDegradedImg(img, HBlur2)
show_images([img,imgBlur1,imgBlur2])

湍流模糊退化图像的逆滤波？

湍流退化模型可以得到退化图像。使用该退化模型进行逆滤波，退化函数与生成退化图像所用的退化函数相反

def turbulenceBlur(img, k=0.001):  # 湍流模糊传递函数: H(u,v) = exp(-k(u^2+v^2)^5/6)
	M, N = img.shape[1], img.shape[0]
	u, v = np.meshgrid(np.arange(M), np.arange(N))
	radius = (u - M//2)**2 + (v - N//2)**2
	kernel = np.exp(-k * np.power(radius, 5/6))
	return kernel
def getDegradedImg(image, Huv, eps):  # 根据退化模型生成退化图像
	# (1) 傅里叶变换, 中心化
	fft = np.fft.fft2(image.astype(np.float32))  # 傅里叶变换
	fftShift = np.fft.fftshift(fft)  # 将低频分量移动到频域图像中心
	# (2) 在频率域修改傅里叶变换: 傅里叶变换 点乘 滤波器传递函数
	fftShiftFilter = fftShift * Huv  # Guv = Fuv * Huv
	# (3) 对修正傅里叶变换 进行傅里叶逆变换，逆中心化
	invShift = np.fft.ifftshift(fftShiftFilter)  # 将低频分量逆转换回图像四角
	imgIfft = np.fft.ifft2(invShift)  # 逆傅里叶变换，返回值是复数数组
	imgDegraded = np.uint8(cv2.normalize(np.abs(imgIfft), None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
	return imgDegraded
def ideaLPFilter(img, radius=10):  # 理想低通滤波器
	M, N = img.shape[1], img.shape[0]
	u, v = np.meshgrid(np.arange(M), np.arange(N))
	D = np.sqrt((u - M//2)**2 + (v - N//2)**2)
	kernel = np.zeros(img.shape[:2], np.float32)
	kernel[D <= radius] = 1
	return kernel
def inverseFilter(image, Huv, D0):  # 根据退化模型逆滤波
	# (1) 傅里叶变换, 中心化
	fft = np.fft.fft2(image.astype(np.float32))  # 傅里叶变换
	fftShift = np.fft.fftshift(fft)  # 将低频分量移动到频域图像中心
	# (2) 在频率域修改傅里叶变换: 傅里叶变换 点乘 滤波器传递函数
	if D0==0:
		fftShiftFilter = fftShift / Huv  # Guv = Fuv / Huv
	else:
		lpFilter = ideaLPFilter(image, radius=D0)
		fftShiftFilter = fftShift / Huv * lpFilter  # Guv = Fuv / Huv
	# (3) 对修正傅里叶变换 进行傅里叶逆变换，逆中心化
	invShift = np.fft.ifftshift(fftShiftFilter)  # 将低频分量逆转换回图像四角
	imgIfft = np.fft.ifft2(invShift)  # 逆傅里叶变换，返回值是复数数组
	imgRebuild = np.uint8(cv2.normalize(np.abs(imgIfft), None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
	return imgRebuild
# 读取原始图像
img = cv2.imread("../images/Fig0525a.tif", 0)  # flags=0 读取为灰度图像
# 生成湍流模糊图像
HTurb = turbulenceBlur(img, k=0.0025)
imgBlur = np.abs(getDegradedImg(img, HTurb, 0.0))
print(imgBlur.max(), imgBlur.min())
# 逆滤波
imgRebuild = inverseFilter(imgBlur, HTurb, 480)  # Huv 全滤波器
imgRebuild1 = inverseFilter(imgBlur, HTurb, D0=40) #在半径 D0 之外 Huv 截止
imgRebuild2 = inverseFilter(imgBlur, HTurb, D0=70)
imgRebuild3 = inverseFilter(imgBlur, HTurb, D0=100)
show_images([img,imgBlur,imgRebuild,imgRebuild1,imgRebuild2,imgRebuild3])

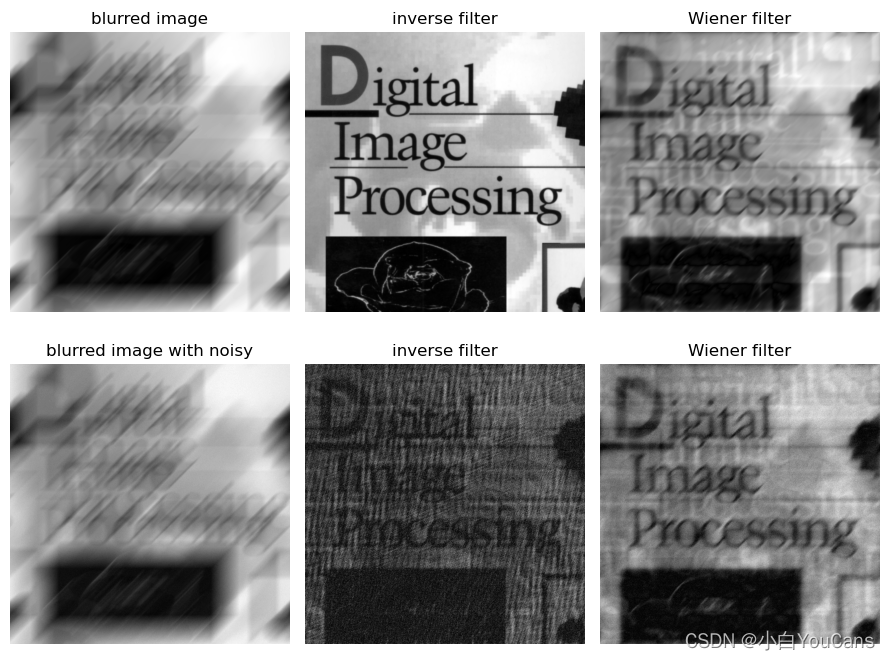
退化图像的维纳滤波（Wiener filter）?

最小均方差滤波由 1942 首先提出，是最早提出的线性图像复原方法，因此称为维纳滤波。用于处理运动滤波

对于不含噪声的运动模糊图像，在已知运动模糊退化模型和参数的前提下，使用逆滤波可以很好地复原退化图像，逆滤波的性能优于维纳滤波。但是，考虑实际退化图像往往含有一定水平的加性噪声，此时即使已知退化模型，逆滤波的后的噪声几乎掩盖了图像内容，而维纳滤波的结果则较好

def getMotionDsf(shape, angle, dist):
	xCenter = (shape[0] - 1) / 2
	yCenter = (shape[1] - 1) / 2
	sinVal = np.sin(angle * np.pi / 180)
	cosVal = np.cos(angle * np.pi / 180)
	PSF = np.zeros(shape)  # 点扩散函数
	for i in range(dist):  # 将对应角度上motion_dis个点置成1
		xOffset = round(sinVal * i)
		yOffset = round(cosVal * i)
		PSF[int(xCenter - xOffset), int(yCenter + yOffset)] = 1
	return PSF / PSF.sum()  # 归一化
def makeBlurred(image, PSF, eps):  # 对图片进行运动模糊
	fftImg = np.fft.fft2(image)  # 进行二维数组的傅里叶变换
	fftPSF = np.fft.fft2(PSF) + eps
	fftBlur = np.fft.ifft2(fftImg * fftPSF)
	fftBlur = np.abs(np.fft.fftshift(fftBlur))
	return fftBlur
def inverseFilter(image, PSF, eps):  # 逆滤波
	fftImg = np.fft.fft2(image)
	fftPSF = np.fft.fft2(PSF) + eps  # 噪声功率，这是已知的，考虑epsilon
	imgInvFilter = np.fft.ifft2(fftImg / fftPSF)  # 计算F(u,v)的傅里叶反变换
	imgInvFilter = np.abs(np.fft.fftshift(imgInvFilter))
	return imgInvFilter
def wienerFilter(input, PSF, eps, K=0.01):  # 维纳滤波，K=0.01
	fftImg = np.fft.fft2(input)
	fftPSF = np.fft.fft2(PSF) + eps
	fftWiener = np.conj(fftPSF) / (np.abs(fftPSF)**2 + K)
	imgWienerFilter = np.fft.ifft2(fftImg * fftWiener)
	imgWienerFilter = np.abs(np.fft.fftshift(imgWienerFilter))
	return imgWienerFilter
# 读取原始图像
img = cv2.imread("../images/Fig0526a.tif", 0)  # flags=0 读取为灰度图像
hImg, wImg = img.shape[:2]
# 不含噪声的运动模糊
PSF = getMotionDsf((hImg, wImg), 45, 100)  # 运动模糊函数
imgBlurred = np.abs(makeBlurred(img, PSF, 1e-6))  # 生成不含噪声的运动模糊图像
imgInvFilter = inverseFilter(imgBlurred, PSF, 1e-6)  # 逆滤波
imgWienerFilter = wienerFilter(imgBlurred, PSF, 1e-6)  # 维纳滤波
# 带有噪声的运动模糊
scale = 0.05  # 噪声方差
noisy = imgBlurred.std() * np.random.normal(loc=0.0, scale=scale, size=imgBlurred.shape)  # 添加高斯噪声
imgBlurNoisy = imgBlurred + noisy  # 带有噪声的运动模糊
imgNoisyInv = inverseFilter(imgBlurNoisy, PSF, scale)  # 对添加噪声的模糊图像进行逆滤波
imgNoisyWiener = wienerFilter(imgBlurNoisy, PSF, scale)  # 对添加噪声的模糊图像进行维纳滤波

约束最小二乘方滤波？

维纳滤波建立在退化函数和信噪比已知的前提下，这在实践中并不容易满足，约束最小二乘方滤波仅要求噪声方差和均值的知识或估计，这些参数通常可以由一幅给定的退化图像算出，因而具有更为广泛的应用。而且，维纳滤波是以最小化一个统计准则为基础，因此是平均意义上的最优，而约束最小二乘方滤波则对每幅图像都会产生最优估计

与维纳滤波相比，最小二乘方滤波对于高噪声和中等噪声处理效果更好，对于低噪声二者处理结果基本相同。当手工选择参数以取得更好的视觉效果时，约束最小二乘方滤波的效果有可能比维纳滤波的效果更好

def getMotionDsf(shape, angle, dist):
	xCenter = (shape[0] - 1) / 2
	yCenter = (shape[1] - 1) / 2
	sinVal = np.sin(angle * np.pi / 180)
	cosVal = np.cos(angle * np.pi / 180)
	PSF = np.zeros(shape)  # 点扩散函数
	for i in range(dist):  # 将对应角度上motion_dis个点置成1
		xOffset = round(sinVal * i)
		yOffset = round(cosVal * i)
		PSF[int(xCenter - xOffset), int(yCenter + yOffset)] = 1
	return PSF / PSF.sum()  # 归一化
def makeBlurred(image, PSF, eps):  # 对图片进行运动模糊
	fftImg = np.fft.fft2(image)  # 进行二维数组的傅里叶变换
	fftPSF = np.fft.fft2(PSF) + eps
	fftBlur = np.fft.ifft2(fftImg * fftPSF)
	fftBlur = np.abs(np.fft.fftshift(fftBlur))
	return fftBlur
def wienerFilter(input, PSF, eps, K=0.01):  # 维纳滤波，K=0.01
	fftImg = np.fft.fft2(input)
	fftPSF = np.fft.fft2(PSF) + eps
	fftWiener = np.conj(fftPSF) / (np.abs(fftPSF)**2 + K)
	imgWienerFilter = np.fft.ifft2(fftImg * fftWiener)
	imgWienerFilter = np.abs(np.fft.fftshift(imgWienerFilter))
	return imgWienerFilter
def getPuv(image):
	h, w = image.shape[:2]
	hPad, wPad = h - 3, w - 3
	pxy = np.array([[0, -1, 0], [-1, 4, -1], [0, -1, 0]])
	pxyPad = np.pad(pxy, ((hPad//2, hPad - hPad//2), (wPad//2, wPad - wPad//2)), mode='constant')
	fftPuv = np.fft.fft2(pxyPad)
	return fftPuv
def leastSquareFilter(image, PSF, eps, gamma=0.01):  # 约束最小二乘方滤波
	fftImg = np.fft.fft2(image)
	fftPSF = np.fft.fft2(PSF)
	conj = fftPSF.conj()
	fftPuv = getPuv(image)
	# absConj = np.abs(fftPSF) ** 2
	Huv = conj / (np.abs(fftPSF)**2 + gamma * (np.abs(fftPuv)**2))
	ifftImg = np.fft.ifft2(fftImg * Huv)
	ifftShift = np.abs(np.fft.fftshift(ifftImg))
	imgLSFilter = np.uint8(cv2.normalize(np.abs(ifftShift), None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
	return imgLSFilter
# # 读取原始图像
img = cv2.imread("../images/Fig0526a.tif", 0)  # flags=0 读取为灰度图像
hImg, wImg = img.shape[:2]
# 带有噪声的运动模糊
PSF = getMotionDsf((hImg, wImg), 45, 100)  # 运动模糊函数
imgBlurred = np.abs(makeBlurred(img, PSF, 1e-6))  # 生成不含噪声的运动模糊图像
scale = 0.01  # 噪声方差
noisy = imgBlurred.std() * np.random.normal(loc=0.0, scale=scale, size=imgBlurred.shape)  # 添加高斯噪声
imgBlurNoisy = imgBlurred + noisy  # 带有噪声的运动模糊
imgWienerFilter = wienerFilter(imgBlurNoisy, PSF, scale, K=0.01)  # 对含有噪声的模糊图像进行维纳滤波
imgLSFilter = leastSquareFilter(imgBlurNoisy, PSF, scale, gamma=0.01)  # 约束最小二乘方滤波

几何均值滤波？

几何均值滤波器是维纳滤波的推广，其传递函数由括号内幂次分别为 α 和 1 − α 的两个表达式组成

def getMotionDsf(shape, angle, dist):
	xCenter = (shape[0] - 1) / 2
	yCenter = (shape[1] - 1) / 2
	sinVal = np.sin(angle * np.pi / 180)
	cosVal = np.cos(angle * np.pi / 180)
	PSF = np.zeros(shape)  # 点扩散函数
	for i in range(dist):  # 将对应角度上motion_dis个点置成1
		xOffset = round(sinVal * i)
		yOffset = round(cosVal * i)
		PSF[int(xCenter - xOffset), int(yCenter + yOffset)] = 1
	return PSF / PSF.sum()  # 归一化
def makeBlurred(image, PSF, eps):  # 对图片进行运动模糊
	fftImg = np.fft.fft2(image)  # 进行二维数组的傅里叶变换
	fftPSF = np.fft.fft2(PSF) + eps
	fftBlur = np.fft.ifft2(fftImg * fftPSF)
	fftBlur = np.abs(np.fft.fftshift(fftBlur))
	return fftBlur
def wienerFilter(input, PSF, eps, K=0.01):  # 维纳滤波，K=0.01
	fftImg = np.fft.fft2(input)
	fftPSF = np.fft.fft2(PSF) + eps
	fftWiener = np.conj(fftPSF) / (np.abs(fftPSF)**2 + K)
	imgWienerFilter = np.fft.ifft2(fftImg * fftWiener)
	imgWienerFilter = np.abs(np.fft.fftshift(imgWienerFilter))
	return imgWienerFilter
def geometricMeanFilter(image, PSF, eps, K=1, alpha=1, beta=1):  # 几何均值滤波器
	fftImg = np.fft.fft2(image)
	fftPSF = np.fft.fft2(PSF)
	conj = fftPSF.conj()
	squarePSF = (fftPSF * conj).real
	Huv = np.power(conj / (squarePSF), alpha) * np.power(conj / (squarePSF + beta * K), 1-alpha)
	ifftImg = np.fft.ifft2(fftImg * Huv)
	ifftShift = np.abs(np.fft.fftshift(ifftImg))
	imgGMFilter = np.uint8(cv2.normalize(np.abs(ifftShift), None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
	return imgGMFilter
# # 读取原始图像
img = cv2.imread("../images/Fig0526a.tif", 0)  # flags=0 读取为灰度图像
hImg, wImg = img.shape[:2]
# 带有噪声的运动模糊
PSF = getMotionDsf((hImg, wImg), 45, 100)  # 运动模糊函数
imgBlurred = np.abs(makeBlurred(img, PSF, 1e-6))  # 生成不含噪声的运动模糊图像
scale = 0.01  # 噪声方差
noisy = imgBlurred.std() * np.random.normal(loc=0.0, scale=scale, size=imgBlurred.shape)  # 添加高斯噪声
imgBlurNoisy = imgBlurred + noisy  # 带有噪声的运动模糊
imgWienerFilter = wienerFilter(imgBlurNoisy, PSF, scale, K=0.01)  # 对含有噪声的模糊图像进行维纳滤波
imgGMFilter = geometricMeanFilter(imgBlurNoisy, PSF, scale, K=0.01, alpha=0.5, beta=1)  # 约束最小二乘方滤波
show_images([imgBlurNoisy,imgWienerFilter,imgGMFilter])
scale = 0.1  # 噪声方差
noisy = imgBlurred.std() * np.random.normal(loc=0.0, scale=scale, size=imgBlurred.shape)  # 添加高斯噪声
imgBlurNoisy = imgBlurred + noisy  # 带有噪声的运动模糊
imgWienerFilter = wienerFilter(imgBlurNoisy, PSF, scale, K=0.01)  # 维纳滤波
imgGMFilter = geometricMeanFilter(imgBlurNoisy, PSF, scale, K=0.01, alpha=0, beta=1)  # 约束最小二乘方滤波
show_images([imgBlurNoisy,imgWienerFilter,imgGMFilter])

%% 图像重建 %%

什么是图像的重建？

通过探测物体的投影数据，重建物体的实际内部构造
X 射线计算机断层成像的基本原理是：使用 X 射线从多个不同方向和角度对物体进行扫描，通过反投影算法获取物体内部结构的切片，堆叠这些切片就可以得到人体的三维表示

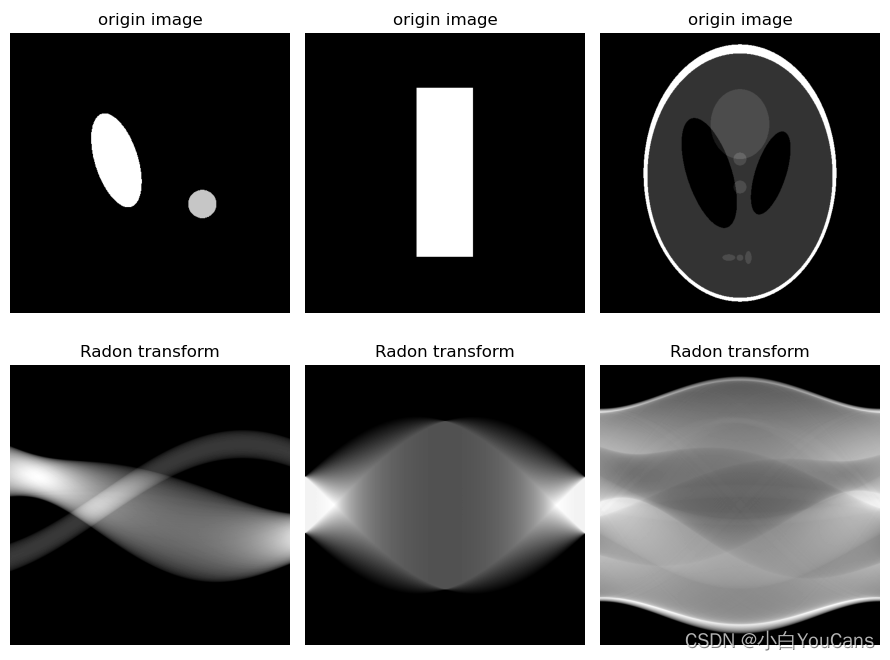
投影和雷登变换（Radon transform）？

雷登变换常被用于医学影像处理，利用反雷登变换可以进行三维图像重建

from scipy import ndimage
def discreteRadonTransform(image, steps):
	channels = image.shape[0]
	res = np.zeros((channels, channels), dtype=np.float32)
	for s in range(steps):
		rotation = ndimage.rotate(image, -s * 180/steps, reshape=False).astype(np.float32)
		res[:, s] = sum(rotation)
	return res
# # 读取原始图像
plt.figure(figsize=(9, 7))
fileImg = ["Fig0534a.tif", "Fig0534b.tif", "Fig0534c.tif"]  # 原始图像 文件名
for i in range(len(fileImg)):
	img = cv2.imread("../images/"+fileImg[i], flags=0)  # flags=0 读取为灰度图像
	imgRadon = discreteRadonTransform(img, img.shape[0])  # Radon 变换
	print(img.shape, imgRadon.shape)
	show_images([img,imgRadon])

雷登变换反投影重建图像？

反向投影是针对图像平面的基本几何元素而言的，图像平面点 m 的反投影是指在摄像机 P 的作用下具有像点 m 的所有空间点的集合

from scipy import ndimage
def discreteRadonTransform(image, steps):  # 离散雷登变换
	channels = image.shape[0]
	resRadon = np.zeros((channels, channels), dtype=np.float32)
	for s in range(steps):
		rotation = ndimage.rotate(image, -s * 180/steps, reshape=False).astype(np.float32)
		resRadon[:, s] = sum(rotation)
	return resRadon
def inverseRadonTransform(image, steps):  # 雷登变换反投影
	channels = image.shape[0]
	res = np.zeros((steps, channels, channels))
	for s in range(steps):
		expandDims = np.expand_dims(image[:, s], axis=0)
		repeat = expandDims.repeat(channels, axis=0)
		res[s] = ndimage.rotate(repeat, s * 180/steps, reshape=False).astype(np.float32)
	invRadon = np.sum(res, axis=0)
	return invRadon
# 读取原始图像
img1 = cv2.imread("../images/Fig0534a.tif", 0)  # flags=0 读取为灰度图像
img2 = cv2.imread("../images/Fig0534c.tif", 0)
# 雷登变换
imgRadon1 = discreteRadonTransform(img1, img1.shape[0])  # Radon 变换
imgRadon2 = discreteRadonTransform(img2, img2.shape[0])
# 雷登变换反投影
imgInvRadon1 = inverseRadonTransform(imgRadon1, imgRadon1.shape[0])
imgInvRadon2 = inverseRadonTransform(imgRadon2, imgRadon2.shape[0])

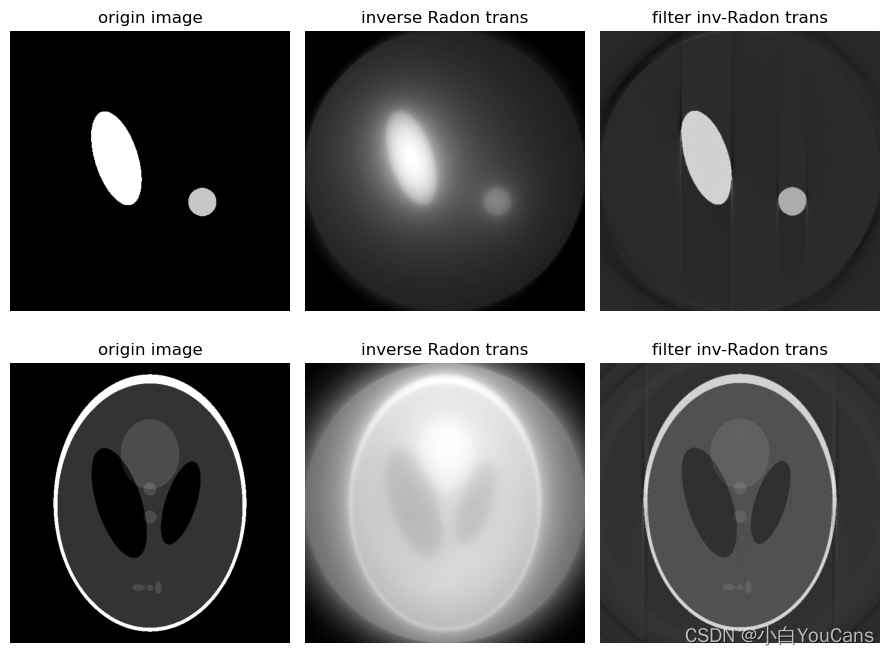
滤波反投影重建图像？

直接由正弦图得到反投影图像，会存在严重的模糊，这是早期 CT 系统所存在的问题

傅立叶中心切片定理表明，投影的一维傅立叶变换是得到投影区域的二维傅立叶变换的切片。滤波反投影重建算法在反投影前将每一个采集投影角度下的投影进行卷积处理，从而改善点扩散函数引起的形状伪影，有效地改善了重建的图像质量

from scipy import ndimage
def discreteRadonTransform(image, steps):  # 离散雷登变换
	channels = image.shape[0]
	resRadon = np.zeros((channels, channels), dtype=np.float32)
	for s in range(steps):
		rotation = ndimage.rotate(image, -s * 180/steps, reshape=False).astype(np.float32)
		resRadon[:, s] = sum(rotation)
	return resRadon
def inverseRadonTransform(image, steps):  # 雷登变换反投影重建图像
	channels = image.shape[0]
	backproject = np.zeros((steps, channels, channels))
	for s in range(steps):
		expandDims = np.expand_dims(image[:, s], axis=0)
		repeat = expandDims.repeat(channels, axis=0)
		backproject[s] = ndimage.rotate(repeat, s * 180/steps, reshape=False).astype(np.float32)
	invRadon = np.sum(backproject, axis=0)
	return invRadon
def SLFilter(N, d):  # SL 滤波器, Sinc 函数对斜坡滤波器进行截断
	filterSL = np.zeros((N,))
	for i in range(N):
		filterSL[i] = - 2 / (np.pi**2 * d**2 * (4 * (i-N/2)**2 - 1))
	return filterSL
def filterInvRadonTransform(image, steps):  # 滤波反投影重建图像
	channels = len(image[0])
	backproject = np.zeros((steps, channels, channels))  # 反投影
	filter = SLFilter(channels, 1)  # SL 滤波器
	for s in range(steps):
		value = image[:, s]  # 投影值
		valueFiltered = np.convolve(filter, value, "same")  # 投影值和 SL 滤波器进行卷积
		filterExpandDims = np.expand_dims(valueFiltered, axis=0)
		filterRepeat = filterExpandDims.repeat(channels, axis=0)
		backproject[s] = ndimage.rotate(filterRepeat, s * 180/steps, reshape=False).astype(np.float32)
	filterInvRadon = np.sum(backproject, axis=0)
	return filterInvRadon
# 读取原始图像
img1 = cv2.imread("../images/Fig0534a.tif", 0)  # flags=0 读取为灰度图像
img2 = cv2.imread("../images/Fig0534c.tif", 0)
# 雷登变换
imgRadon1 = discreteRadonTransform(img1, img1.shape[0])  # Radon 变换
imgRadon2 = discreteRadonTransform(img2, img2.shape[0])
# 雷登变换反投影重建图像
imgInvRadon1 = inverseRadonTransform(imgRadon1, imgRadon1.shape[0])
imgInvRadon2 = inverseRadonTransform(imgRadon2, imgRadon2.shape[0])
# 滤波反投影重建图像
imgFilterInvRadon1 = filterInvRadonTransform(imgRadon1, imgRadon1.shape[0])
imgFilterInvRadon2 = filterInvRadonTransform(imgRadon2, imgRadon2.shape[0])

参考：