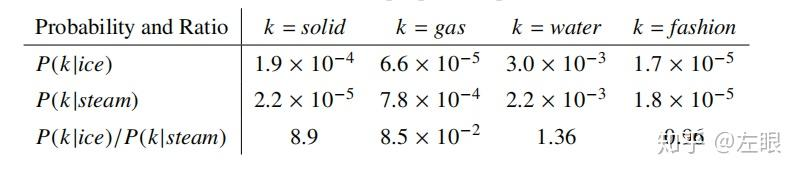GloVe

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 5.7k 阅读时长 ≈ 5 分钟

类似 word 2 vec，GloVe 也是一种词向量的训练方式，但是不同于 word 2 vec 只使用一个 windows 内的上下文生成词向量，GloVe
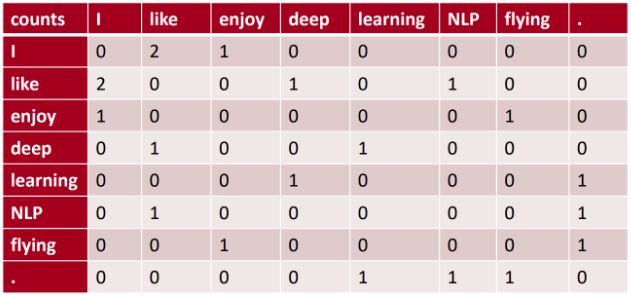
通过拟合共现矩阵的概率比进行网络学习，使用了全局统计信息，所以语义效果更佳

什么是 GloVe ？

  • 类似 word 2 vec，GloVe 也是一种词向量的训练方式，但是不同于 word 2 vec 只使用一个 windows 内的上下文生成词向量，GloVe 使用了全局统计信息，所以语义效果更佳
  • GloVe 的训练样本是共现矩阵，每次从共现矩阵拿两个词进行拟合，而 word 2 Vec 是随机找一定窗口大小的文本进行拟合

GloVe 上关于共现矩阵的作用？

  • 假设现有共现矩阵 X，其中 XijX_{ij} 表示单词 i 和单词 j 在给定长度窗口中出现的次数，Xi=∑kXikX_i=\sum_k X_{ik} 表示所有单词和单词 i 在上下文窗口出现的次数只和，Pij=P(j∣i)=XijXiP_{ij}=P (j|i)=\frac{X_{ij}}{X_i} 表示单词 j 和单词 i 共现上下文窗口的概率
  • 上图给出不同 i 情况下，j 出现的概率及其几率。当 k=solid 时，其相比 steam 与 ice 更接近，所以 P(k∣ice)P(k|ice) 会比 P(k∣steam)P(k|steam) 更大，所以其比值大于 1。而 k=fashion 时，情况相反，所以其比值小于 1。所以 Glove 认为对比共现概率与概率比率更能反映出词的相关性

GloVe 的目标函数？

  • 已知共现矩阵的概率比值很重要，如果我们的词向量能和共现矩阵反应相同的关系，那么词向量就是有价值的。现目标函数如下，其中 w∈Rd{w}\in R^{d} 是词向量、w~∈Rd\tilde{w}\in R^{d} 是背景词向量，x~k\tilde{x}_k 是 k 的词向量，Pij=P(j∣i)=XijXiP_{ij}=P (j|i)=\frac{X_{ij}}{X_i} 表示单词 j 和单词 i 共现上下文窗口的概率。右边是共现矩阵求得，我们现在目的是如何通过这 3 个词向量去求解共现矩阵的概率比值。注意这里每一步变现操作都是出于作者的数学直觉，目的是得到一个便于优化的 loss 函数形

F(wi,wj,x~k)=PikPjk,(4)F(w_{i},w_{j},\tilde{x}_{k})=\frac{P_{ik}}{P_{jk}},\quad\quad\quad\quad\quad\quad\quad(4)

  • (1) 考虑到词向量在线性空间，因此可以进行差值计

F(wi−wj,w~k)=PikPjk,(5)F(w_i-w_j,\widetilde{w}_k)=\frac{P_{ik}}{P_{jk}},\quad\quad\quad\quad\quad\quad\quad(5)

  • (2) 进一步，考虑右边是标量，左边 F 可以是复杂的参数函数（神经网络），可以点乘参

F((wi−wj)Twk~)=PikPjk,(6)F((w_i-w_j)^T\widetilde{w_k})=\frac{P_{ik}}{P_{jk}},\quad\quad\quad\quad\quad\quad\quad(6)

  • (3) 我们知道 X 是个对称矩阵，单词和上下文单词其实是相对的，也就是如果我们做如下变换：w↔wk~,X↔XTw\leftrightarrow\tilde{w_k},X\leftrightarrow X^T，目前公式不满足，于是要求函数 F 满足同态

F((wi−wj)Tw~k)=F(wiTw~k)F(wjTw~k),(7)F((w_i-w_j)^T\widetilde{w}_k)=\frac{F(w_i^T\widetilde{w}_k)}{F(w_j^T\widetilde{w}_k)},\quad\quad\quad(7)

  • (4) 组合公式 (6)，得到：$$F (w_i^T\tilde {w}k)=P{ik}=\frac{X_{ik}}{X_i},\quad(8)$$
  • (5) 令 F=exp，得到：$$w_i^T\widetilde {w}k=\log(P{ik})=\log(X_{ik})–\log(X_i),\quad\quad\quad\quad(9)$$
  • (6) 因为 log(Xi)log(X_i) 是跟 k 独立的，而左边只有与 k 相关部分，所以公式不满足对称性，所以左边加上以上内

wiTw~k+bi=log⁡(Xik),(10)w_i^T\widetilde{w}_k+b_i=\log(X_{ik}),\quad\quad\quad\quad\quad\quad(10)

  • (7) 但是公式 10 还是不满足对称性，于是我们针对 wkw_k 增加一个 bias term bkb_k，从而得到公式 1 的形

wiTw~k+bi+bk=log⁡(Xik),(1)w_i^T\widetilde{w}_k+b_i+b_k=\log(X_{ik}),\quad\quad\quad\quad\quad\quad(1)

  • (8) 损失函数：Glove 的目标是通过调整公式 (1) 左边参数，使得接近右边的标量，所以其损失函数定义如下，其中 f (x) 是权重系数，用于给哪些经常共现词的权重设置一个上限：$$\begin {array}{ll} J=\sum_{i,j=1}Vf(X_{ij})(w_iT\tilde{x}k+b_i+\tilde{b}j-log(X{ik})) \f(x)=\left{\begin{array}{cl}(x/x{\max})^\alpha&\quad\text{if}x<x_{\max}\1&\quad\text{otherwise}\end{array}\right.\end{array}$$

GloVe 的原理？

  • 根据 GloVe 共现矩阵的作用及目标函数，我们可以知道 Glove 是初始化词向量，然后使用词向量去计算拟合 log(Xik)log(X_{ik})，拟合完成时，词向量构造完

J=∑i,j=1Vf(Xij)(wiTx~k+bi+b~j−log(Xik))f(x)={(x/xmax⁡)αifx<xmax⁡1otherwise\begin{array}{ll}J=\sum_{i,j=1}^Vf(X_{ij})(w_i^T\tilde{x}_k+b_i+\tilde{b}_j-log(X_{ik})) \\f(x)=\left\{\begin{array}{cl}(x/x_{\max})^\alpha&\quad\text{if}x<x_{\max}\\1&\quad\text{otherwise}\end{array}\right.\end{array}

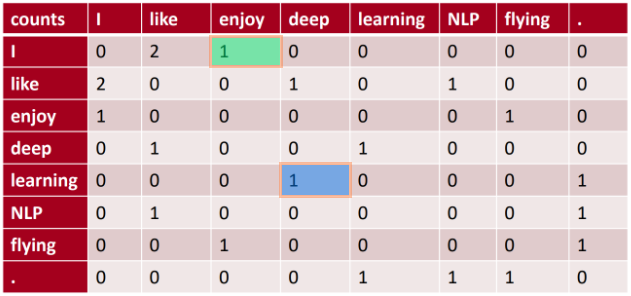
  • 比如假设上图的 like 与 enjoy 的 log(Xik)=log(1)=0log(X_{ik})=log(1)=0，则词向量往 0 去拟合
  • 注意：GloVe 的训练样本是共现矩阵，每次从共现矩阵拿两个词进行拟合，而 word 2 Vec 是随机找一定窗口大小的文本进行拟合

GloVe 的网络结构？

  • 无经典的网络层，只是 4 个可训练的张量计算，并通过拟合共现矩阵的概率比进行网络学习
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class GloVe(nn.Module):
	def __init__(self,dataset, embed_size=300, y_max=100, alpha=0.75):
		super().__init__()
		self.embed_size = embed_size
		self.y_max, self.alpha = y_max, alpha
		get_var_by_shape = lambda *shape: Parameter(torch.randn(*shape).mul(std).cuda(), requires_grad=True)
		# 以下是可训练的4个张量
		self.a_vecs=get_var_by_shape(dataset.n_words, self.embed_size)
		self.b_vecs=get_var_by_shape(dataset.n_words, self.embed_size)
		self.a_bias= get_var_by_shape(dataset.n_words, )
		self.b_bias= get_var_by_shape(dataset.n_words, )
		self.i2w, self.w2i = dataset.i2w, dataset.w2i
	def fit(self, dataset: GloveDataset, lr=0.05, batch_size=512, n_epochs=3):
		optimizer = Adagrad(self.parameters(), lr=lr)
		dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=8)
		for epoch in trange(n_epochs, desc='epoch'):
			for batch_idx, (L, R, Y) in tqdm(enumerate(dataloader), desc='batch', total=len(dataset) // batch_size):
				loss = self(L.cuda(), R.cuda(), Y.cuda()) # 前向计算得到损失
				optimizer.zero_grad()
				loss.backward()
				optimizer.step()
	def forward(self, L, R, Y):
		W = Y.div(self.y_max).pow(self.alpha).clamp_max(1.0)  # 根据"共现值Y"来确定样本权重, 即公式中的 f(X_{ij})
		pred = torch.einsum('nd,nd->n', self.a_vecs[L], self.b_vecs[R]) + self.a_bias[L] + self.b_bias[R]
		target = (Y + 1).log()  # 注意加一，避免 log(0)溢出
		return W @ mse_loss(pred, target, reduction='none')
	@property
	def embeddings(self):  # 返回中心向量与邻居向量的和; 简单粗暴
		return self.a_vecs + self.b_vecs

GloVe 是如何训练的？

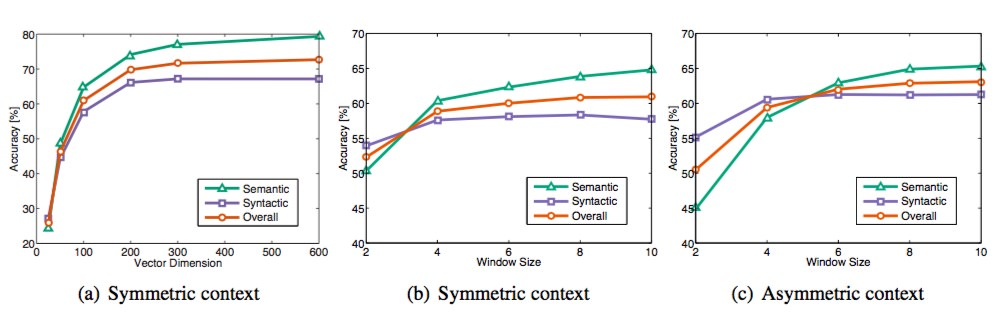
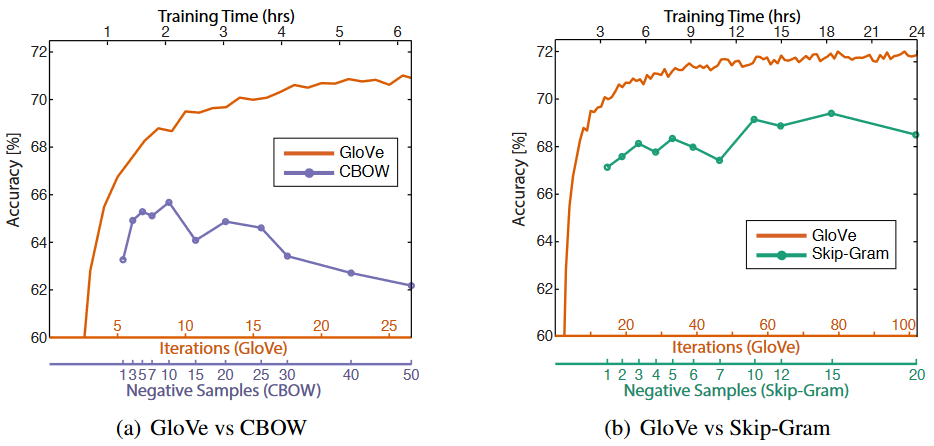
  • 上图是语义准确度，语法准确度以及总体准确度。那么我们不难发现 Vector Dimension 在 300 时能达到最佳，而 context Windows size 大致在 6 到 10 之间
  • 标签问题：GloVe 是无监督的，但是它的标签不像 word 2 vec 一样的 one-hot 标签，而是共现矩阵取对数
  • 词向量：最终学习得到的是两个 vector 是 ww 和 w~\widetilde{w}，因为 X 是对称的（symmetric），所以从原理上讲 ww 和 w~\widetilde{w}是也是对称的，他们唯一的区别是初始化的值不一样，而导致最终的值不一样。所以这两者其实是等价的，都可以当成最终的结果来使用。但是为了提高鲁棒性，我们最终会选择两者之和 ww + w~\widetilde{w}作为最终的 vector

Word2vec 与 glove 的区别？

  • GloVe 与 word2vec，两个模型都可以根据词汇的 “共现 co-occurrence” 信息，将词汇编码成一个向量（所谓共现，即语料中词汇一块出现的频率）
  • word2vec 是局部语料库训练的，其特征提取是基于滑窗的；而 glove 的滑窗是为了构建 co-occurance matrix，是基于全局语料的，可见 glove 需要事先统计共现概率；因此，word2vec 可以进行在线学习，glove 则需要统计固定语料信息
  • word2vec 是无监督学习，同样由于不需要人工标注；glove 通常被认为是无监督学习，但实际上 glove 还是有 label 的，即共现次数 log(Xij)log(X_{ij})
  • word2vec 损失函数实质上是带权重的交叉熵，权重固定；glove 的损失函数是最小平方损失函数，权重可以做映射变换
  • 总体来看，glove 可以被看作是更换了目标函数和权重函数的全局 word2vec，上图是单词类比任务的总体准确度与训练时间的函数关系，可知 GloVe 比 word 2 vec 有更好更快的训练效果

参考：

  1. 简介 GloVe 词向量：推导、实现、应用 - 知乎
  2. 万物皆可 Embedding 之 Word Embedding - 知乎
  3. GloVe 详解 | 永远的热河路
  4. 浅谈：GloVe: Global Vectors for Word Representation - 知乎