图像上采样的方式

发表于 2020-09-09 更新于 2025-01-19 分类于 0-数学基础， G-图形学阅读次数：本文字数： 3.1k 阅读时长 ≈ 3 分钟

图像的插值方式？

在计算机图形学中，插值方法用于在已知数据点之间估计未知数据点的值
1. 最近邻插值（Nearest Neighbor Interpolation）：最简单的插值方法。它找到最接近未知点的已知点，并将该已知点的值分配给未知点。这种方法简单快速，但可能导致图像质量较差，特别是在处理高分辨率图像时
2. 线性插值（Linear Interpolation）：在两个已知点之间假设线性关系。未知点的值是通过在两个已知点之间画一条直线，然后在这条线上找到未知点的位置来计算的。这种方法比最近邻插值更平滑，但可能会在图像中引入一些模糊
3. 双线性插值（Bilinear Interpolation）：是线性插值的二维版本。它在两个方向上进行线性插值，首先在 x 方向上插值，然后在 y 方向上插值。这种方法可以产生比线性插值更平滑的结果，但计算量更大
4. 三次插值（Cubic Interpolation）：在已知点之间假设三次多项式关系。这种方法可以产生非常平滑的结果，但计算量比线性插值和双线性插值更大
5. 三次样条插值（Cubic Spline Interpolation）：是一种更复杂的插值方法，它在每两个点之间使用不同的三次多项式进行插值，同时确保在所有点上的一阶和二阶导数连续。这种方法可以产生非常平滑且无 “振铃” 现象的结果，但计算量比上述所有方法都大
6. 球面插值（Spherical Interpolation，Slerp）：在四维单位球面上进行插值，常用于四元数的插值，特别是在处理旋转时。这种方法可以产生均匀的旋转，但计算量大

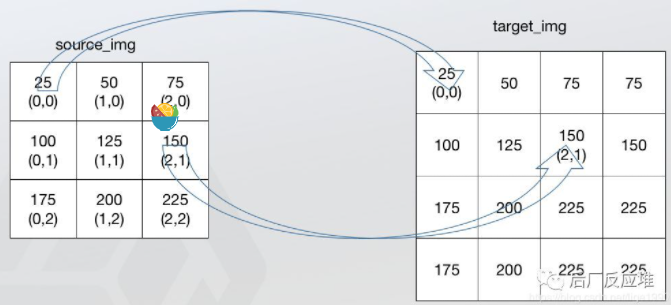
什么是最近邻插值（Nearest Neighbor Interpolation） ?

最近邻插值是最简单的插值方法，选取离目标点最近的点作为新的插入点
OpenCV 使用 cv: : resize 函数可以快速对图像进行最近邻插值插值
1
dst = cv2.resize(image,None,fx=0.5,fy=0.5,interpolation=cv2.INTER_NEAREST)

什么是线性插值（Linear Interpolation）？

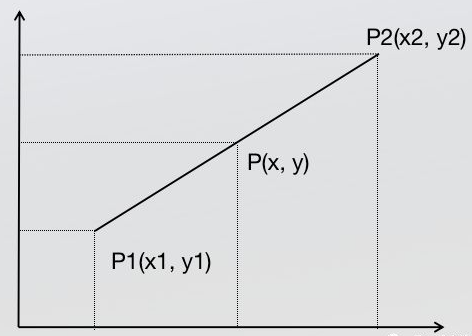
也称单线性插值，指使用连接两个已知量的直线来确定在这两个已知量之间的一个未知量的值的方法
已知中 P 1 点和 P 2 点，坐标分别为 (x 1, y 1)、(x 2, y 2)，要计算 x 1, x 2 区间内某一位置 x 在直线上的 y 值
由三个点在一条线上有，插入位置的 x 值确定，y 可确定

\frac{y-y_{1}}{x-x_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \Rightarrow y=\frac{x_{2}-x}{x_{2}-x_{1}} y_{1}+\frac{x-x_{1}}{x_{2}-x_{1}} y_{2}

什么是双线性插值 (Bilinear Interpolation)?

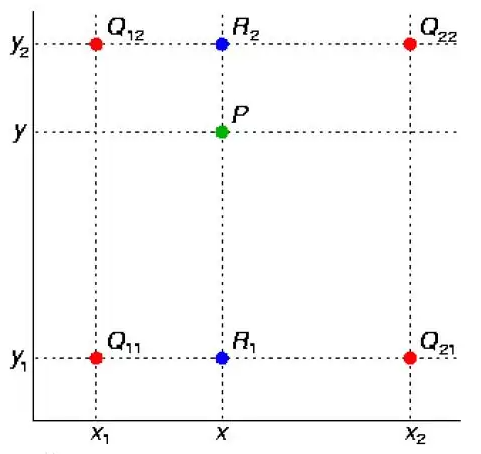
是线性插值的扩展，使用 2×2 相邻像素来获得插值像素的加权平均值进行插值，其核心思想是在两个方向分别进行一次线性插值
假如我们想得到未知函数 _ f_ 在点 _ P_ = (_ x_ , _ y_) 的值，假设我们已知函数 f 在 $Q_{11} = (x_1, y_1), Q_{12} = (x_1, y_2),Q_{21} = (x_2, y_1),Q_{22} = (x_2, y_2)$ 以及四个点的值
x 方向的插值

f\left(R_{1}\right) \approx \frac{x_{2}-x}{x_{2}-x_{1}} f\left(Q_{11}\right)+\frac{x-x_{1}}{x_{2}-x_{1}} f\left(Q_{21}\right) \quad where \quad R_{1}=\left(x, y_{1}\right)\\ f\left(R_{2}\right) \approx \frac{x_{2}-x}{x_{2}-x_{1}} f\left(Q_{12}\right)+\frac{x-x_{1}}{x_{2}-x_{1}} f\left(Q_{22}\right) \quad where \quad R_{2}=\left(x, y_{2}\right)

y 方向的插值

f(P) \approx \frac{y_{2}-y}{y_{2}-y_{1}} f\left(R_{1}\right)+\frac{y-y_{1}}{y_{2}-y_{1}} f\left(R_{2}\right)

OpenCV 使用 cv: : resize 函数可以快速对图像进行双线性插值
1
dst = cv2.resize(image,None,fx=0.5,fy=0.5,interpolation=cv2.INTER_LINEAR)

什么是双三次插值 (Bicubic interpolation)？

使用双三次插值来调整图像大小。在调整新像素的大小和插值时，此方法作用于图像的 4×4 相邻像素。然后，它采用 16 个像素的权重平均值来创建新的插值像素
效果比较好，但是计算代价过大
OpenCV 使用 cv: : resize 函数可以快速对图像进行双三次插值
1
dst = cv2.resize(image,None,fx=0.5,fy=0.5,interpolation=cv2.INTER_CUBIC)

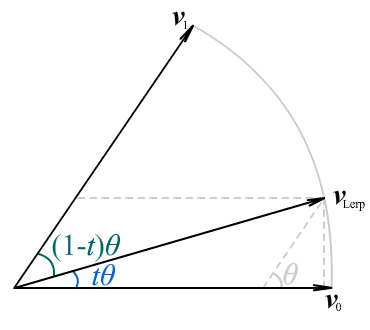
什么是球面插值（Spherical Interpolation，Slerp）？

为了解决插值角速度不匀速，引入了 SLerp，记为 $SLerp(\boldsymbol{v}_0,\boldsymbol{v}_1,t)$ ，t 为插值权重， $\theta$ 是 $v_1,v_2$ 的夹角

SLerp(\boldsymbol{v}_0,\boldsymbol{v}_1,t)=\frac{\sin((1-t)\theta)}{\sin\theta}\boldsymbol{v}_0+\frac{\sin(t\theta)}{\sin\theta}\boldsymbol{v}_1

可以看出 Slerp 是角速度匀速的

参考：

插值算法 —— Lerp, NLerp, SLerp_lerp 算法 - CSDN 博客