信息论

本文讲解了熵的计算过程，并且延伸到交叉熵、KL 散度，这些概念对应神经网络中损失的计算，学习时需要记住熵、交差熵、KL 散度即可

什么是信息量？

• 又称自信息量，表示概率空间中的单一事件或离散随机变量的值相关信息量的量度，如果一件事情的概率很低，那么它的信息量就很大；反之，如果一件事情的概率很高，它的信息量就很低。简而言之，概率小的事件信息量大

  $$H(x)=log{\frac {1} {p(x)}}$$

• 若估计在一次国际象棋比赛中谢军获得冠军的可能性为0.1（记为事件A），而在另一次国际象棋比赛中她得到冠军的可能性为0.9（记为事件B）。试分别计算当你得知她获得该次比赛冠军时，从中获得的信息量各为多少？

  $$\begin{aligned} &\mathrm{H}(\mathrm{A})=-\log _{2} p(0.1) \approx 3.32 \\ &\mathrm{H}(\mathrm{B})=-\log _{2} p(0.9) \approx 0.152 \end{aligned}$$

什么是熵(entropy)？

• 又称经验熵、信息熵，物理上是表示混乱程度、不确定性的度量，在信息论中表示对分信息量期望

  $$H(p)=\sum_{x} p(x)I(x)=\sum_{x} p(x)log(\frac {1} {p(x)})=-\sum_xp(x)log(p(x))$$

• 

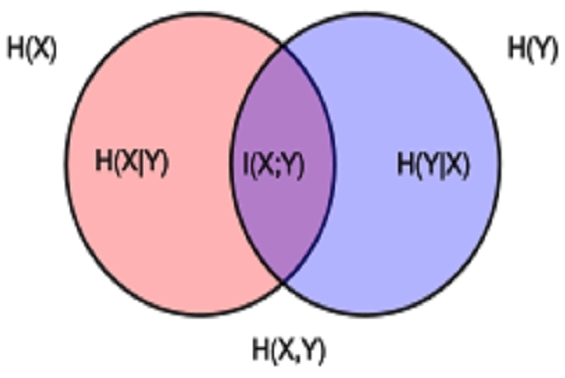
什么是条件熵？

• 又称经验条件熵，表示在已知随机变量X 下随机变量 Y 的不确定，也称给定条件下 Y 的条件概率分布对 X 数学期望，利用 全概率公式计算即可

  $$H(Y|X)=\sum_{x \in X}{p(x)H(Y|X=x)}$$

• 

什么是联合熵？

• 度量一联合概率分布的随机系统的不确定度

  $$H(X,Y)=-\sum_{i=1}^np(x_i,y_i)logp(x_i,y_i)$$

• 
• 

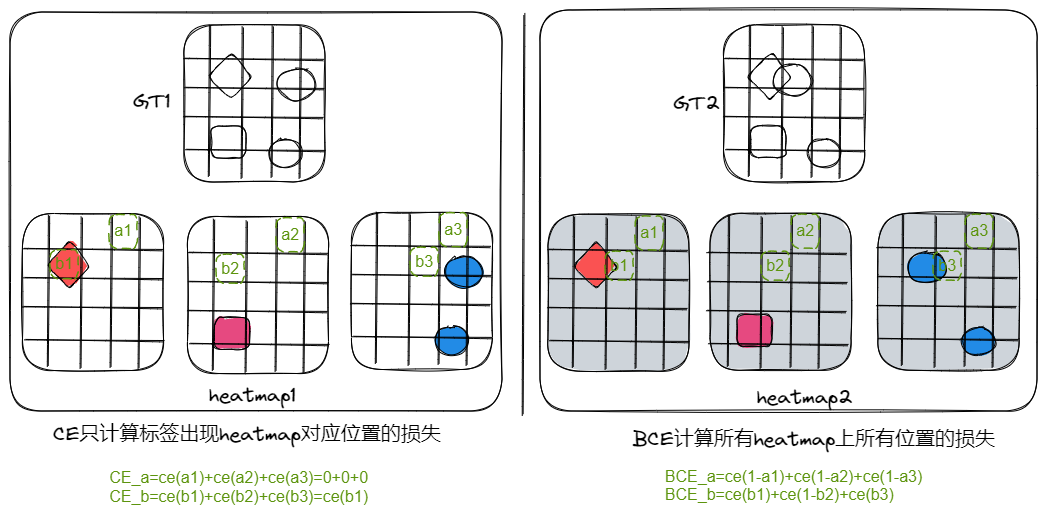
什么是交叉熵损失 (CE Loss) ?

• 
• 表示实际输出（概率）与期望输出（概率）分布的距离，也就是交叉熵的值越小，两个概率分布就越接近
• 二分类 (BCE)：$y_i$ 表示样本 i 的标签，正类为 1，负类为 0；$p_i$ 为样本 i 为正类的概率

  $$L=\frac{1}{N} \sum_{i} L_{i}=\frac{1}{N} \sum_{i}-\left[y_{i} \cdot \log \left(p_{i}\right)+\left(1-y_{i}\right) \cdot \log \left(1-p_{i}\right)\right]$$

• 多分类 (CE)：$M$ 为类别数量；$y_i$ 表示样本 i 的标签， $p_{ic}$ 为样本 i 为 c 的概率

  $$L=\frac{1}{N} \sum_{i} L_{i}=-\frac{1}{N} \sum_{i} \sum_{c=1}^{M} y_{i c} \log \left(p_{i c}\right)$$

• 在区分前景、背景的二分类时，当前景像素的数量远远小于背景像素的数量时，y=0 的数量远大于 y=1 的数量，损失函数 y=0 的成分就会占据主导，使得模型严重偏向背景，导致效果不好
• 在多分类任务中，交叉熵擅长于学习类间的信息，因为它采用了类间竞争机制，它只关心对于正确标签预测概率的准确性，忽略了其他非正确标签的差异，导致学习到的特征比较散

  >>> dummy_input=torch.rand([1,10,3,3])
  >>> dummy_target = torch.randint(0,11,[1,3,3]) #为每个位置生成一个gt标签                                                                    
  >>> dummy_input.shape,dummy_target.shape
  (torch.Size([1, 10, 3, 3]), torch.Size([1, 3, 3]))
  >>> dummy_target
  tensor([[[ 8,  9,  1],  
          [ 4,  0,  6],  
          [10,  0,  1]]])
  >>> certerion = torch.nn.CrossEntropyLoss(reduction='none',ignore_index=10)
  >>> certerion(dummy_input,dummy_target) # 忽略类别损失为0
  tensor([[[1.9907, 2.7757, 2.2835],
          [2.7387, 2.1581, 2.3648],
          [0.0000, 2.4749, 2.0570]]])

什么是二值交叉熵损失 (BCELoss)？

• 
• 二值交叉熵损失 (Binary Cross Entropy Loss，BCELoss)，用于二分类，不能进行多分类，但是可进行多标签分类（一个样本对应多个标签）
• BCEWithLogitsLoss 将 sigmoid 和二值交叉熵损失 BCELoss 合并为一步，以下 3 种方式计算结果相同

  >>> dummy_input=torch.rand([1,10,3,3])
  >>> dummy_target = torch.randint(0,10,[1,10,3,3],dtype=torch.float32) #为每个位置生成多个gt标签 
  >>> dummy_input.shape,dummy_target.shape # shape必须一致
  (torch.Size([1, 10, 3, 3]), torch.Size([1, 10, 3, 3]))   
  >>> crition1 = torch.nn.BCEWithLogitsLoss()
  >>> crition1(dummy_input,dummy_target)      
  tensor(-1.2125)
  >>> crition2 = torch.nn.MultiLabelSoftMarginLoss()
  >>> crition2(dummy_input,dummy_target)
  tensor(-1.2125)
  >>> crition3 = torch.nn.BCELoss()
  >>> crition3(torch.sigmoid(dummy_input), dummy_target) 
  tensor(-1.2125)

什么是 KL 散度损失 (KLDivLoss)？

• KL 散度衡量两个连续分布之间的距离。两个分布越相似，KL 散度越接近 0，KL 散度又称相对熵

  $$\operatorname{los} s(x, y)=\frac{1}{n} \Sigma_{i}\left(x_{i} \times \log \frac{x_{i}}{y_{i}}\right)$$

• 注意，使用 nn. KLDivLoss 计算 KL (pred|target)时，需要将 pred 和 target 调换位置，而且 target 需要先取对数
• 在机器学习的分类问题中，我们希望缩小模型预测和标签之间的差距，即 KL 散度越小越好，在这里由于 KL 散度中的 H (p)项不变（在其他问题中未必），故在优化过程中只需要关注交叉熵就可以了，因此一般使用交叉熵作为损失函数

什么是信息增益？

• 
• 表示得知特征 X 的信息时，使得类 Y 的信息不确定性减少的程度，定义为 Y 熵 (entropy) H (Y)与特征 A 经条件熵 H (Y|A)之差 ID 3 决策树使用该指标构建

  $$g(X,Y)=H(Y)-H(Y|X)$$

什么是信息增益率？

• 
• 信息增益的进一步优化，解决信息增益偏向取值较多的特征的问题 C 4.5 决策树使用该指标构建决策树

  $$\begin{array}{l}g_R(X,Y)=\frac {g(X,Y)} {H_X(Y)}\\ H_X(Y)=-\sum_{i=1}^n \frac {X_i} {X}log_2\frac {X_i} {X}\end{array}$$

什么是基尼系数 (Gini)？

• 表示在样本集合中一个随机选中的样本被分错的概率，越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。决策树算 CART 使用

  $$Gini(X)=\sum_{x \in X}p(x)(1-p(x))=1-\sum_{x \in X}p(x)^2$$

• 基尼系数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率
• 基尼系数值越大，样本集合的不确定性也就越大，这一点与熵相似

什么是 KL 散度？

• 又称相对熵、信息散度、信息增益，衡量两个概率分布 P 和 Q 的差异。在经典境况下，P 表示数据的真实分布，Q 表示数据的理论分布，模型分布。差异越大则 KL 散度越大，差异越小则 KL 散度越小

  $$D(P|Q)=\sum P(x)log \frac {P(x)} {Q(x)}$$

• 已知随机变量 X∼P 取值为 1, 2, 3 时的概率分别 [0.2, 0.4, 0.4]，随机变量 Y∼Q 取值为 1, 2, 3 时的概率分别 [0.4, 0.2, 0.4]

  $$D(P|Q)=0.2*log\frac{0.2}{0.4}+0.4*log\frac{0.4}{0.2}+0.4*log\frac{0.4}{0.4}=0.138$$

什么是 JS 散度？

• 度量了两个概率分布的相似度，基 KL 散度的变体，解决了 KL 散度非对称的问题

  $$JS(P||Q)=\frac {1}{2}KL(P(x)||\frac{P(x)+Q(x)}{2}+\frac {1}{2}KL(Q(x)||\frac{P(x)+Q(x)}{2})$$

信息熵、交叉熵、KL 散度的区别？

• 关于样本集的两个概率分布 p 和 q，设 p 为真实的分布，比如[1, 0, 0]表示当前样本属于第一类，q 为拟合的分布，比如[0.7, 0.2, 0.1]
• 按照真实分布 p 来衡量识别一个样本所需的编码长度的期望，即平均编码长度（信息熵）

  $$H(p)=-\sum_{i=1}^C p(x_i)log(p(x_i))$$

• 如果使用拟合分布 q 来表示来自真实分布 p 的编码长度的期望，即平均编码长度（交叉熵）

  $$H(p,q)=-\sum_{i=1}^{C}p(x_i)log(q(x_i))$$

• 观上，用 p 来描述样本是最完美的，用 q 描述样本就不那么完美，根据吉布斯不等式，$H(p,q)\geq H(p)$ 恒成立，当 q 为真实分布时取等，我们将由 q 得到的平均编码长度比由 p 得到的平均编码长度多出的 bit 数称为相对熵，也叫 KL 散度。KL 散度 = 交叉熵 - 信息熵

  $$\begin{aligned}&\mathrm{D_{KL}\left(p||q\right)=\sum_{i=1}^{n}p(x_i)\log\left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right)} \\&=\sum_{i=1}^np(x_i)log(p(x_i))-\sum_{i=1}^np(x_i)log(q(x_i)) \\&=-H(p)+H(p,q)\end{aligned}$$

• 在机器学习的分类问题中，我们希望缩小模型预测和标签之间的差距，即 KL 散度越小越好，在这里由于 KL 散度中的 H (p)项不变（在其他问题中未必），故在优化过程中只需要关注交叉熵就可以了，因此一般使用交叉熵作为损失函数

参考：

1. PyTorch学习笔记——多分类交叉熵损失函数 - 知乎
2. 交叉熵损失函数原理详解_Cigar丶的博客-CSDN博客