ILVR：Conditioning Method for Denoising Diffusion Probabilistic Models

发表于 更新于 分类于 ， ， ， 阅读次数： 本文字数： 3.2k 阅读时长 ≈ 3 分钟

无需显式训练，只需要在测试时通过分析去躁过程生成图片和条件图片的低级特征，引导生成图片过程
(图片)-> 噪声 + 条件（图片）-> 条件图片，条件图片

什么是 ILVR ？

  • 通过精调 DDPM 逆向过程的每一步，让生成的图像 x0x_0 接近参考图像。所谓接近，即作者希望 DDPM 能够满

ϕN(xt)=ϕN(yt)\phi_{N}(\mathbf{x}_{t})=\phi_{N}(\mathbf{y}_{t})

  • 以上过程在无需额外模型或学习过程，因为 ϕN\phi_{N} 是一个无参的上下采样方法，N 指上下采样的倍率
  • ILVR 可以有许多有趣的应用，比如给一个在狗上面训练的模型以猫作为参考图像，并合理控制 N，那么模型就会生成像这只猫的狗

ILVR 的原理？

  • 1）我们的目标是从条件分布里完成抽样，即 pθ(x0∣c)p_{\theta}(x_{0}|c)，那么根据马尔可夫链的性质，可以展开成如下：

pθ(x0∣c)=∫pθ(x0:T∣c)dx1:T,pθ(x0:T∣c)=pθ(xT)∏t=1Tpθ(xt−1∣xt,c)\begin{gathered}p_\theta(x_0|c)=\int p_\theta(x_{0:T}|c)dx_{1:T},\\p_\theta(x_{0:T}|c)=p_\theta(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t,c)\end{gathered}

  • 2）令 ϕN(⋅)\phi_{N}(\cdot) 代表一个线性的低通滤波操作，一系列的上下采样，缩放因子为 N，给定一个参考图片 y，那么其对应的条件就是，确保 ϕN(x0)=ϕN(y)\phi_{N}(x_{0})=\phi_{N}(y)。其物理意义是想要生成的样本和 reference image 共享语义信息，语义信息具体层次由缩放因子决

pθ(xt−1∣xt,c)=pθ(xt−1∣xt,ϕN(x0)=ϕN(y))≈pθ(xt−1∣xt,ϕN(xt−1)=ϕN(yt−1))\begin{aligned}p_\theta(x_{t-1}|x_t,c)&=p_\theta(x_{t-1}|x_t,\phi_N(x_0)=\phi_N(y))\\&\approx p_\theta(x_{t-1}|x_t,\phi_N(x_{t-1})=\phi_N(y_{t-1}))\end{aligned}

  • 3）其中 yty_t 是根据 前向扩散 的公式算得，在每个转移中的条件 c 可以被替换成一个 local 形式，即隐变量 xt−1x_{t-1} 和参考变量 yt−1y_{t-1} 共享低频内

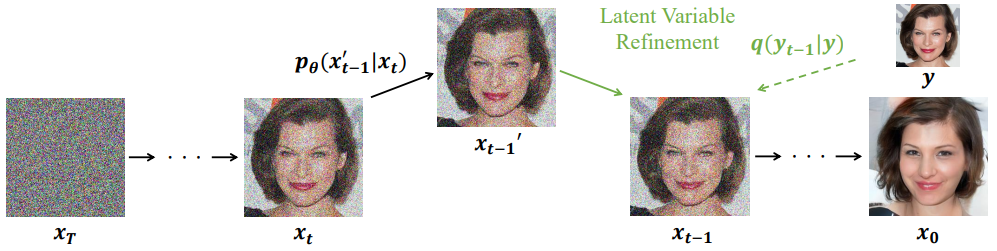
xt−1′∼pθ(xt−1′∣xt),xt−1=ϕ(yt−1)+(I−ϕ)(xt−1′)\begin{aligned}x_{t-1}^{\prime}&\sim p_\theta(x_{t-1}^{\prime}|x_t),\\x_{t-1}&=\phi(y_{t-1})+(I-\phi)(x_{t-1}^{\prime})\end{aligned}

ILVR 的低通滤波操作？

  • 是一系列的上下采样，缩放因子为 N，可以使用双线性插值、双三次插值实现，原文继承 torch. Nn. Moudule 实现了一个无参的上下采样过程
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    for i in num_timesteps:
    	t = th.tensor([i] * shape[0], device=device)
    	with th.no_grad():
    		# Xt->Xt-1，去躁过程
    		denoise_img = self.p_sample(model,img,t)
    		#### ILVR ####
    		if i > range_t:
    			# Y->Yt-1，示例图片的加躁过程
    			ref_img_noise=self.q_sample(ref_img, t, th.randn(*shape))
    			# Xt-1=Xt+Q(Yt-1)-Q(Xt-1)
    			denoise_img = img  + up(down(ref_img_noise))- up(down(denoise_img))
    	img = denoise_img

ILVR 的低通滤波操作 N 对结果的影响？

  • 下采样率 N 是一个超参数， N 越小，保留细节越多，生成图像就越接近参考图像。作者还指出，我们不一定在整个逆向过程都用到参考图像，可以只选择某些步用。选的步数越多，留给随机采样的发挥空间就越少，生成图像也越接近参考图像

ILVR 与 classifier guidance 的联系？

  • ILVR 和 classifier guidance 的本质是一样的。ILVR：对采样的结果偏移了 ϕN(yt−1)−ϕN(xt−1′)\phi_{N}(\mathbf{y}_{t-1})-\phi_{N}(\mathbf{x}_{t-1}^{\prime})；Classifier guidance：对采样分布的均值偏移了 sΣ∇xlog⁡p(y∣x)∣x=μs\Sigma\nabla_{\mathbf{x}}\log p(y|\mathbf{x})|_{\mathbf{x}=\mu}
  • 一方面，偏移结果（先采样再偏移）和偏移均值（先偏移再采样）显然是等价的；另一方面 ϕN(yt−1)−ϕN(xt−1′)\phi_{N}(\mathbf{y}_{t-1})-\phi_{N}(\mathbf{x}_{t-1}^{\prime}) 大致是 xt−1′x_{t-1}^{'} 到 yt−1y_{t-1} 方向的向量，朝该方向走能够提升 p(yt−1∣xt−1)p(y_{t-1}|x_{t-1})，这与 ∇xlog⁡p(yt−1∣xt−1)\nabla_{\mathbf{x}}\log p(\mathbf{y}_{t-1}|\mathbf{x}_{t-1}) 的意义相吻合
  • 更有甚者，二者都有一个控制引导强度的超参数：下采样率 N 和 guidance scale s，当 N 增大时，满足 ϕN(xt)=ϕN(yt)\phi_{N}(\mathbf{x}_{t})=\phi_{N}(\mathbf{y}_{t}) 的 yty_t 更多，相当于 p(yt−1∣xt−1)p(y_{t-1}|x_{t-1}) 分布变得更平缓，引导作用更弱；而 s 减小时，p(y∣x)sp(y|x)^s 也是变得更平缓，引导作用也是更弱
  • 后文的许多工作都可以与 classifier guidance 建立起类似的联系。这类方法的特点是无需训练，只需要加载预训练模型，对逆向采样过程施加引导即可，对算力要求十分友好

参考：

  1. ILVR: Conditioning Method for Denoising Diffusion Probabilistic Models - 知乎
  2. 扩散模型应用・图生图与图像恢复 - 知乎