STLNet

STLNet 在底层网络中利用和增强图片的纹理信息（全局），而不是直接跨连接利用局部信息，得到更加优秀的性能

什么是 STLNet ？

• 
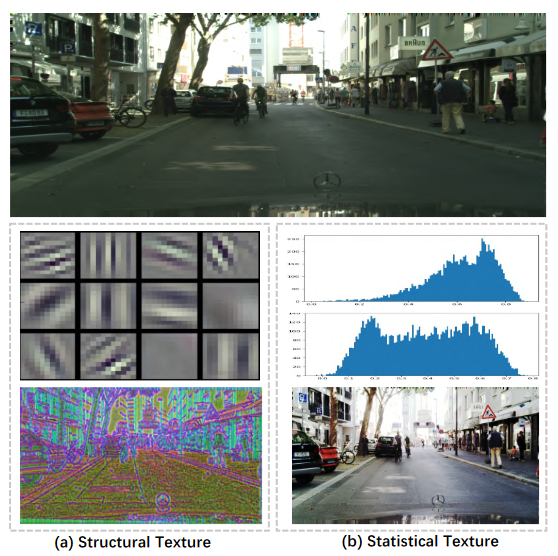
• 目前语义分割大部分工作集中在学习卷积网络的高级语义特征或者上下文信息，对于低级特征一般会考虑通过桥接与更深层次的特征信息直接融合。这样的处理比较粗糙，本文提出一种学习低层特征里的统计纹理的方法，通过提取和增强纹理信息，使模型达到优秀性能

STLNet 的网络结构？

• 
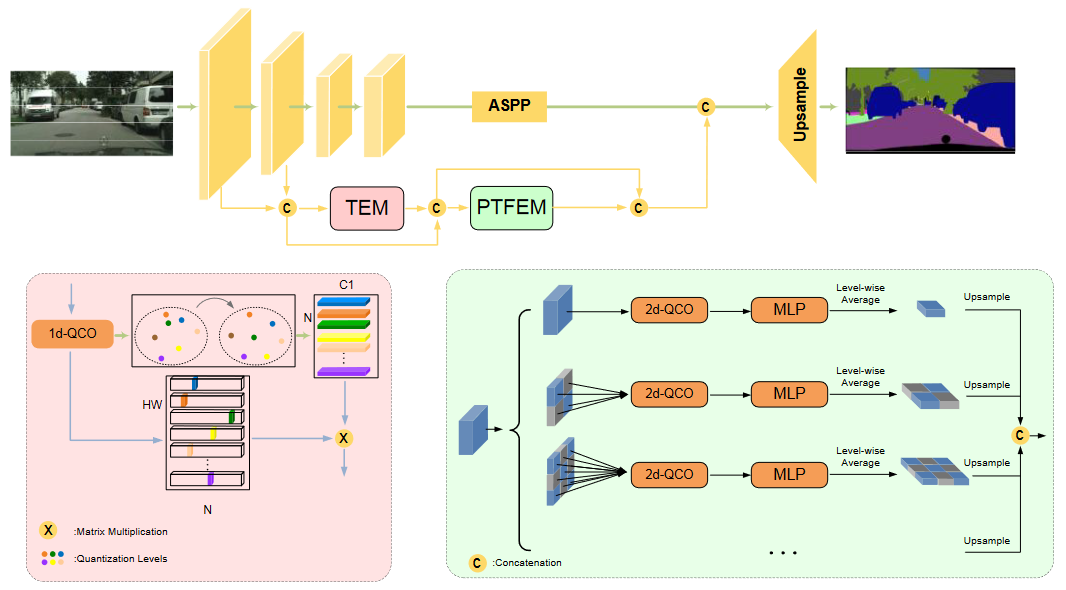
• 和 [[DeepLabv3]] 的结构很像，除了增加下分支用于学习图片的纹理信息

STLNet 的纹理增强模块 (TEM)？

• 
• 1-d QCO 提供了一种统计化纹理表征的方式，TEM 是受到传统图像处理方法中直方图均衡化的启发。 该算法旨在对每个灰度级进行重建，且在对某个级数进行重建的过程中需要感知其他级数的统计信息。这可以看作是一个 graph。因此，我们将其扩展到一个可学习的 graph 来对每个量化级进行重建。在这个 graph 中，节点是 D 中所包含的每个量化级的统计信息。该 graph 的实现方式是一个非常常规的 graph reasoning

STLNet 的金字塔纹理特征提取模块 (PTEEM)?

• 
• 类似于 pspnet，在 ResNet 的 layer3 之后添加了一个辅助层，得到一个辅助预测图。两个预测图对应两个 loss 值，加权求和

STLNet 的 1-d QCO 模块？

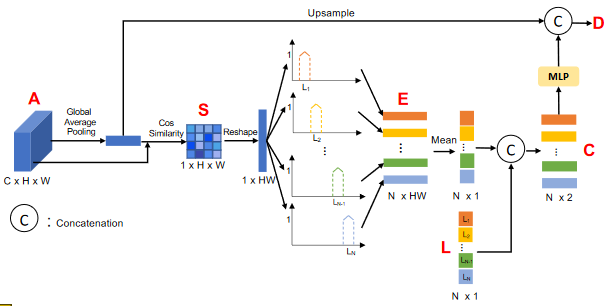
• QCO (Quantization and Counting Operator) 包含量化 (A-L)、统计 (L+S->E)、平均编码 (E’+L->C) 3 个操作，类似灰度直方图，只针对单个位置上的量化，统计也是 1 维上的统计
• A->S：输入 A ($C\times H\times W$) 经过 GAP 后，得到 g ($C\times 1\times 1$)，然后 A 每个位置长度为 $C\times 1\times 1$ 的特征按照以下公式算余弦相似度矩阵 S ($1\times H\times W$)$$\mathbf{S}{i,j}=\frac{g\cdot\mathbf{A}{i,j}}{|g|2\cdot|\mathbf{A}{i,j}|_2}$$
• S->L：对余弦相似度矩阵 S 进行量化统计，以提取类似于直方图的信息表征。首先对余弦相似度矩阵 S 进行量化分级，均分为 N 个量化级，得到 L ($N\times 1$)，第 n 个量化级按照以下公式计算 $$\mathbf {L}_{n}=\dfrac {max\left (\mathbf {S}\right)-min\left (\mathbf {S}\right)}{N}\cdot n+min (\mathbf {S})$$
• L+S->E：基于得到的 L，对 S 进行量化编码，即每个像素的 $S_i$ 被 N 个函数 $L_0...L_n$ 编码成一个 N 维向量 E，编码方式如下：$$\mathbf {E}_{i,n}=\begin {cases} 1-|\mathbf {L}_n-\mathbf {S}_i|&if&-\frac {0.5}{N}\leq\mathbf {L}_n-\mathbf {S}_i<\frac {0.5}{N}\ 0&else\end {cases}$$
• E’+L->C：首先对 E 按照 i 方向求平均值，表示 N 个函数对 S 的平均编码，这一步得到 E’（$N\times 1$）, E’与 Lconcate 得到 C（$N\times 2$）
• C->D: C（$N\times 2$）经过 MLP 得到 $N\times C1$ 的特征，与 g 的上采样特征 $N\times C$ 融合后，得到 D ($N\times (C+C1)$ )

STLNet 的 2-d QCO 模块？

• 
• 二维量化，针对的是相邻两个位置（ 比较和 $E_{i,j}$ 和 $E_{i,j+1}$ 的这两个一维的量化，生成二维量化，$0\leq i\leq H,0\leq j\leq W$
• 同 1-d QCO 类似，全局池化，计算相对于平均特征的余弦相似度，N 个等级的量化，得到相同意义上的 E 和 L
• 接下来 $E_{i,j}$ 和 $E_{i,j+1}$ 这种相邻位置的量化矩阵通过转置相乘，得到一个 NxN 的二维矩阵 $\hat E$，类似于 E，它也是一个十分稀疏的矩阵，大部分地方都是 0，它表示每两个相邻像素的量化相关性
• 接下来是统计，就像 1-d QCO 结构中，从 E 得到 C 的过程一样。2-d QCO 从 $\hat E$ 得到的 C 仍然是一个二维 tensor，表示的是每个 (Lm, Ln) 的出现数的归一化值。只不过 1-d 中是 N，2-d 中是 NxN，对于 g，先利用上采样，从 1xC 变成 NxNxC 的 tensor

参考：
Learning Statistical Texture for Semantic Segmentation - 知乎