K-Means

发表于 更新于 分类于 ， 阅读次数： 本文字数： 2k 阅读时长 ≈ 2 分钟

本文讲解 kmeans 的原理，着重理解影响 kmeans 结果的 3 个因素及 K 值的确定办法

什么是 K-means 算法？

  • 通过尝试将样本分成 n 个方差相等的组来对数据进行聚类，最小化称为惯性或聚类内平方和的标
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
     >>> from sklearn.cluster import KMeans
     >>> import numpy as np
     >>> X = np.array([[1, 2], [1, 4], [1, 0],
    ...               [10, 2], [10, 4], [10, 0]])
     >>> kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
     >>> kmeans.labels_
    array([1, 1, 1, 0, 0, 0], dtype=int32)
     >>> kmeans.predict([[0, 0], [12, 3]])
    array([1, 0], dtype=int32)
     >>> kmeans.cluster_centers_
    array([[10.,  2.],
    	   [ 1.,  2.]])

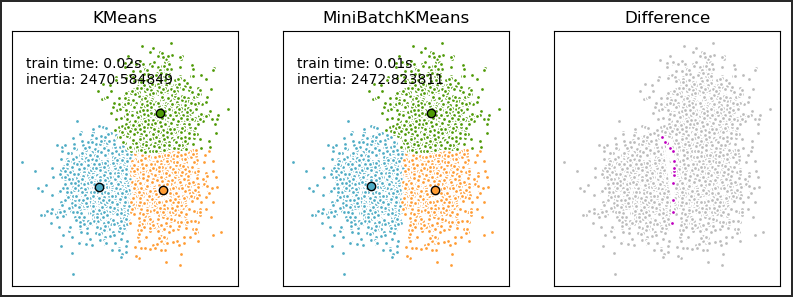
什么是小批量的 K-means 算法？

  • MiniBatchKMeans 是该 KMeans 算法的一种变体，它使用小批量来减少计算时间，同时仍然尝试优化相同的目标函数。小批量是输入数据的子集，在每次训练迭代中随机采样。这些小批量大大减少了收敛到本地解决方案所需的计算量
  • MiniBatchKMeans 收敛速度比 快 KMeans，但结果的质量会降低。在实践中，这种质量差异可能非常小

影响基本 K - 均值算法的主要因素？

  • 样本输入顺序
  • 模式相似性测度
  • 初始类中心的选取

如何选择 kmeans 中的 K 值？

  • 有两个方法，手肘法及轮廓系数法
  • 手肘法：核心指标是 SSE (sum of the squared errors，误差平方和)，其中，Ci 是第 i 个簇，p 是 Ci 中的样本点，mi 是 Ci 的质心（Ci 中所有样本的均值），SSE 是所有样本的聚类误差，代表了聚类效果的好坏。随着聚类数 k 的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和 SSE 自然会逐渐变小；当 k 小于真实聚类数时，由于 k 的增大会大幅增加每个簇的聚合程度，故 SSE 的下降幅度会很大；当 k 到达真实聚类数时，再增加 k 所得到的聚合程度回报会迅速变小，所以 SSE 的下降幅度会骤减，然后随着 k 值的继续增大而趋于平缓，也就是说 SSE 和 k 的关系图是一个手肘的形状，而这个肘部对应的 k 值就是数据的真实聚类数

SSE=∑i=1k∑p∈Ci∣p−mi∣2SSE=\sum_{i=1}^k\sum_{p \in C_i}|p-m_i|^2

  • 轮廓系数法：核心指标是轮廓系数，a 是 Xi 与同簇的其他样本的平均距离，称为凝聚度，b 是 Xi 与最近簇中所有样本的平均距离，称为分离度。平均轮廓系数的取值范围为 [-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。那么，很自然地，平均轮廓系数最大的 k 便是最佳聚类数

S=b−amax(a−b)S=\frac{b-a}{max(a-b)}

在 k-means 或 kNN，我们是用欧氏距离 (L2 距离) 来计算最近的邻居之间的距离。为什么不用曼哈顿距离？

  • 曼哈顿距离只计算水平或垂直距离，有维度的限制。
  • 欧氏距离 (L2 距离) 可用于任何空间的距离计算问题。因为，数据点可以存在于任何空间，欧氏距离是更可行的选择。例如：想象一下国际象棋棋盘，象或车所做的移动是由曼哈顿距离计算的，因为它们是在各自的水平和垂直方向做的运动

优化 Kmeans？

  • 使用 Kd 树或者 Ball Tree 将所有的观测实例构建成一颗 kd 树，之前每个聚类中心都是需要和每个观测点做依次距离计算，现在这些聚类中心根据 kd 树只需要计算附近的一个局部区域即可

Kmeans 的复杂度？

  • 时间复杂度：O (tKmn)，其中，t 为迭代次数，K 为簇的数目，m 为记录数，n 为维数
  • 空间复杂度：O ((m+K) n)，其中，K 为簇的数目，m 为记录数，n 为维数

KMeans 初始类簇中心点的选取？

  • 从输入的数据点集合中随机选择一个点作为第一个聚类中心
  • 对于数据集中的每一个点 x，计算它与最近聚类中心 (指已选择的聚类中心) 的距离 D (x)
  • 选择一个新的数据点作为新的聚类中心，选择的原则是：D (x) 较大的点，被选取作为聚类中心的概率较大
  • 重复 2 和 3 直到 k 个聚类中心被选出来
  • 利用这 k 个初始的聚类中心来运行标准的 k-means 算法

什么是 k-median?

  • 与 k-means 紧密相关的聚类算法。两者的实际区别如下： 对于 k-means，确定形心的方法是，最大限度地减小候选形心与它的每个样本之间的距离平方和
  • 对于 k-median，确定形心的方法是，最大限度地减小候选形心与它的每个样本之间的距离总和。