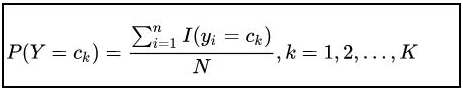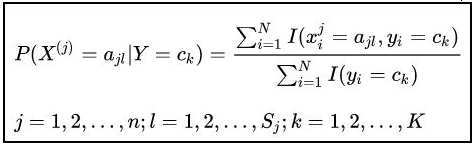朴素贝叶斯 - NBC
根据贝叶斯定理开发的分类方法,贝叶斯定理是通过先验概率求解后验概率的过程,是一个通过试验不断修正后验概率的过程
什么是朴素贝叶斯法?
- 朴素贝叶斯法是基于贝叶斯定理与特征独立事件的 ** 分类方法,已知贝叶斯定理如下:
- 应用到分类时,只需要假设 A 是类别,B 是特征,于是公式简化如下,又因为分母对任意类别来说都是一样的,所以只需要比较分子的大小,就可判定特定特征下属于某类别的概率,即完成分类:
- 例子
![]()
为什么朴素贝叶斯如此 “朴素”?
- 因为它假定所有的特征在数据集中的作用是同样重要和独立的。正如我们所知,这个假设在现实世界中是很不真实的,因此,说朴素贝叶斯真的很 “朴素”
朴素贝叶斯法的贝叶斯估计?
- 为什么要使用贝叶斯估计:用极大似然估计 (MLE) 可能会出现所要估计的概率值为 0 的情况(如没有出现的类别,先验概率为 0)。这时会影响到后验概率的计算结果,使分类产生偏差
- 先验概率的贝叶斯估计(k 为 Y 可能的取值个数)
- 条件概率的贝叶斯估计(Sj 为特征 X (j) 可能取值个数)
朴素贝叶斯法的模型表示?
朴素贝叶斯法的模型学习过程?
朴素贝叶斯法的极大似然估计?
朴素贝叶斯缺点?
- 在属性个数比较多或者属性之间相关性较大时,NBC 模型的分类效果相对较差
- 算法是基于条件独立性假设的,在实际应用中很难成立,故会影响分类效果
朴素贝叶斯优点?
- NBC 算法逻辑简单,易于实现
- NBC 算法所需估计的参数很少
- NBC 算法对缺失数据不太敏感
- NBC 算法具有较小的误差分类率
- NBC 算法性能稳定,健壮性比较好
什么是高斯朴素贝叶斯 (Gaussian Naive Bayes)?
- GaussianNB 实现了用于分类的高斯 Naive Bayes 算法。假设特征的可能性是高斯的
1
2
3
4
5
6
7
8
9
10
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.naive_bayes import GaussianNB
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
>>> gnb = GaussianNB()
>>> y_pred = gnb.fit(X_train, y_train).predict(X_test)
>>> print("Number of mislabeled points out of a total %d points : %d"
... % (X_test.shape[0], (y_test != y_pred).sum()))
Number of mislabeled points out of a total 75 points : 4
什么是多项式朴素贝叶斯 (Multinomial Naive Bayes) ?
- 实现了多指标分布数据的朴素贝叶斯算法,是文本分类中使用的两个经典的朴素贝叶斯变体之一(其中数据通常表示为词向量计数,尽管 tf-idf 向量在实践中也被认为效果很好)
1
2
3
4
5
6
7
8
9
10>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.fit(X, y)
MultinomialNB()
>>> print(clf.predict(X[2:3]))
[3]
什么是补充朴素贝叶斯 (Complement Naive Bayes) ?
- 实现了补充朴素贝叶斯(CNB)算法。CNB 是对标准的多叉朴素贝叶斯(NBB)算法的改编,特别适用于不平衡的数据集。具体来说,CNB 使用每个类的补数的统计数据来计算模型的权重。CNB 的发明者根据经验表明,CNB 的参数估计比 MNB 的参数估计更稳定。此外,CNB 在文本分类任务上经常优于 MNB(通常有相当大的差距)
1
2
3
4
5
6
7
8
9
10>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import ComplementNB
>>> clf = ComplementNB()
>>> clf.fit(X, y)
ComplementNB()
>>> print(clf.predict(X[2:3]))
[3]
什么是伯努利朴素贝叶斯 (Bernoulli Naive Bayes) ?
- 根据多变量 Bernoulli 分布的数据实现天真贝叶斯训练和分类算法;即,可能有多个特征,但每个特征都被假定为二进制值(Bernoulli,布尔)变量。因此,该类要求样本被表示为二值特征向量;如果交给任何其他类型的数据,BernoulliNB 实例可以对其输入进行二值化
1
2
3
4
5
6
7
8
9
10>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> Y = np.array([1, 2, 3, 4, 4, 5])
>>> from sklearn.naive_bayes import BernoulliNB
>>> clf = BernoulliNB()
>>> clf.fit(X, Y)
BernoulliNB()
>>> print(clf.predict(X[2:3]))
[3]
什么是分类朴素贝叶斯 (Categorical Naive Bayes) ?
- 实现了分类分布数据的分类朴素贝叶斯算法。它假定由索引 i 描述的每个特征都有自己的分类分布
1
2
3
4
5
6
7
8
9
10>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import CategoricalNB
>>> clf = CategoricalNB()
>>> clf.fit(X, y)
CategoricalNB()
>>> print(clf.predict(X[2:3]))
[3]
什么是核外朴素贝叶斯 (Out-of-core Naive Bayes) ?
- 用来解决大规模的分类问题,对于这些问题,完整的训练集可能不适合放在内存中。为了处理这种情况,MultinomialNB、BernoulliNB 和 GaussianNB 提供了一种部分拟合方法,可以像其他分类器那样逐步使用
参考: