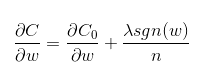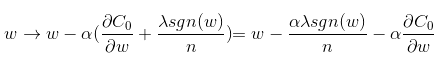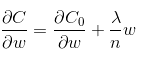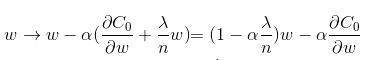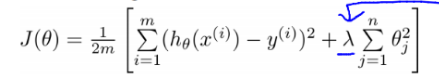机器学习的正则化方法

发表于 更新于 分类于 阅读次数： 本文字数： 2.1k 阅读时长 ≈ 2 分钟

在搭建机器学习模型时，除了对目标计算损失外，还可对参数加入约束，以使得模型泛化能力更强

什么是正则化 (regularization)？

  • 正则化是针过拟合 (overfitting) 而提出的，在求解模型最优一般是优经验风险最小化，在该经验风险上加入模型复杂度结构风险最小化)，从而避免过拟合的危险
  • 常见的正则化 L1 正则化、L2 正则化、丢弃正则化 (Dropout) ，其中 L1 正则化倾向稀疏权重 (减少参数)、L2 正则倾向缩小权重 (减小参数)、Dropout 倾向减小神经元之间共适应性，相当于在原来模型基础上加入先验信息，也就是说，正则化可以在学习过程中降低模型复杂度和不稳定程度

什么是 L1 正则化？

  • 一种正则化，根据权重的绝对值的总和来惩罚权重。在依赖稀疏特征的模型中，L1 正则化有助于使不相关或几乎不相关的特征的权重正好为 0（减少参数），从而将这些特征从模型中移除。与 L2 正则化相

L=Ein+λ∑j∣wj∣L=E_{in}+\lambda\sum_j|w_j|

什么是 L2 正则化？

  • 一种正则化，根据权重的平方和来惩罚权重。L2 正则化有助于使离群值（具有较大正值或较小负值）权重接近于 0（减少参数），但又不正好为 0。（与 L1 正则化相对。）在线性模型中，L2 正则化始终可以改进泛

L=Ein+λ∑jwj2L=E_{in}+\lambda\sum_jw_j^2

什么是 Tikhonov (吉洪诺夫) 正则化？

  • 适定性问题常见的正则化方法 ，在统计学上，这种方法被称 Ridge 回归 (岭回归)，在机器学习中，它被称什么是权重衰减 (weight decay)?
  • 对于y=Xm,nwy=X_{m,n}w ，当m>nm>n 时，利用最小二乘法求解 w 时， 会出现发散或对 w 的不合理逼近，为解决这个问题，吉洪诺夫提出了利用正则化项修普通最小二乘法 (OLS) 的代价函

min⁡w∣∣Xw−y∣∣22+α∣∣w∣∣22\min_{w} || X w - y||_2^2 + \alpha ||w||_2^2

L1 和 L2 正则先验分别服从什么分布？

  • 对参数引拉普拉斯分布等价 L1 正则化
  • 对参数引高斯正态分布 (normal) 相当 L2 正则化
  • 正则化参数等价于对参数引入先验分布，使得 模型复杂度 变小（缩小解空间），对于噪声以及异常值的鲁棒性增强泛化能力）

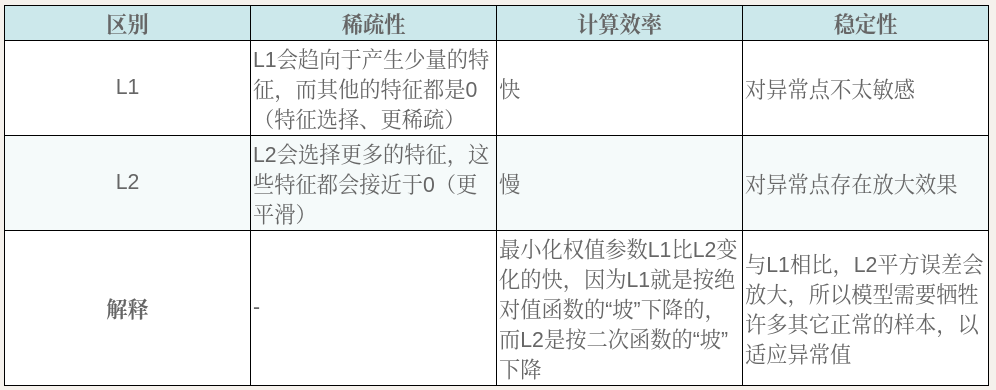
L1 和 L2 的区别？

  • L1：更稀疏、更快、更稳定
  • L2：更平滑、慢、不稳定

L1、L2 正则化为什么能防止过拟合？

  • L1 正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，一定程度防止过拟合 (overfitting) ，因为一个模型中真正重要的参数可能并不多
  • L2 正则化可以通过减小参数来防止模型过拟合 (overfitting)
  • 参数值越小说明模型越简单，因为有较大的参数值才能产生较大的导数

L1 正则化项是如何作用于权值 w 的步骤？

  • L1 正则化可以产生稀疏权值矩阵，即产生一个稀疏模型
  • 代价函数的梯度
  • 更新权重
  • 其中 α 学习速率 (learning rate)，sgn (w) 为 w 的正负号，当 w 大于 0 会减去一个正项，使 w 减小；当 w 小于 0 会减去一个负项，使 w 变大。因此 l1 正则化容易使 w 变为 0
  • 总得来说，l1 和 L2 正则化都是通过减小权值 w，使某些神经元的作用变小甚至可以勿略，从而降低网络模型的复杂度来防止过拟合。这与 dropout 通过以一定的概率丢弃神经元的做法在效果上是相似的。 也可以理解为：加了先验。在数据少的时候，先验知识可以防止过拟合。（因为模型复杂度变低）

L2 正则化项是如何作用于权值 w 的步骤？

  • L2 正则化可以通过减小参数来防止模过拟合 (overfitting)
  • 代价函数的梯度
  • 更新权重
  • 其中 α 为学习率，因为为非负项，因此 w 的系数是小于 1 的，在迭代更新中，w 会不断地减小。因此 l2 正则化又叫什么是权重衰减 (weight decay)?
  • 总得来说，l1 和 l2 正则化都是通过减小权值 w，使某些神经元的作用变小甚至可以勿略，从而降低网络模型的复杂度来防止过拟合。这与 dropout 通过以一定的概率丢弃神经元的做法在效果上是相似的。 也可以理解为：加了先验。在数据少的时候，先验知识可以防止过拟合。（因为模型复杂度变低）

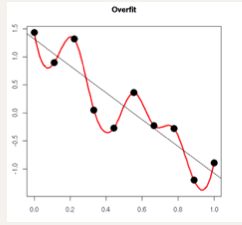
为什么参数小能降低过拟合？

  • 模型过于复杂是因为模型尝试去兼顾各个测试数据点， 导致模型函数如下图，处于一种动荡的状态， 每个点的到时在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。
  • 如果发过拟合 (overfitting)， 参数 θ 一般是比较大的值， 加入惩罚项后， 只要控制 λ 的大小，当 λ 很大时，θ1 到 θn 就会很小，即达到了约束数量庞大的特征的目的

正则化（L1、L2）与 Lasso 回归、Ridge 回归的关系？

  • Lasso 回归 Ridge 回归 (岭回归) 是分别在标准线性回归基础上加上 L1、L2 正则项的回归方法
  • 用以限制回归过程模型参数的解空间，可进行特征选择或避过拟合 (overfitting)