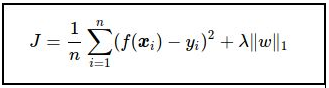套索回归 - Lasso_regression

发表于 更新于 分类于 ， 阅读次数： 本文字数： 2.4k 阅读时长 ≈ 2 分钟

在最小二乘的基础上增加对参数的约束，使得参数越靠近 0 越好

什么是套索回归？

  • 估计稀疏系数线性模型。它在某些情况下很有用，因为它倾向于选择具有较少非零系数的解决方案，从而有效地减少了给定解决方案所依赖的特征数量。因此，Lasso 及其变体是压缩感知领域的基础
  • 在数学上，它由一个带有正则化 (regularization) 项的线性模型组成。最小化的目标函数是，套索解决了 α∣∣w∣∣1\alpha ||w||_1 最小二乘惩罚的最小化问题，α\alpha 是常数，∣∣w∣∣1||w||_1 是一个系数向量的 L1 范

min⁡w12nsamples∣∣Xw−y∣∣22+α∣∣w∣∣1\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha ||w||_1}

  • Lasso 使用坐标下降作为算法来拟合系数
    1
    2
    3
    4
    5
    6
       >>> from sklearn import linear_model
       >>> reg = linear_model.Lasso(alpha=0.1)
       >>> reg.fit([[0, 0], [1, 1]], [0, 1])
    Lasso(alpha=0.1)
       >>> reg.predict([[1, 1]])
    array([0.8])

什么是 Lasso 回归？

  • 全称为 least absolute shrinkage and selection operator（Lasso），又译最小绝对值收敛和选择算子、套索算法
  • 在线性回归基础上加入 L1 正则化

Lasso 回归如何应用于特征选择？

  • 使用 L1 范数惩罚的线性模型具有稀疏解：它们的许多估计系数为零。当目标是降低数据的维度以与另一个分类器一起使用时，它们可以与 SelectFromModel 选择非零系数一起使用
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    >>> from sklearn.svm import LinearSVC
    >>> from sklearn.datasets import load_iris
    >>> from sklearn.feature_selection import SelectFromModel
    >>> X, y = load_iris(return_X_y=True)
    >>> X.shape
        (150, 4)
    >>> lsvc = LinearSVC(C=0.01, penalty="l1", dual=False).fit(X, y)
    >>> model = SelectFromModel(lsvc, prefit=True)
    >>> X_new = model.transform(X)
    >>> X_new.shape
        (150, 3)

什么是多任务套索？

  • 使用 L1/L2 混合范数作为正则化器训练的多任务套索回归， 目标函数如下，其中∣∣A∣∣Fro=∑ijaij2||A||_{\text{Fro}} = \sqrt{\sum_{ij} a_{ij}^2}
  • 使用 L1/L2 混合范数作为正则化器训练的多任务套索回归， 目标函数如下，其

12∗nsamples∗∣∣y−Xw∣∣22+alpha∗∣∣w∣∣1\frac {1} {2 * n_samples} * ||y - Xw||^2_2 + alpha * ||w||_1

min⁡W12nsamples∣∣XW−Y∣∣Fro2+α∣∣W∣∣21\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W - Y||_{\text{Fro}} ^ 2 + \alpha ||W||_{21}}

  • 使用 L1/L2 混合范数作为正则化器训练的多任务套索回归， 目标函数如下，其中 {INLINE_MATH_PLACEHOLDER}，$
    1
    2
    3
    4
    5
    6
    7
    8
    9
       >>> from sklearn import linear_model
       >>> clf = linear_model.MultiTaskLasso(alpha=0.1)
       >>> clf.fit([[0, 1], [1, 2], [2, 4]], [[0, 0], [1, 1], [2, 3]])
    MultiTaskLasso(alpha=0.1)
       >>> print(clf.coef_)
    [[0.         0.60809415]
    [0.         0.94592424]]
       >>> print(clf.intercept_)
    [-0.41888636 -0.87382323]

什么是 LARS 套索？

  • 使用 LARS 算法实现的套索模型，与基于坐标下降的实现不同，这会产生精确解，它是分段线性的，是其系数范数的函数，优化目标为 {INLINE_MATH_PLACEHOLDER}
    1
    2
    3
    4
    5
    6
       >>> from sklearn import linear_model
       >>> reg = linear_model.LassoLars(alpha=.1, normalize=False)
       >>> reg.fit([[0, 0], [1, 1]], [0, 1])
    LassoLars(alpha=0.1, normalize=False)
       >>> reg.coef_
    array([0.6..., 0.        ])