岭回归 - Ridge-regression 和分类

发表于 更新于 分类于 ， 阅读次数： 本文字数： 1.9k 阅读时长 ≈ 2 分钟

在最小二乘法的基础上，增加对参数的约束，要求参数越小越好

什么是 Ridge 回归 (岭回归)？

  • 在线性回归基础上加入 L2 正则化 ，通过对系数的大小施加惩罚来解决普通最小二乘法 (OLS) 的一些问题 ，岭系数最小化惩罚残差平方

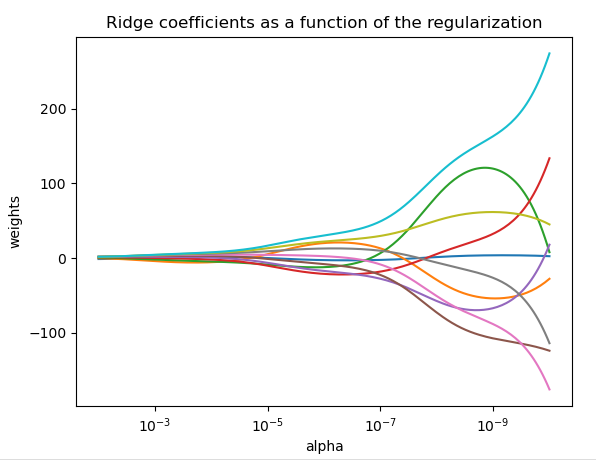
    min⁡w∣∣Xw−y∣∣22+α∣∣w∣∣22\min_{w} || X w - y||_2^2 + \alpha ||w||_2^2

  • 复杂度参数α≥0\alpha \geq 0 控制收缩量，值越大，收缩量越大，系数对共线性变得更加稳健。下图 当 α\alpha 非常大时，正则化效果在平方损失函数中占主导地位，并且系数趋于零。在路径的末端，随着 alpha 趋向于零并且解趋向于普通最小二乘法 (OLS)，系数表现出很大的振荡。在实践中，有必要以在两者之间保持平衡的方式调整 alpha

    1
    2
    3
    4
    5
    6
    >>> from sklearn.datasets import load_breast_cancer
    >>> from sklearn.linear_model import RidgeClassifier
    >>> X, y = load_breast_cancer(return_X_y=True)
    >>> clf = RidgeClassifier().fit(X, y)
    >>> clf.score(X, y)
        0.9595...

什么是带有内置交叉验证的岭回归？

  • 默认情况下，它执行高效的 Leave-One-Out 交叉验证
    1
    2
    3
    4
    5
    6
    7
    8
    >>> import numpy as np
    >>> from sklearn import linear_model
    >>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13))
    >>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
        RidgeCV(alphas=array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
              1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06]))
    >>> reg.alpha_
        0.01

简单描述岭回归算法？

  • 岭回归算法是一种专门用于共线性问题数据分析的有偏估计回归方法，实际上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价，获得回归系数更符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法

如何用最小角回归算法求解 Lasso 回归？

  • 前向选择（Forward Selection）算法：把 矩阵 X 看做 n 个 mx1 的向量 Xi (i=1,2,…n)，在 Y 的 X 变量 Xi (i =1,2,…n) 中，选择和目标 Y 最为接近 (余弦距离最大) 的一个变量 Xk，用 Xk 来逼近 Y
  • 前向梯度（Forward Stagewise）算法：在 Y 的 X 变量 Xi (i =1,2,…n) 中，选择和目标 Y 最为接近 (余弦距离最大) 的一个变量 Xk，用 Xk 来逼近 Y，但是前向梯度算法不是粗暴的用投影，而是每次在最为接近的自变量 Xt 的方向移动一小步，然后再看残差 Yyes 和哪个 Xi (i =1,2,…n) 最为接近
  • 最小角回归 (Least Angle Regression， LARS) 算法：运用到了前向选择法（选取余弦距离最小的值进行投影，计算残差，迭代这个过程，直到残差达到我们的较小值或者已经遍历了整个变量）和前向梯度算法（选取余弦距离最小的值的样本方向进行移动一定距离，计算残差，重复这个迭代过程）的综合，做法就是取投影方向和前向梯度算法的残差方向形成的角的平分线方向，进行移动。对前向梯度算法和前向选择算法做了折中，保留了前向梯度算法一定程度的精确性，同时简化了前向梯度算法一步步迭代的过程

如何用坐标下降算法求解 Lasso 回归？

  • Lasso 回归也叫做线性回归的 L1 正则化，由于 L1 范数用的是绝对值之和，在零点处不可求导，所以使用非梯度下降法进行求解，如 坐标轴下降法和最小角回归法
  • 每次选择一个维度进行参数更新，维度的选择可以是随机的或者是按顺序。 当一轮更新结束后，更新步长的最大值少于预设阈值时，终止迭代
  • 坐标下降优化方法是一种非梯度优化算法。在整个过程中依次循环使用不同的坐标方向进行迭代，一个周期的一维搜索迭代过程相当于一个梯度迭代
  • 梯度下降法是利用目标函数的导数（梯度）来确定搜索方向的，该梯度方向可能不与任何坐标轴平行。而坐标下降法是利用当前坐标方向进行搜索，不需要求目标函数的导数，只按照某一坐标方向进行搜索最小值，两者都是迭代方法