统计推断之参数假设检验

假设建议是根据现有试验，推断出其满足的分布，一般是假设试验满足分布，然后在置信度区域内计算随机变量，如何随机变量出现在该置信度接受区域内，则接受假设，否则拒绝假设

• 什么是参数假设检验?

  • 所谓假设检验就是对总体分布中的某个参数或者分布的形式作出某种假设，利用抽取样本提供的信息，构造适合的统计量，再根据小概率事件进行检验，以作出统计推断
  • 常用的假设检验方法有U检验法，t检验法，$\chi^2$ 检验法，F检验法

• 检验方法适应范围

  • Z检验的条件：样本来自正态分布且方差已知的情况
  • T检验的条件：样本来自正态分布且方差未知的情况，两独立样本T检验主要用于检验两个样本的平均数差异
  • U检验的条件：应用条件和t检验应用条件基本一致， 只是大样本时用u检验 ，小样本时用t检验，t检验可以代替U检验

• 假设检验的原理？

  • 
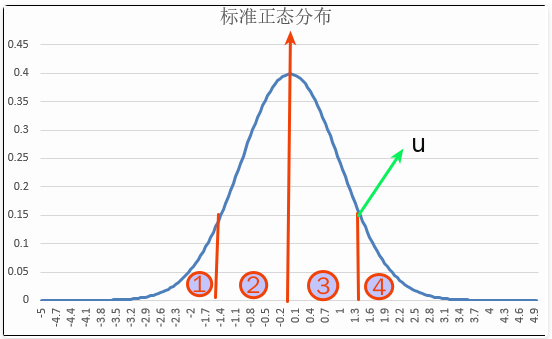
  • 对于给定的置信度 $1- \alpha$ ，我们算得统计量 $|U|< u_{\alpha/2}$,并由此得出未知参数的置信区间。图中的 2 加 3 为置信区间。
  • 对于假设检验，给定显著性水平（即为置信区间中的 $\alpha$），构造统计量后，代入具体一次抽样的数据和假设条件，如果统计量的值在图中 2 加 3 的区域下，说明该次抽样是发生在大概率的条件下，则接受假设条件，否则统计量落在 3 加 4 的区域内，拒绝假设条件。通常 3 加 4 区域为拒绝域, 1 加 2 为接受域，依据统计量落的范围决定―接受/拒绝假设条件

• 什么是原假设与备择假设？

  • 把检验的假设称为原假设；把原假设的对立面称为备择假设

• 什么是显著性检验与显著性水平？

  • 假设检验有两类错误，分别是：$P(拒绝H_0|H_0为真)=\alpha$ 和$P(接受H_0|H_0为假)=\beta$，通常显示$\alpha$的最大上界而不考虑$\beta$的问题称为假设检验，并将$\alpha$的最大上界称为假设检验的显著性水平

• 什么是双侧边假设检验与单侧边假设检验？

  • 针对原假设的假设形式而言

• 什么是拒绝域与临界点?

  • 拒绝域是统计量的范围，临界点是拒绝域的边界

• 假设检验一般步骤？

  • 提出假设：提出原假设$H_0$ 和备择假设$H_1$
  • 建立合适的统计量，选择检验统计量并确定其分布
  • 确定拒绝域：现给定的显著性水平下，确定$H_0$关于统计量的拒绝域
  • 计算：计算样本点对于统计量的值
  • 判断：若统计量落在拒绝域内，则拒绝$H_0$，否则接受$H_0$

• 方差$\sigma^2$ 已知单个正态总体均值检验？

  • 当方差$\sigma^2$ 已知，给定显著性水平$\alpha$ ，假设$H_0:\mu=\mu_0$ ,其拒绝域为：

    $$|U|=|\frac{\overline X -\mu_0}{\sigma/\sqrt{n}}|>u_{\alpha/2}$$

  • 其中$\frac{\overline X -\mu_0}{\sigma/\sqrt{n}} - N(0,1)$,$\overline X$和$n$来自样本，$\mu_0$是假设。

  • 所以说，上面统计量在某个抽样和假设下的值是可以算出来的，如果该值满足上面的式子（即落在拒绝域内），则拒绝假设$H_0:\mu=\mu_0$

  • 例子

  • 这种利用标准正态分布的统计量进行检验的方法称为:U检验法

• 方差$\sigma^2$ 未知的单个正态总体均值检验？

  • 在方差未知的情况下，使用样本的方差进行分析，可构造其统计量为 $T=\frac {\overline X - \mu} {S / \sqrt n} - t(n-1)$ ， 拒绝域为 $|t|=|\frac {\overline X - \mu_0} {S / \sqrt n} | \geq t_{\alpha/2}(n-1)$
  • 
  • 这种利用t分布的统计量进行检验的方法称为:t检验法

• 单个正态总体方差检验？

  • 设X-N($\mu,\sigma$ ),抽样一组数据，得到其均值和方差为$\overline X,S^2$ ,原假设：$H_0:\sigma=\sigma_0$; 备择假设：$H_1:\sigma \neq \sigma_0$,其中$\sigma_0$为已知常数。
  • 可知：$\chi^2=\frac {n-1} {\sigma_0^2} S^2 - \chi^2(n-1)$ , 给定显著性水平$\alpha$，得到以下拒绝域$\chi^2=\frac {n-1} {\sigma_0^2} S^2 \leq \chi_{1-\alpha/2}^2(n-1)\\ \chi^2=\frac {n-1} {\sigma_0^2} S^2 \geq \chi_{\alpha/2}^2(n-1)$
  • 

• 两个正态总体均值差检验，方差$\sigma_1^2,\sigma_2^2$ 已知

  • 提出假设：$H_0:\mu_1-\mu_2=\mu_0,H1:\mu_1-\mu_2 \neq \mu_0$ ,其中$\mu_0$ 已知
  • 当$H_0$为真时$U=\frac{\overline X - \overline Y - \mu_0}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}} - N(0,1)$
  • 给定显著性水平$\alpha$，得到以下拒绝域

    $$|u|=|\frac{\overline x - \overline y - \mu_0}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}}| > u_{\alpha/2}$$

• 两个正态总体均值差检验，方差$\sigma_1^2,\sigma_2^2$ 未知，并且$\sigma_1^2=\sigma_2^2=\sigma$

  • 提出假设：$H_0:\mu_1-\mu_2=\mu_0,H1:\mu_1-\mu_2 \neq \mu_0$ ,其中$\mu_0$ 已知

  • 当$H_0$为真时

    $$t=\frac{\overline X - \overline Y - \mu_0}{S_w\sqrt{1/n_1+1/n_2}} -t(n_1+n_2-2)$$

  • 给定显著性水平$\alpha$，得到以下拒绝域

    $$|t|=|\frac{\overline X - \overline Y - \mu_0}{S_w\sqrt{1/n_1+1/n_2}}| > t_{\alpha/2}(n_1+n_2-2)$$

• 两个正态总体方差相等的假设检验？

  • 假设有$N(\mu_1,\sigma_1)和N(\mu_2,\sigma_2)$ 两个正态分布，从其中各抽样一次，算得样本方差为$S_1^2,S_2^2$

  • 提出假设：$H_0:\sigma_1=\sigma_2,H1:\sigma_1 \neq \sigma_2$

  • 当$H_0$为真时

    $$F=\frac{S_1^2}{S_2^2}-F(n_1-1)(n_2-1)$$

  • 给定显著性水平$\alpha$，得到以下拒绝域$F < F_{1-\alpha/2}(n_1-1,n_2-1)$ 或$F > F_{\alpha/2}(n_1-1,n_2-1)$