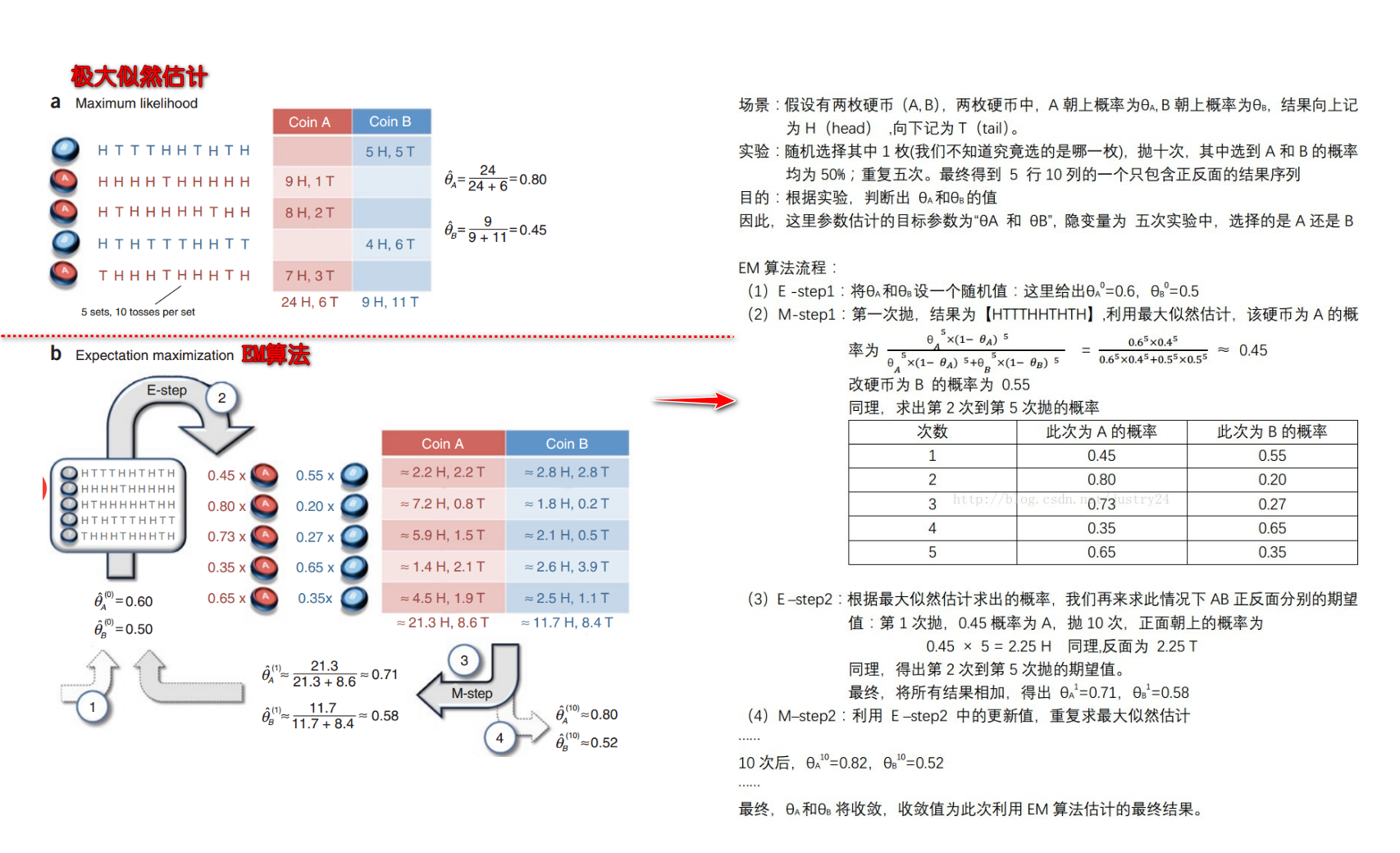
期望最大化 - EM

本文讲解了经典的 EM 算法，通过假设初始值，不断迭代优化参数，最终求出参数，重点理解 EM 算法的 E 步和 M 步

什么是期望最大化 (Expectation-Maximum, EM) ？

• EM 算法是一种迭代优化策略，由于它的计算方法中每一次迭代都分两步，其中一个为期望步（E 步），另一个为极大步（M 步），它是一个基础算法，是很多机器学习领域算法的基础，比如、混合高斯模型、聚类、HMM 等等
• EM 算法作用：通过观察的数据更新初始变量值，使得该值越来越符合发生的事实 (观察)
• K-Means 算法也是采样 EM 算法优化的，在 K-Means 聚类时，每个聚类簇的质心是隐含数据。我们会假设 K 个初始化质心，即 EM 算法的 E 步；然后计算得到每个样本最近的质心，并把样本聚类到最近的这个质心，即 EM 算法的 M 步。重复这个 E 步和 M 步，直到质心不再变化为止，这样就完成了 K-Means 聚类

采用 EM 算法求解的模型有哪些，为什么不用牛顿法或梯度下降法？

• 用 EM 算法求解的模型一般有 GMM 或者协同过滤，K-means 其实也属于 EM
• EM 算法一定会收敛，但是可能收敛到局部最优。由于求和的项数将随着隐变量的数目指数上升，会给梯度计算带来麻烦