B05 - 图像处理 - 图像滤波

发表于 2022-04-09 更新于 2025-01-18 分类于 3-编程实践， E-OpenCV ， OpenCV使用指南阅读次数：本文字数： 12k 阅读时长 ≈ 11 分钟

对图像进行空间域滤波，凸显带有特定特征的区域，比如高通滤波用于找边缘，低通滤波用于过滤噪声，类似卷积的过程，在滤波核范围内变换像素值；
将空间域的图片，按照不同的频率系数将其转换为频率域特征，然后在该域内处理数据，其思路是傅里叶变换，类似泰勒公式的展开过程

什么是 “空间域” 图像滤波？

图像滤波是在尽可能保留图像细节特征的条件下对目标图像的噪声进行抑制，是常用的图像预处理操作
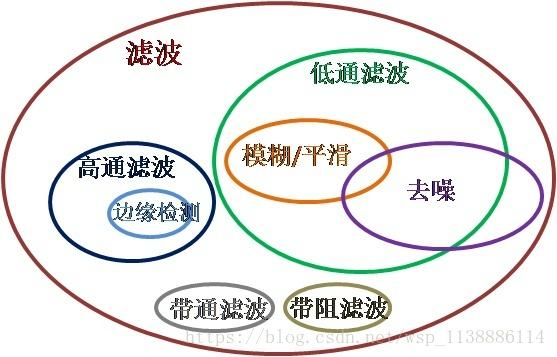
空间域和频率域线性滤波器可以分为四类：低通滤波器、高通滤波器、带通滤波器和带阻滤波器，后三类滤波器都可以由低通滤波器构造
滤波器应用：(1) 消除图像中混入的噪声；(2) 识别图像中的特征，如边缘检测

空间域的图像滤波和频率域的图像滤波的区别？

空间域图像滤波：图像与各种空间滤波器（模板、核）的卷积
频率域图像滤波：先将图像进行傅里叶变换，然后在变换域进行处理，最后进行傅里叶反变换转换回空间域
空间域滤波器和频率域滤波器形成一个傅里叶变换对，也就是说，空间域滤波器和频率域滤波器实际上是相互对应的，有些空间域滤波器在频率域通过傅里叶变换实现会更方便、更快速。例如，空间域的拉普拉斯滤波器就是频率域的高通滤波

\begin{array}{ll}\operatorname{f(x,y)}\otimes\operatorname{h(x,y)}\Leftrightarrow\operatorname{F(u,v)H(u,v)}\\ \operatorname{f(x,y)h(x,y)}\Leftrightarrow\operatorname{F(u,v)}\otimes\operatorname{H(u,v)}\quad\end{array}

低通滤波器、高通滤波器、带通滤波器和带阻滤波器的区别？

以下传递函数都可以由一个低通滤波器传递函数通过线性变换得到
低通滤波器： $\operatorname{lp}(x,y)$
高通滤波器： $\mathrm{hp(x,y)=\delta(x,y)-lp(x,y)}$
带通滤波器： $\mathrm{br}(x,y)=\mathrm{lp}_1(x,y)+\mathrm{hp}_2(x,y)$
带阻滤波器： $\mathrm{bp(x,y)=\delta(x,y)-br(x,y)}$

什么是高通滤波和低通滤波？

图像在频域里面，频率低的地方说明它是比较平滑的，因为平滑的地方灰度值变化比较小，而频率高的地方通常是边缘或者噪声，因为这些地方往往是灰度值突变的
高通滤波：保留频率比较高的部分，即突出边缘，常用于检测图像尖锐、变化幅度大的区域；比如边缘检测，轮廓提取
低通滤波：保留频率比较低的地方，即平滑图像，弱化边缘，消除噪声

高通滤波的原理？

高通滤波，意思就是让高频部分通过，留下低频部分；而衍生到图像上面来理解，一张图片的像素一般来说，在轮廓的地方像素值高，而在其他部分像素值低，例如一张图像上面的人像，人像的轮廓之所以我们能够看出来就是因为与周围像素值相差过大，频率高，周围像素值低，频率低，形成像素差，从而我们肉眼可以分辨

低通滤波器的原理？

低通滤波其实就是将频域图中心部分保留，将外围部分过滤，衍生到图像中就是将高频区域 (255，亮) 对应的像素值设置为低频（0，黑色），低频区域对应的像素值不改变。可以用于去噪声，包括去椒盐噪声和高斯噪声

在 OpenCV 有哪些低通滤波器？

线性滤波
- 方框滤波
- 均值滤波
- 高斯滤波
非线性滤波
- 中值滤波
- 双边滤波
非局部去躁
- 彩色图非局部去躁
- 灰度图非局部去躁

OpenCV 有哪些高通滤波器？

拉普拉斯算子
Sobel 算子
Canny 算子

如何自定义线性滤波器？

自定义卷积核，并使用 cv: :filter2D 进行滤波

什么是图像锐化？

图像锐化的目的是增强图像的灰度跳变部分，使模糊的图像变得清晰。图像锐化也称为高通滤波，通过和增强高频，衰减和抑制低频。图像锐化常用于电子印刷、医学成像和工业检测
图像模糊通过平滑（加权平均）来实现，类似于积分运算。图像锐化则通过微分运算（有限差分）实现，使用一阶微分或二阶微分都可以得到图像灰度的变化值
灰度调变规律：1）恒定灰度区域，一阶导数为零，二阶导数为零；2）灰度台阶或斜坡起点区域，一阶导数非零，，二阶导数非零；3）灰度斜坡区域，一阶导数非零，二阶导数为零

如何实现图像的锐化？

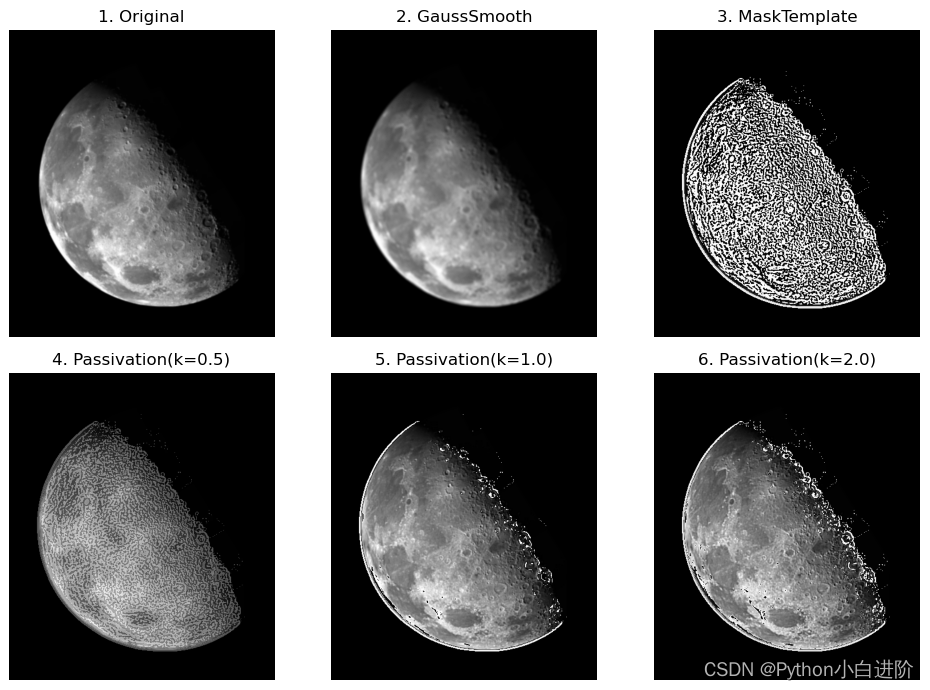
从原始图像中减去一幅平滑处理的钝化图像，也可以实现图像锐化效果，称为钝化掩蔽。当 k>1 时，实现高提升滤波；当 k=1 时，实现钝化掩蔽；k<1 时，减弱钝化掩

\begin{gathered}\mathrm{g}_{\mathrm{mask}}(x,y)=\mathrm{f}(x,y)-\tilde{f}(x,y) \\\mathrm{g(x,y)=f(x,y)+k*g_{\mathrm{mask}}(x,y),k>0}\end{gathered}

实现过程：（1）对原始图像进行平滑处理，得到平滑图像；（2）从原始图像中减去平滑图像，产生掩蔽模板；（3）将原始图像与掩蔽模板加权相加，得到钝化掩蔽

img = cv2.imread("../images/Fig0338a.tif", flags=0)
# 对原始图像进行平滑，GaussianBlur(img, size, sigmaX)
imgGauss = cv2.GaussianBlur(img, (5,5), sigmaX=5)
imgGaussNorm = cv2.normalize(imgGauss,dst=None,alpha=0,beta=255,norm_type=cv2.NORM_MINMAX)
# 掩蔽模板：从原始图像中减去平滑图像
imgMask = img - imgGaussNorm
passivation1 = img + 0.6 * imgMask  # k<1 减弱钝化掩蔽
imgPas1 = cv2.normalize(passivation1, None, 0, 255, cv2.NORM_MINMAX)
passivation2 = img + imgMask  # k=1 钝化掩蔽
imgPas2 = cv2.normalize(passivation2, None, 0, 255, cv2.NORM_MINMAX)
passivation3 = img + 2 * imgMask  # k>1 高提升滤波
imgPas3 = cv2.normalize(passivation3, None, 0, 255, cv2.NORM_MINMAX)

使用低通滤波器实现图像抗混叠？

混叠分为空间混叠和时间混叠。空间混叠是由欠取样造成的，在陌生重复的图像中较为明显。时间混叠与动态图像序列中图像的时间间隔相关，如辐条倒转的 “车轮效应”。空间混叠的主要问题是会引入伪影，即原始图像中未出现的线条锯齿、虚假高光和频率模式

对图像进行缩放都会引入混叠。图像放大可以视为过取样，使用双线性、双三次内插可以降低图像放大中的混叠。图像缩小可以视为欠取样，混叠通常更为严重。为了降低混叠，在重取样前要使用低通滤波器来平滑，以衰减图像的高频分量，可以有效地抑制混叠，但图像的清晰度也有所下降

imgGray = cv2.imread("../images/Fig0417a.tif", flags=0)  # flags=0 读取为灰度图像
height, width = imgGray.shape[:2]  # 图片的高度和宽度
# 先缩小图像，再放大图像
imgZoom1 = cv2.resize(imgGray, (int(0.33*width), int(0.33*height)))
imgZoom2 = cv2.resize(imgZoom1, None, fx=3, fy=3, interpolation=cv2.INTER_AREA)
# 先对原图像进行5x5的低通滤波，再缩小图像，再放大图像
kSize = (5, 5)
imgBoxFilter = cv2.boxFilter(imgGray, -1, kSize)  # cv2.boxFilter 方法
imgZoom3 = cv2.resize(imgBoxFilter, (int(0.33*width), int(0.33*height)))
imgZoom4 = cv2.resize(imgZoom3, None, fx=3, fy=3, interpolation=cv2.INTER_AREA)
show_images([imgGray,imgZoom2,imgZoom4])

什么是差分滤波？

对于图像亮度急剧变化的边缘有提取效果，可以获得邻近像素的差值，其滤波矩阵如下

什么是 Non-local means (NLM)？

局部降噪算法：均值滤波、中值滤波等，都是使用一个固定的 Kernel 对图像进行一个滤波操作。这种算法被称之为局部算法。“局部均值” 滤波器采用目标像素周围的一组像素的平均值来平滑图像
NLM：图像去噪的一种算法。与 “局部均值” 滤波器不同，非局部均值过滤采用图像中所有像素的平均值，并根据这些像素与目标像素的相似程度进行加权。与局部均值算法相比，这导致滤波后清晰度更高，图像中的细节损失更少
NLM 的实现：通过在图像块中进行搜索，通过计算滑动窗口与指定窗口的欧氏距离，从而它们之间的相似程度，从而确定加权平均的值，进行滤波操作，其中 $W(i,j)$ 表示加权平均的 kernel 值，由两个块之间的相似度决定； Opencv 使用 cv: : fastNlMeansDenoisingColored 可快速执行 NL

NL[v](i)=\sum\limits_{j\in I}w(i,j)v(j),

什么是频率域图像滤波？

图像滤波是在尽可能保留图像细节特征的条件下对目标图像的噪声进行抑制，是常用的图像预处理操作
频率域图像处理先将图像进行傅里叶变换，然后在变换域进行处理，最后进行傅里叶反变换转换回空间域
图像滤波不仅可以在空间域进行还可以在频率域进行。空间滤波是图像与各种空间滤波器（模板、核）的卷积，而空间卷积的傅里叶变换是频率域中相应变换的乘积，因此频率域滤波是频率域滤波器（传递函数）与图像的傅里叶变换相乘

频率域滤波的理论基础？

对信号或图像进行傅里叶变换后，可以得到信号或图像的低频信息和高频信息。低频信息对应图像中缓慢变化的灰度分量，高频信息则对应尖锐变化的灰度分量
低频滤波器：本质上就是中心低频置 1（白色）四周高频置 0（黑色）的矩阵，低通滤波遮罩 mask 与图像傅里叶变换 dftShift 相乘，就使傅里叶变换的高频部分为 0，从而屏蔽原始图像中高频信号，实现了低通滤波
高通滤波器：类似地，将本例程中的低通滤波矩形窗口遮罩反向，改为中心高频置 0（黑色）四周低频置 1（白色），就是一种高通滤波器，可以实现图像锐化和边缘提取

低通滤波就是保留傅里叶变换的低频信息、削弱高频信息，而高通滤波则是保留傅里叶变换的高频信息、削弱低频信息

imgGray = cv2.imread(".tif", flags=0)  # flags=0 读取为灰度图像
height, width = imgGray.shape[:2]  # 图片的高度和宽度
centerY, centerX = int(height/2), int(width/2)  # 图片中心
# （1）首先对图像进行傅里叶变换
imgFloat32 = np.float32(imgGray)  # 将图像转换成 float32
dft = cv2.dft(imgFloat32, flags=cv2.DFT_COMPLEX_OUTPUT)  # 傅里叶变换
dftShift = np.fft.fftshift(dft)  # 将低频分量移动到频域图像的中心
d = [20, 40, 80]
for i in range(3):
	# 构造低通滤波器矩形窗口遮罩 mask
	mask = np.zeros((height, width, 2), np.uint8)
	mask[centerY-d[i]:centerY+d[i], centerX-d[i]:centerX+d[i]] = 1  # 设置低通滤波矩形窗口遮罩，过滤高频
	maskAmp = np.uint8(np.sqrt(np.power(mask[:,:,0], 2) + np.power(mask[:,:,1], 2)))
	print("d={}, maskAmp: max={}, min={}".format(d[i],maskAmp.max(), maskAmp.min()))
	# （2）然后在频率域修改傅里叶变换
	dftMask = dftShift * mask  # 修改傅里叶变换实现滤波
	# （3）最后通过傅里叶逆变换返回空间域
	iShift = np.fft.ifftshift(dftMask)  # 将低频逆转换回图像四角
	iDft = cv2.idft(iShift)  # 逆傅里叶变换
	imgRebuild = cv2.magnitude(iDft[:,:,0], iDft[:,:,1])  # 重建图像
	show_images([maskAmp,imgRebuild])

频率域图像滤波的一般步骤？

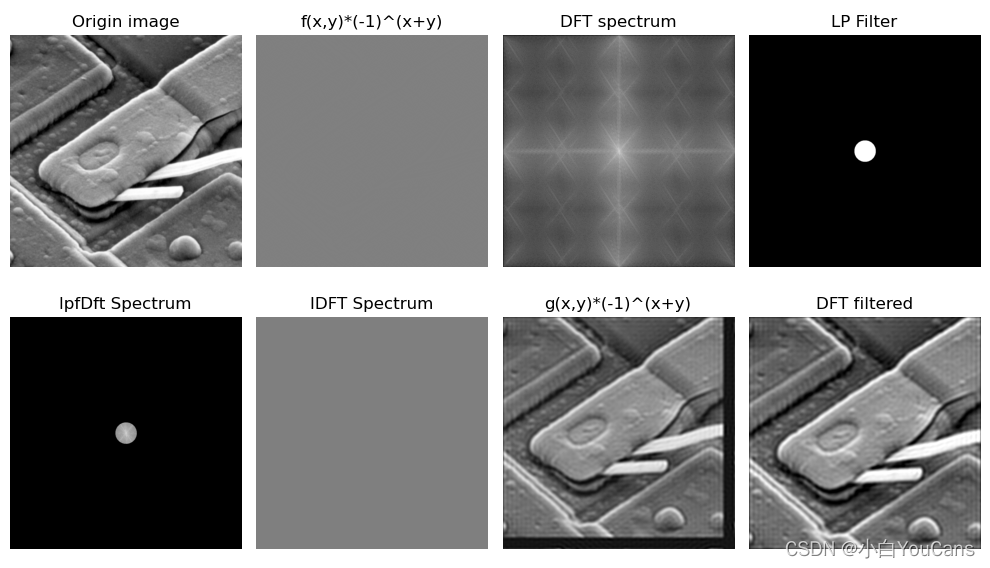
首先对原图像 f (x, y) 经傅里叶变换为 F (u, v)，然后用适当的滤波器函数 H (u, v) 对傅里叶变换 F (u, v) 的频谱成分进行修改，最后通过傅里叶逆变换（IDFT）返回空间域，得到增强的图像 g (x, y)

以下例子使用高斯低通滤波作为 H (u, v) 对频域进行滤波

# (1) 读取原始图像
# imgGray = cv2.imread("../images/imgLena.tif", flags=0)  # flags=0 读取为灰度图像
imgGray = cv2.imread("../images/Fig0431.tif", flags=0)  # flags=0 读取为灰度图像
imgFloat32 = np.float32(imgGray)  # 将图像转换成 float32
rows, cols = imgGray.shape[:2]  # 图片的高度和宽度
# (2) 中心化, centralized 2d array f(x,y) * (-1)^(x+y)
mask = np.ones(imgGray.shape)
mask[1::2, ::2] = -1
mask[::2, 1::2] = -1
fImage = imgFloat32 * mask  # f(x,y) * (-1)^(x+y)
# (3) 快速傅里叶变换
rPadded = cv2.getOptimalDFTSize(rows)  # 最优 DFT 扩充尺寸
cPadded = cv2.getOptimalDFTSize(cols)  # 用于快速傅里叶变换
dftImage = np.zeros((rPadded, cPadded, 2), np.float32)  # 对原始图像进行边缘扩充
dftImage[:rows, :cols, 0] = fImage  # 边缘扩充，下侧和右侧补0
cv2.dft(dftImage, dftImage, cv2.DFT_COMPLEX_OUTPUT)  # 快速傅里叶变换
dftAmp = cv2.magnitude(dftImage[:,:,0], dftImage[:,:,1])  # 傅里叶变换的幅度谱 (rPad, cPad)
dftAmpLog = np.log(1.0 + dftAmp)  # 幅度谱对数变换，以便于显示
dftAmpNorm = np.uint8(cv2.normalize(dftAmpLog, None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
# (4) 构建低通滤波器 传递函数
# 找到傅里叶谱最大值的位置
minValue, maxValue, minLoc, maxLoc = cv2.minMaxLoc(dftAmp)
rPadded, cPadded = dftImage.shape[:2]  # 快速傅里叶变换的尺寸, 原始图像尺寸优化
u, v = np.mgrid[0:rPadded:1, 0:cPadded:1]
Dsquare = np.power((u-maxLoc[1]), 2.0) + np.power((v-maxLoc[0]), 2.0)
D0 = 50  # radius
D = np.sqrt(Dsquare)
lpFilter = np.zeros(dftImage.shape[:2], np.float32)
lpFilter[D <= D0] = 1  # 理想低通滤波 (Idea low pass filter)
# (5) 在频率域修改傅里叶变换: 傅里叶变换 点乘 低通滤波器
# rPadded, cPadded = dftImage.shape[:2]  # 快速傅里叶变换的尺寸, 原始图像尺寸优化
dftLPfilter = np.zeros(dftImage.shape, dftImage.dtype)  # 快速傅里叶变换的尺寸(优化尺寸)
for i in range(2):
	dftLPfilter[:rPadded, :cPadded, i] = dftImage[:rPadded, :cPadded, i] * lpFilter
# 低通傅里叶变换的傅里叶谱
lpDftAmp = cv2.magnitude(dftLPfilter[:, :, 0], dftLPfilter[:, :, 1])  # 傅里叶变换的幅度谱
lpDftAmpLog = np.log(1.0 + lpDftAmp)  # 幅度谱对数变换，以便于显示
lpDftAmpNorm = np.uint8(cv2.normalize(lpDftAmpLog, None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
# (6) 对低通傅里叶变换 执行傅里叶逆变换，并只取实部
idft = np.zeros(dftAmp.shape, np.float32)  # 快速傅里叶变换的尺寸(优化尺寸)
cv2.dft(dftLPfilter, idft, cv2.DFT_REAL_OUTPUT + cv2.DFT_INVERSE + cv2.DFT_SCALE)
# (7) 中心化, centralized 2d array g(x,y) * (-1)^(x+y)
mask2 = np.ones(dftAmp.shape)
mask2[1::2, ::2] = -1
mask2[::2, 1::2] = -1
idftCen = idft * mask2  # g(x,y) * (-1)^(x+y)
# (8) 截取左上角，大小和输入图像相等
result = np.clip(idftCen, 0, 255)  # 截断函数，将数值限制在 [0,255]
lpResult = result.astype(np.uint8)
lpResult = lpResult[:rows, :cols]
show_images([imgGray,fImage,dftAmpNorm,lpFilter,lpDftAmpNorm,idft,idftCen,lpResult])

频率域高斯低通滤波过程？

空间域高斯滤波器的计算量随着模板的增大而增大，而频率域高斯滤波的计算量独立于滤波函数

高斯滤波器的滤波效果随着样值点到傅里叶变换中心的距离的变化而变化，当距离增大时滤波效果变好

imgGray = cv2.imread("../images/imgLena.tif", flags=0)  # flags=0 读取为灰度图像
# （1）首先对图像进行傅里叶变换
imgFloat32 = np.float32(imgGray)  # 将图像转换成 float32
dft = cv2.dft(imgFloat32, flags=cv2.DFT_COMPLEX_OUTPUT)  # 傅里叶变换
dftShift = np.fft.fftshift(dft)  # 将低频分量移动到频域图像的中心
rows, cols = imgGray.shape[:2]  # 图片的高度和宽度
sigma2 = [0.5, 0.09, 0.01]  # square of sigma
for i in range(3):
	# 构造高斯滤波器遮罩：# Gauss = 1/(2*pi*s2) * exp(-(x**2+y**2)/(2*s2))
	x, y = np.mgrid[-1:1:2.0 / rows, -1:1:2.0 / cols]
	z = 1 / (2 * np.pi * sigma2[i]) * np.exp(-(x ** 2 + y ** 2) / (2 * sigma2[i]))
	zNorm = np.uint8(cv2.normalize(z, None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
	maskGauss = np.zeros((rows, cols, 2), np.uint8)
	maskGauss[:,:,0] = zNorm
	maskGauss[:,:,1] = zNorm
	print(maskGauss.shape, maskGauss.max(), maskGauss.min())
	# （2）然后在频率域修改傅里叶变换
	dftTrans = dftShift * maskGauss  # 修改傅里叶变换实现滤波
	# （3）最后通过傅里叶逆变换返回空间域
	ishift = np.fft.ifftshift(dftTrans)  # 将低频逆转换回图像四角
	idft = cv2.idft(ishift)  # 逆傅里叶变换
	imgRebuild = cv2.magnitude(idft[:,:,0], idft[:,:,1])  # 重建图像
	show_images([maskGauss[:,:,0],imgRebuild])

OpenCV 如何对图像进行傅里叶变换？

OpenCV 中的 cv.Dft () 函数也可以实现图像的傅里叶变换，cv.Idft () 函数实现图像傅里叶逆变换

imgGray = cv2.imread("../images/Fig0424a.tif", flags=0)  # flags=0 读取为灰度图像
# cv2.dft 实现图像的傅里叶变换
imgFloat32 = np.float32(imgGray)  # 将图像转换成 float32
dft = cv2.dft(imgFloat32, flags=cv2.DFT_COMPLEX_OUTPUT)  # 傅里叶变换
dftShift = np.fft.fftshift(dft)  # 将低频分量移动到频域图像的中心
# 幅度谱
# ampSpe = np.sqrt(np.power(dft[:,:,0], 2) + np.power(dftShift[:,:,1], 2))
dftAmp = cv2.magnitude(dft[:,:,0], dft[:,:,1])  # 幅度谱，未中心化
dftShiftAmp = cv2.magnitude(dftShift[:,:,0], dftShift[:,:,1])  # 幅度谱，中心化
dftAmpLog = np.log(1 + dftShiftAmp)  # 幅度谱对数变换，以便于显示
# 相位谱
phase = np.arctan2(dftShift[:,:,1], dftShift[:,:,0])  # 计算相位角(弧度制)
dftPhi = phase / np.pi*180  # 将相位角转换为 [-180, 180]
print("dftMag max={}, min={}".format(dftAmp.max(), dftAmp.min()))
print("dftPhi max={}, min={}".format(dftPhi.max(), dftPhi.min()))
print("dftAmpLog max={}, min={}".format(dftAmpLog.max(), dftAmpLog.min()))
# cv2.idft 实现图像的逆傅里叶变换
invShift = np.fft.ifftshift(dftShift)  # 将低频逆转换回图像四角
imgIdft = cv2.idft(invShift)  # 逆傅里叶变换
imgRebuild = cv2.magnitude(imgIdft[:,:,0], imgIdft[:,:,1])  # 重建图像
show_images([imgGray,dftPhi,imgRebuild,dftAmp,dftShiftAmp,dftAmpLog])

Opencv 如何进行快速傅里叶变换？

傅里叶变换在理论上需要 $O(MN)^2$ 次运算，非常耗时；快速傅里叶变换只需要 $O (MNlog (MN)))$ 次运算就可以完成。做法是 cv. Dft () 对于行数和列数都可以分解为 $2^p\times 3^q\times 5^r$ 的矩阵的计算性能最好。为了提高运算性能，可以对原矩阵的右侧和下方补 0，以满足该分解条件

cv. GetOptimalDFTSize () 函数可以实现图像的最优 DFT 尺寸扩充，适用于 cv. Dft () 和 np. Fft. Fft 2 ()

imgGray = cv2.imread("../images/Fig0429a.tif", flags=0)  # flags=0 读取为灰度图像
rows,cols = imgGray.shape[:2]  # 图像的行(高度)/列(宽度)
# 快速傅里叶变换(要对原始图像进行矩阵扩充)
rPad = cv2.getOptimalDFTSize(rows)  # 最优 DFT 扩充尺寸
cPad = cv2.getOptimalDFTSize(cols)  # 用于快速傅里叶变换
imgEx = np.zeros((rPad,cPad,2),np.float32)  # 对原始图像进行边缘扩充
imgEx[:rows,:cols,0] = imgGray  # 边缘扩充，下侧和右侧补0
dftImgEx = cv2.dft(imgEx, cv2.DFT_COMPLEX_OUTPUT)  # 快速傅里叶变换
# 傅里叶逆变换
idftImg = cv2.idft(dftImgEx)  # 逆傅里叶变换
idftMag = cv2.magnitude(idftImg[:,:,0], idftImg[:,:,1])  # 逆傅里叶变换幅值
# 矩阵裁剪，得到恢复图像
idftMagNorm = np.uint8(cv2.normalize(idftMag, None, 0, 255, cv2.NORM_MINMAX))  # 归一化为 [0,255]
imgRebuild = np.copy(idftMagNorm[:rows, :cols])
show_images([imgGray,cv2.normalize(dftAmpLog, None, 0, 255, cv2.NORM_MINMAX),imgRebuild])

参考：