GFL

本文针对 anchor-free 模型最近新增 IOU 预测分支优化，提出 IOU 分支与分类分支联合优化 + GFL 的损失函数，实现更高的预测效果

Abstract

One-stage 的目标检测任务包含分类和回归，其中分类使用 Focal loss 优化，回归任务通常学习一个 Dirac delta distribution。近期还新增一个评估定位效果的分支，得到的结果作为分类分支的补充，以便提高目标检测的性能。也就是目标检测模型有 3 个输出：质量估计、分类及定位，但是现有方法存在以下问题：（1）质量评估和分类的不一致使用（训练时单独优化，测试时联合使用）；（2）当存在不确定性或歧义定位时，现有定位不灵活的 Dirac delta distribution 无法解决。

GFL 将质量评估整合到分类预测向量中，形成质量和分类的联合表示，并使用向量表示框位置的任意分布，解决以上问题。由此提出的方法命名为广义焦点损失 (GFL)，它将 Focal loss 从离散形式推广到连续版本

Introduction

1. 质量估计和分类分数在训练、推理时使用不一致

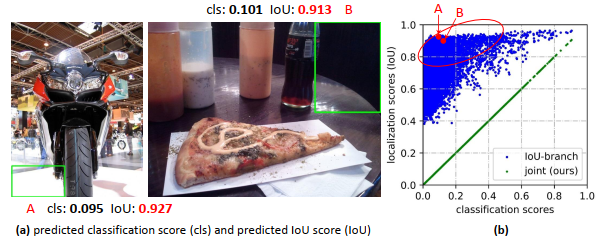
上图（a）表示现有工作训练时单独优化质量估计和分类，测试时联合使用，比如下图 (a) 所示，分类分支均给出较低的分数，但是 IOU 分支分数很高，评估时，联合两个分支的分数，分数还是很高。这是因为分类分支能够使得少量的正样本和大量的负样本一起成功训练，但是质量估计通常就只针对正样本训练。

上图 (b) 将分类分支和 IOU 分支联合优化，用 1 个值替换 2 个值，并且训练和测试的结果都是模型直接输出，没有进一步加工。

GFL 随机采样一些样本的分类分支、IOU 分支预测结果，将其绘制到下图 (b) 上，可以看出，在分类分支给出低预测分数时，IOU 分支分数很高，而 GFL 强制将两个值预测为一个值，也就是时刻相等了

（2）Bbox 表示不灵活

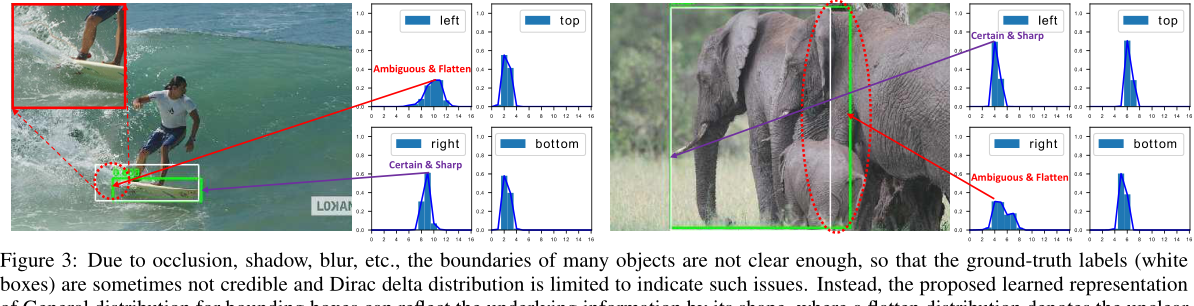
在 FasterRCNN 、MaskRCNN 、FCOS 、ATSS 等框架中，将 Bbox 表示为一个 Dirac delta distribution，并没有考虑到数据的歧义及不确定性，虽然有部分工作将框建模为高斯分布，但是实际情况表现得不是高斯分布一样简单，比如上图，在位置明确位置，其周围的预测概率表现为中间高两边低，和高斯分布接近，但是不明确位置，却表现为双峰现象，这和高斯分布不匹配

Method

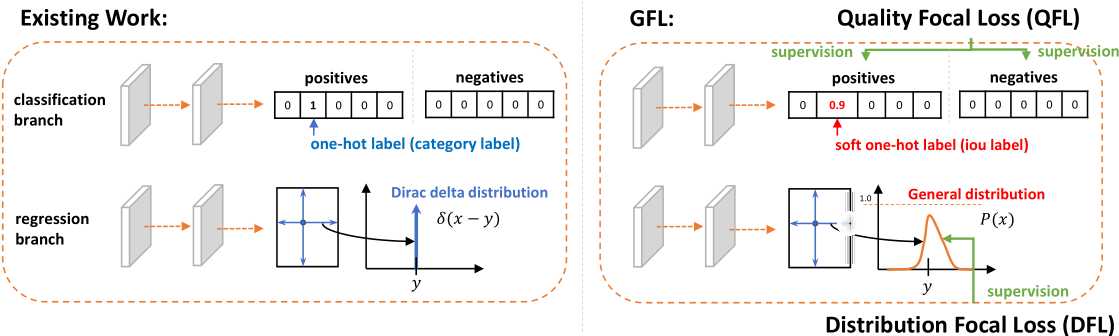
为了解决以上两个问题，GFL 为边界框和定位质量设计新的表示，对于定位质量表示，我们建议将其与分类分数合并为一个统一的表示：一个分类向量，其在真实类别索引处的值指的是其对应的定位质量，在训练时和推理时均是直接使用，消除训练、测试不一致的问题。

对于边界框表示，GFL 直接学习其连续空间上的离散概率分布来表示框位置的任意分布，而不引入任何体验分布，以获得更加可靠准确的边界框估计

1. Focal loss (FL)-> Quality Focal loss (QFL)

Focal loss (FL)：其定义如下，其中 y 是真实标签，pt 是预测概率，$-log(p_t)$ 是交叉熵，$(1-p_t)^\gamma$ 是动态加权，当 $\gamma>1$ 时，预测概率 $p_t$ 越高，样本越容易区分，其权重也就越低，反之，难分样本权重越大

$$\left.\mathbf{FL}(p)=-(1-p_t)^\gamma\log(p_t),p_t=\left\{\begin{array}{ccc}p,&\text{when}&y=1\\1-p,&\text{when}&y=0\end{array}\right.\right.$$

Quality Focal loss (QFL)：为解决训练、测试不一致的问题，将 IOU 分数和分类分数联合表示，此时监督标签改为 one-hot 化的标签，但是在真实标签位置不是填 1，而是填取值在 [0,1] 之间的 IOU 分数，这是通过在类别数量 n 上实现 n 个 sigmoid 实现，并记输出为 $\sigma$

由于分类问题仍然存在类别不平衡问题，这里在 FL 的基础上，设计 IOU - 分类联合分支的损失，但是由于 y 只支持离散取值，GFL 将 FL 的两部分作以下扩展：

• 交叉熵部分写出完整形式：即 $-((1-y)log(1-\sigma)+ylog(\sigma))$
• 动态权重改为 y 与 $\sigma$ 的绝对损失，即 $|y-\sigma|^\beta,(\beta>0)$

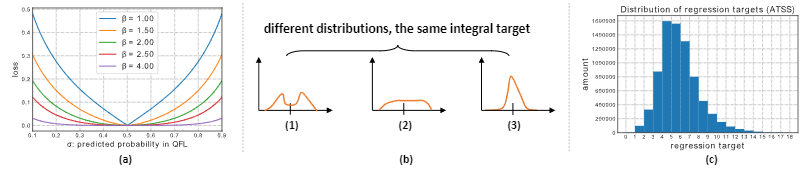
当 $\sigma=y$ 时，QFL 取得最小值，下图 (a) 是 y=0.5 时的 QFL 值，可知其预测值越接近 $\sigma$，其损失越小

2. Distribution Focal Loss (DFL)

如果分布过于任意，网络学习的效率可能会不高，原因是一个积分目标可能对应了无穷多种分布模式。如上图 (b) 所示，GFL 在上图 © 统计 ATSS 在 COCO 上的样本回归统计，发现 (b) 中的 (3) 更符合实际情况，于是增加以下约束：

$$\mathbf{DFL}(\mathcal{S}_i,\mathcal{S}_{i+1})=-\big((y_{i+1}-y)\log(\mathcal{S}_i)+(y-y_i)\log(\mathcal{S}_{i+1})\big).$$

含义：以类似交叉熵的形式去优化与标签 y 最接近的一左一右两个位置的概率，从而让网络快速地聚焦到目标位置的邻近区域的分布中去。标签 y 表示中心点到四周的距离

Generalized Focal loss (GFL)

以上的 QFL 和 DFL 可以看作是 GFL 的特殊形式，GFL 表示为：

$$\mathbf{GFL}(p_{y_{l}},p_{y_{r}})=-\big|y-(y_{l}p_{y_{l}}+y_{r}p_{y_{r}})\big|^{\beta}\big((y_{r}-y)\log(p_{y_{l}})+(y-y_{l})\log(p_{y_{r}})\big).$$

训练 GFL

定义使用 GFL 定义损失，其中 $N_{pos}$ 表示正样本数量，$L_{Q}、L_{D}$ 表示 DFL、DFL，$L_B$ 表示 GIOU loss，$c_z^*$ 是指示函数，大于 0 时取 1，否则为 0

$$\mathcal{L}=\frac{1}{N_{pos}}\sum_{z}\mathcal{L}_{Q}+\frac{1}{N_{pos}}\sum_{z}\mathbf{1}_{\{c_{z}^{*}>0\}}\big(\lambda_{0}\mathcal{L}_{\mathcal{B}}+\lambda_{1}\mathcal{L}_{\mathcal{D}}\big),$$

• 的 uuu
  • 的空间打开

参考：

1. zhuanlan.zhihu.com/p/147691786
2. Site Unreachable