机器学习集成算法通用知识

什么是集成学习 (ensemble)？

• 结合使用给定学习算法构建的几个基本估计器的预测，以提高单个估计器的泛化性 / 鲁棒性
• 多个模型的预测结果的并集。您可以通过以下一项或多项来创建集成学习： 不同的初始化 不同的超参数 不同的整体结构 深度模型和宽度模型属于一种集成学习

介绍流行的集成算法 ？

• 装袋算法 (Bagging)：先将训练集分离成多个子集，然后通过各个子集训练多个模型
• 提升算法 (Boosting)：训练多个模型并组成一个序列，序列中的每一个模型都会修正前一个模型的错误
• 堆叠算法 (Stacking)： 是一种分层模型集成框架。以两层为例，首先将数据集分成训练集和测试集，利用训练集训练得到多个初级学习器，然后用初级学习器对测试集进行预测，并将输出值作为下一阶段训练的输入值，最终的标签作为输出值，用于训练次级学习器

如何从偏差和方差的角度解释 bagging 和 boosting 的原理？

• Bagging 对样本重采样，对每一重采样得到的子样本集训练一个模型，最后取平均。由于子样本集的相似性以及使用的是同种模型，因此各模型有近似相等的方差 (Bias) 和偏差 (Variabce)。由于 E [∑Xin]=E [Xi]，所以 bagging 后的方差 (Bias) 和单个子模型的接近，一般来说不能显著降低方差 (Bias)。另一方面，若各子模型独立，则有 Var [∑Xin]=Var [Xi] n，此时可以显著降低偏差 (Variabce)。若各子模型完全相同，则 Var [∑Xin]=Var [Xi]，此时不会降低偏差 (Variabce)。
• bagging 方法得到的各子模型是有一定相关性的，属于上面两个极端状况的中间态，因此可以一定程度降低偏差 (Variabce)。 boosting 从优化角度来看，是用 forward-stagewise 这种贪心法去最小化损失函数，由于采取的是串行优化的策略，各子模型之间是强相关的，于是子模型之和并不能显著降低偏差 (Variabce)。所以说 boosting 主要还是靠降低方差 (Bias) 来提升预测精度

boosting 和 bagging 的区别？

• 样本选择上
  • Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的
  • Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整
• 样例权重
  • Bagging：使用均匀取样，每个样例的权重相等
  • Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大
• 预测函数
  • Bagging：所有预测函数的权重相等
  • Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重.
• 并行计算
  • Bagging：各个预测函数可以并行生成
  • Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果

请描述随机森林 (Random Forest)、Boosting Tree 和梯度提升树 (Gradient Boosting Decision Tree, GBDT) 之间的区别？

• 随机森林 (RandomForest) 算法 : Bagging + Decision tree
• BoostingTree : AdaBoost + Decision tree
• 梯度提升树 : Gradient Boost + Decision tree
• 相同点：1. 都是由多棵树组成；2. 最终的结果都是由多棵树一起决定
• 不同点：1. 随机森林的子树可以是分类或回归树，而 GBDT 只能是回归树；2. 随机森林可以并行生成，而 GBDT 只能是串行；3. 输出结果，随机森林采用多数投票，GBDT 将所有结果累加起来；4. 随机森林对异常值不敏感，GBDT 敏感；5：随进森林减少方差，GBDT 减少偏差；6：随机森林对数据集一视同仁，GBDT 是基于权值的弱分类器的集成

梯度提升树 (Gradient Boosting Decision Tree, GBDT) 和 XGBoost（eXtreme Gradient Boosting） 区别？

• GBDT 是机器学习算法，XGBoost 是该算法的工程实现
• 在使用 CART 作为基分类器时，XGBoost 显式地加入了正则化 (regularization) 项来控制模型的复杂度，有利于防止过拟合 (overfitting)，从而提高模型的泛化能力
• GBDT 在模型训练时只使用了代价函数的一阶导数信息，XGBoost 对代价函数进行二阶泰勒展开，可以同时使用一阶和二阶导数
• 传统的 GBDT 采用 CART 作为基分类器，XGBoost 支持多种类型的基分类器，比如线性分类器
• 传统的 GBDT 在每轮迭代时使用全部的数据，XGBoost 则采用了与随机森林相似的策略，支持对数据进行采样
• 传统的 GBDT 没有设计对缺失值进行处理，XGBoost 能够自动学习出缺失值的处理策略

LightGBM （Light Gradient Boosting Machine） 比 XGBoost（eXtreme Gradient Boosting） 优势在哪里？

• 在树分裂计算分裂特征的增益时，xgboost 采用了预排序的方法来处理节点分裂，这样计算的分裂点比较精确。但是，也造成了很大的时间开销。
• Lightgbm 选择了基于 histogram 的决策树算法。相比于 pre-sorted 算法，histogram 在内存消耗和计算代价上都有不少优势

梯度提升树 (Gradient Boosting Decision Tree, GBDT) 和随机森林 (Random Forest) 哪个容易过拟合？

• 随机森林，因为随机森林的决策树尝试拟合数据集，有潜在的过拟合 (overfitting) 风险
• boostingd 的 GBDT 的决策树则是拟合数据集的残差，然后更新残差，由新的决策树再去拟合新的残差，虽然慢，但是难以过拟合

集成算法 中学习器结合的策略？

• 平均法（averaging）: 分为简单平均和加权平均， 加权平均法的权重一般从训练数据中学习得到。但由于噪声干扰和过拟合问题，加权平均法也未必优于简单平均法。一般而言，个体学习器性能相差较大时，宜用加权平均法，否则宜用简单平均法
• 投票法（voting）：绝对多数投票法（majority voting）、相对多数投票法（plurality voting）、 加权投票法（weighted voting）
• 学习法： 将个体学习器称为 初级学习器，用于结合的学习器称为 次级学习器，或 元学习器（meta-learner）

描述随机森林中决策树的建立？

• 在建立每一棵决策树的过程中，有两点需要注意：采样与完全分裂
• 首先进行行采样（随机样本）：采用有放回的方式，也就是在采样得到的样本集合中可能有重复的样本。假设输入样本为 N 个，那么采样的样本也为 N 个。这样在训练的时候，每一棵树的输入样本都不是全部的样本，就相对不容易出现过拟合。
• 然后进行列采样（随机特征）：从 M 个 feature 中选出 m 个（m＜＜M）。之后再对采样之后的数据使用完全分裂的方式建立决策树，这样决策树的某一个叶子节点要么是无法继续分裂的，要么所有样本都指向同一个分类
• 一般很多的决策树算法都有一个重要的步骤 —— 剪枝，但是这里不这么做，因为两个随机采样过程保证了随机性，所以不剪枝也不会出现过拟合 (overfitting)

提升方法关键的两个内容是？

• 对提升方法来说，有两个问题需要回答：一是在每一轮如何改变训练数据的权值或概率分布；二是如何将弱分类器组合成一个强分类器
• 关于第 1 个问题，AdaBoost 的做法是，提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值。这样一来，那些没有得到正确分类的数据，由于其权值的加大而受到后一轮的弱分类器的更大关注。于是，分类问题被一系列的弱分类器 “分而治之”
• 至于第 2 个问题，即弱分类器的组合，AdaBoost 采取加权多数表决的方法。具体地，加大分类误差率小的弱分类器的权值，使其在表决中起较大的作用，减小分类误差率大的弱分类器的权值，使其在表决中起较小的作用

什么是投票算法（Voting）？

• 投票算法（Voting）是通过创建两个或多个算法模型，利用投票算法将这些算法包装起来，计算各个子模型的平均预测状况。
• 在实际的应用中，可以对每个子模型的预测结果增加权重，以提高算法的准确度。但是，在 scikit-learn 中不提供加权算法

什么是提升方法？

• 对于分类问题而言，给定一个训练样本集，求比较粗糙的分类规则（弱分类器）要比求精确的分类规则（强分类器）容易得多。
• 提升方法就是从弱学习算法出发，反复学习，得到一系列弱分类器（又称为基本分类器），然后组合这些弱分类器，构成一个强分类器。
• 大多数的提升方法都是改变训练数据的概率分布（训练数据的权值分布），针对不同的训练数据分布调用弱学习算法学习一系列弱分类器
• 常见的用于机器学习的提升算法：AdaBoost

什么是极端随机树？

• 与随机森林 (Random Forest) 十分相似，都是由许多决策树构成
• 随机森林 (Random Forest) 应用的是 Bagging 模型，而极端随机树是使用所有的训练样本得到每棵决策树，也就是每棵决策树应用的是相同的全部训练样本。
• 随机森林 (Random Forest) 是在一个随机子集内得到最优分叉特征属性，而极端随机树是完全随机地选择分叉特征属性，从而实现对决策树进行分叉的

什么是随机梯度提升法（GBM）？

• 要找到某个函数的最大值，最好的办法就是沿着该函数的梯度方向探寻。梯度算子总是指向函数值增长最快的方向
• 由于梯度提升算法在每次更新数据集时都需要遍历整个数据集，计算复杂度较高，于是有了一个改进算法 —— 随机梯度提升算法，该算法一次只用一个样本点来更新回归系数，极大地改善了算法的计算复杂度

什么是投票分类器？

• 投票分类器（VotingClassifier）背后的想法是结合概念上不同的机器学习分类器，并使用多数票或平均预测概率（软投票）来预测类标签。这样的分类器对于一组表现同样好的模型来说是很有用的，以平衡它们各自的弱点

 >>> from sklearn import datasets
 >>> from sklearn.tree import DecisionTreeClassifier
 >>> from sklearn.neighbors import KNeighborsClassifier
 >>> from sklearn.svm import SVC
 >>> from itertools import product
 >>> from sklearn.ensemble import VotingClassifier


 >>> # Loading some example data
 >>> iris = datasets.load_iris()
 >>> X = iris.data[:, [0, 2]]
 >>> y = iris.target

 >>> # Training classifiers
 >>> clf1 = DecisionTreeClassifier(max_depth=4)
 >>> clf2 = KNeighborsClassifier(n_neighbors=7)
 >>> clf3 = SVC(kernel='rbf', probability=True)
 >>> eclf = VotingClassifier(estimators=[('dt', clf1), ('knn', clf2), ('svc', clf3)],
...                         voting='soft', weights=[2, 1, 2])

 >>> clf1 = clf1.fit(X, y)
 >>> clf2 = clf2.fit(X, y)
 >>> clf3 = clf3.fit(X, y)
 >>> eclf = eclf.fit(X, y) 

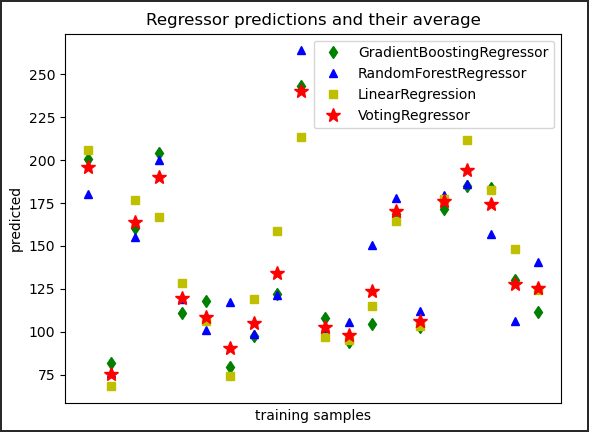
什么是投票回归器？

• VotingRegressor 背后的想法是结合概念上不同的机器学习回归器，并返回平均预测值。这样的回归器对于一组表现同样好的模型来说是有用的，以平衡它们各自的弱点

>>> from sklearn.datasets import load_diabetes
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import RandomForestRegressor
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.ensemble import VotingRegressor


>>> # Loading some example data
>>> X, y = load_diabetes(return_X_y=True)

>>> # Training classifiers
>>> reg1 = GradientBoostingRegressor(random_state=1)
>>> reg2 = RandomForestRegressor(random_state=1)
>>> reg3 = LinearRegression()
>>> ereg = VotingRegressor(estimators=[('gb', reg1), ('rf', reg2), ('lr', reg3)])
>>> ereg = ereg.fit(X, y)