A survey of loss functions for semantic segmentation

发表于 更新于 分类于 ， ， ， 阅读次数： 本文字数： 3.5k 阅读时长 ≈ 3 分钟

将 15 种语义分割函数分为 4 类进行归纳总结，并提出 Log-Cosh Dice Loss 损失

  • 语义分割目前有哪些损失函数？

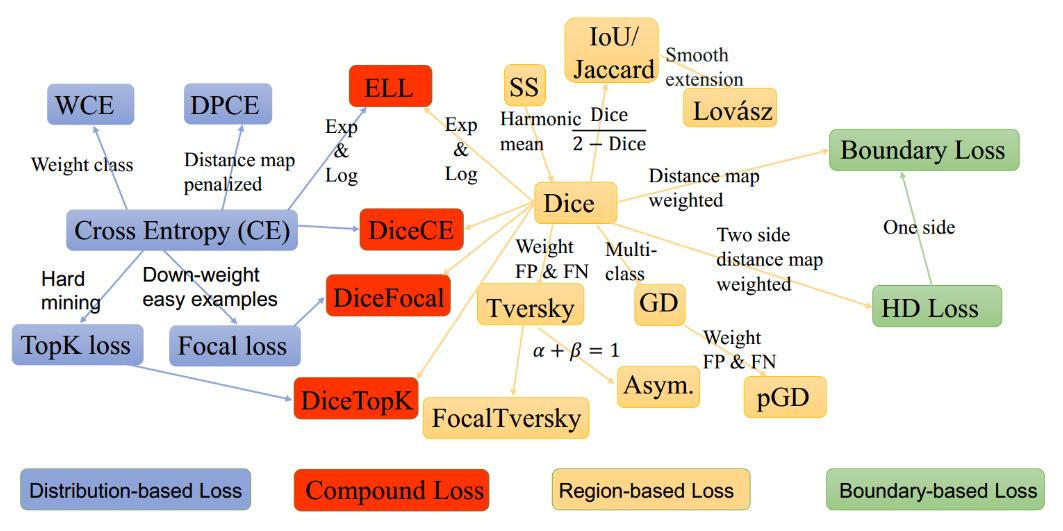
    • 基于分布 (Distribution-based)：基于模型输出概率分布和 gt 分布差异，计算损失，以交差熵为代表
    • 基于区域 (Region-based)：基于模型输出区域与 gt 区域计算损失，以 Dice 为代表
    • 基于边界 (Boundary-based)：考虑形状
    • 基于复合 (Compounded)：组合两种以上的损失函数，如 CE+Dice

  • 什么是加权的二值交叉熵损失 (Weighted Binary Cross-Entropy, WCE)?

    • 在交叉嫡 Loss 的基础上为每一个类别添加了一个权重参数为正样本加权。设置 β>1\beta >1, 减少假阴性；设置 β<1\beta <1, 减少假阳性。这样相比于原始的交叉嫡 Loss, 在样本数量不均衡的情况下可以获得更好的效果

    WCE(p,p^)=−(βplog⁡(p^)+(1−p)log⁡(1−p^))\text{WCE}(p,\hat{p})=-(\beta p\log(\hat{p})+(1-p)\log(1-\hat{p}))

  • 什么是平衡交差熵损失 (Balanced Cross-Entropy, BCE)?

    • 与加权交叉熵损失函数类似，但平衡交叉熵损失函数对负样本也进行加权

    BCE(p,p^)=−(βplog⁡(p^)+(1−β)(1−p)log⁡(1−p^))\text{BCE}(p,\hat{p})=-(\beta p\log(\hat{p})+(1-\beta)(1-p)\log(1-\hat{p}))

  • 什么是距离图得出的损失惩罚项 (Distance map derived loss penalty term)?

    • 将距离图定义为 ground truth 与预测图之间的距离（欧几里得距离、绝对距离等）
    • 合并映射的方法有 2 种，一种是创建神经网络架构，在该算法中有一个用于分割的重建 head，或者将其引入损失函数。遵循相同的理论，可以从 GT mask 得出的距离图，并创建了一个基于惩罚的自定义损失函数。使用这种方法，可以很容易地将网络引导到难以分割的边界区域

  • 什么是 Tversky Loss？

    • Tversky 系数是 Dice 系数和 Jaccard 系数的一种推广。当设置 α\alpha = β\beta =0.5, 此时 Tversky 系数就是 Dice 系数。而当设置 α\alpha = β\beta =1 时，此时 Tversky 系数就是 Jaccard 系数。α\alpha 和 β\beta 分别控制假阴性和假阳性。通过调整 α\alpha 和 β\beta, 可以控制假阳性和假阴性之间的平衡

    T(A,B)=∣A∩B∣∣A⋂B∣+α∣A−B∣+β∣B−A∣TL(p,p^)=1−1+pp^1+pp^+β(1−p)p^+(1−β)p(1−p^)\begin{aligned}T(A,B)=\frac{|A\cap B|}{|A\bigcap B|+\alpha|A-B|+\beta|B-A|} \\ TL(p,\hat{p})=1-\frac{1+p\hat{p}}{1+p\hat{p}+\beta(1-p)\hat{p}+(1-\beta)p(1-\hat{p})}\end{aligned}

  • 什么是 Focal Tversky Loss？

    • “Focal loss” 相似，后者着重于通过降低易用 / 常见损失的权重来说明困难的例子。Focal Tversky Loss 还尝试借助 γ 系数来学习诸如在 ROI（感兴趣区域）较小的情况下的困难示例

    FTL=∑c(1−TIc)γFTL=\sum_c\left(1-TI_c\right)^{\gamma}

  • 什么是 Sensitivity Specificity Loss？

    • 与 Dice 系数相似，灵敏度和特异性是评价分割预测的常用指标。在这个损失函数中，我们可以用参数来解决类不平衡问题

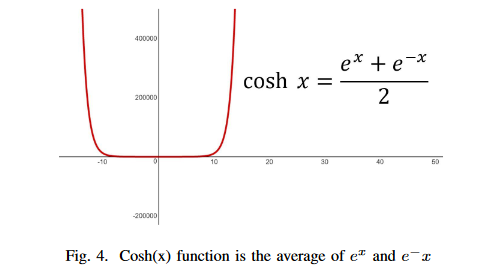
  • 什么是 Log-Cosh Dice Loss？

    • 将 Cosh (x) 函数和 Log (x) 函数合并，可以得到 Log-Cosh Dice Loss

    Llc−dce=log⁡(cosh⁡(DiceLoss⁡))L_{lc-dce}=\log(\cosh(\operatorname{DiceLoss}))

  • 什么是 Shape-aware Loss？

    • 顾名思义考虑了形状。通常所有损失函数都在像素级起作用，Shape-aware Loss 会计算平均点到曲线的欧几里得距离，即预测分割到 ground truth 的曲线周围点之间的欧式距离，并将其用作交叉熵损失函数的系数

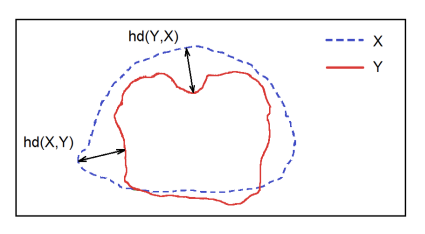
    Ei=D(C^,CGT)Lshape − aware =−∑iCE(y,y^)−∑iEiCE(y,y^)\begin{array}{l}E_i=D\left(\hat C,C_{GT}\right)\\ L_{\mathrm{shape~}-\mathrm{~aware~}}=-\sum_i C E(y,\hat y)-\sum i E_i C E(y,\hat y)\end{array}

  • 什么是 Hausdorff Distance Loss？

    • Hausdorff Distance Loss（HD）是分割方法用来跟踪模型性能的度量

    d(X,Y)=max⁡xϵXmin⁡yϵY∥x−y∥2d(X,Y)=\max\limits_{x\epsilon X}\min\limits_{y\epsilon Y}\|x-y\|_2

  • 什么是 Exponential Logarithmic Loss？

    • 指数对数损失函数集中于使用骰子损失和交叉熵损失的组合公式来预测不那么精确的结构。对骰子损失和熵损失进行指数和对数转换，以合并更精细的分割边界和准确的数据分布的好处

    LExp=wDiceLDice+wcrossLcrossLDice=E(−ln⁡(DC)γDie)Lcross=E(wl(−ln⁡(pl)γcross))\begin{array}{ll}L_{Exp}=w_{\mathrm{Dice}}L_{\mathrm{Dice}}+w_{\mathrm{cross}}L_{\mathrm{cross}}\\ L_{\mathrm{Dice}}=E\left(-\ln(DC)^{\gamma_{\mathrm{Die}}}\right)\\L_{\mathrm{cross}}=E\left(w_l(-\ln(p_l)^{\gamma_{\mathrm{cross}}})\right)\end{array}

  • 什么是 Combo Loss？

    • 组合损失定义为 Dice loss 和修正的交叉嫡的加权和。它试图利用 Dice 损失解决类不平衡问题的灵活性，同时使用交叉嫡进行曲线平滑

    Lm−bec=−1N∑iβ(y−log⁡(y^))+(1−β)(1−y)log⁡(1−y^)CL(y,y^)=αLm−bce−(1−α)DL(y,y^)\begin{array}{l}L_{m-bec}=-\dfrac{1}{N}\sum_i\beta(y-\log(\hat{y}))+(1-\beta)(1-y)\log(1-\hat{y})\\ CL(y,\hat{y})=\alpha L_{m-bce}-(1-\alpha)DL(y,\hat{y})\end{array}

参考：

  1. 图像分割模型调优技巧，loss 函数大盘点 - 知乎