ResNet:Deep Residual Learning for Image Recognition
通过网络的跳跃连接实现残差学习 ,使得神经网络可以无需考虑梯度消失或梯度爆炸即可搭建深层网络
什么是 ResNet?
![ResNet-20230408140940]()
- 通过网络的跳跃连接实现残差学习 ,使得神经网络可以无需考虑梯度消失或梯度爆炸即可搭建深层网络,相较于 VGGNet 的 19 层和 GoogleNetv1 的 22 层,ResNet 可以提供 18、34、50、101、152 甚至更多层的网络,同时获得更好的精度
- 值得注意的是,残差网络虽然解决加深网络带来的梯度消失、梯度爆炸或网络退化的问题,但是却不是整个网络起的作用,而是某些更短的关键层整体起的作用,和集成算法 理念相近,和丢弃正则化 (Dropout) 类似
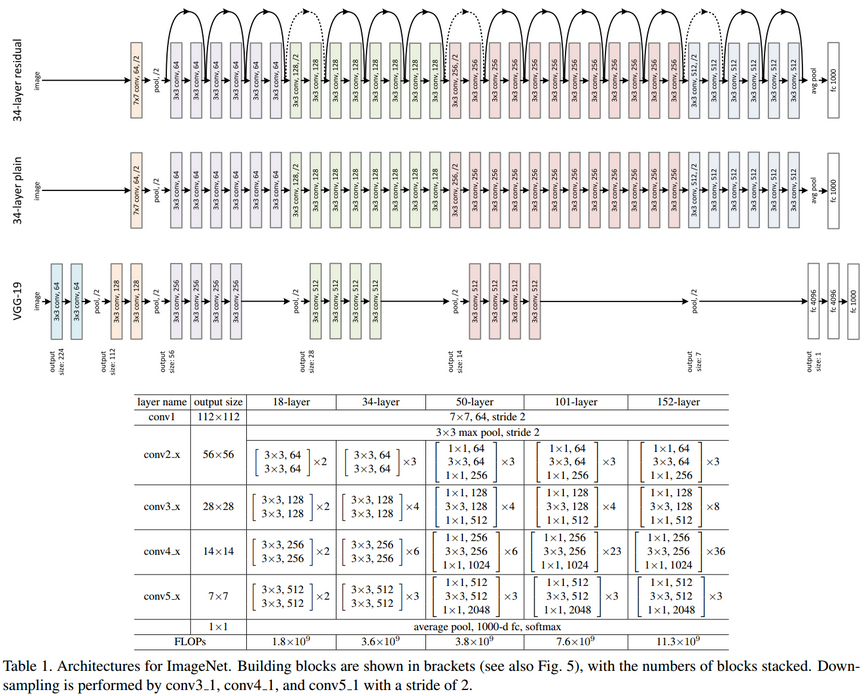
ResNet 的网络结构?
![]()
- 与 plain net 相比,ResNet 多了很多 “旁路”,即 shortcut 路径,其首尾圈出的 layers 构成一个 Residual Block
- ResNet 中,所有的 Residual Block 都没有 pooling 层,降采样是通过 conv 的 stride 实现的
- 分别在 conv3_1、conv4_1 和 conv5_1 Residual Block,降采样 1 倍,同时 feature map 数量增加 1 倍,如图中虚线划定的 block
- 通过 Average Pooling 得到最终的特征,而不是通过全连接层
- 每个卷积层之后都紧接着 BatchNorm layer
简单地堆叠网络会导致什么问题?
![ResNet-20230408140941]()
- 单纯加深网络,并没有带来性能的提升,反而可能出现梯度消失 (gradient vanishing) 、梯度爆炸 (gradient exploding) 和网络退化
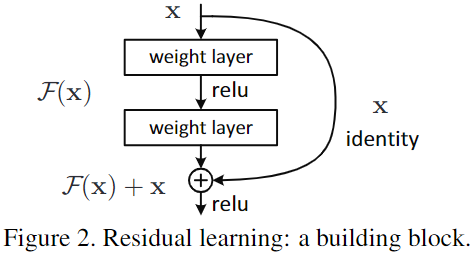
ResNet 如何实现残差学习?
![ResNet-20230408140942]()
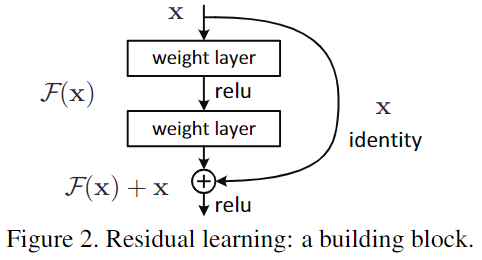
- 又称恒等映射学习,通过在网络上增加跳跃连接 实现恒等映射的学习
- 恒等映射学习表达式如下,其中 x 为输入,F 为神经网络的变换,y 为神经网络的输出
- 神经网络学习恒等映射只需要将 ⇒0,而不是 y⇒x,经过验证,网络学习⇒0 比 y⇒更简单、更快
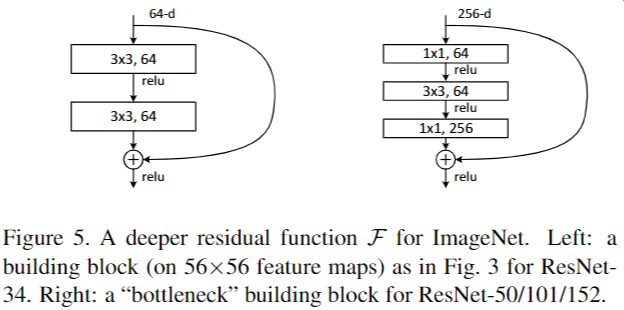
ResNet 如何定义残差块 (residual block)、残差路径、Bottleneck 结构?
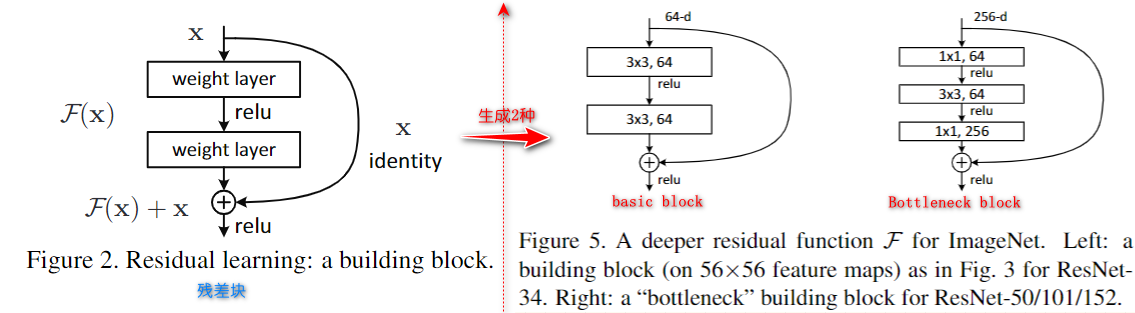
![ResNet-20230408140943]()
残差块: 有 2 个路径,其中 路径是残差路径, 路径为恒等映射,称之为 shortcut 路径,图中的 + 号表示 element-wise addition,要求参与运算的 F (x) 和 x 的尺寸要相同
残差路径: 根据残差块定义,衍生分成 2 种结构,(1)“basic block”,由 2 个 3×3 卷积层构成;(2)Bottleneck,由 1×1 卷积构造,相比较 “basic block” 结构可降低计算复杂度的现实考虑
1
2
3
4
5
6
7
8
9
10
11class Bottleneck(nn.Module):
# Standard bottleneck
def __init__(self, c1, c2, shortcut=True, g=1, e=0.5): # ch_in, ch_out, shortcut, groups, expansion
super(Bottleneck, self).__init__()
c_ = int(c2 * e) # e为缩小因子,表示中间层通道相对输出层减小的比例
self.cv1 = Conv(c1, c_, k=1)
self.cv2 = Conv(c_, c2, k=3, p=1, g=g)
self.add = shortcut and c1 == c2
def forward(self, x):
return x + self.cv2(self.cv1(x)) if self.add else self.cv2(self.cv1(x))
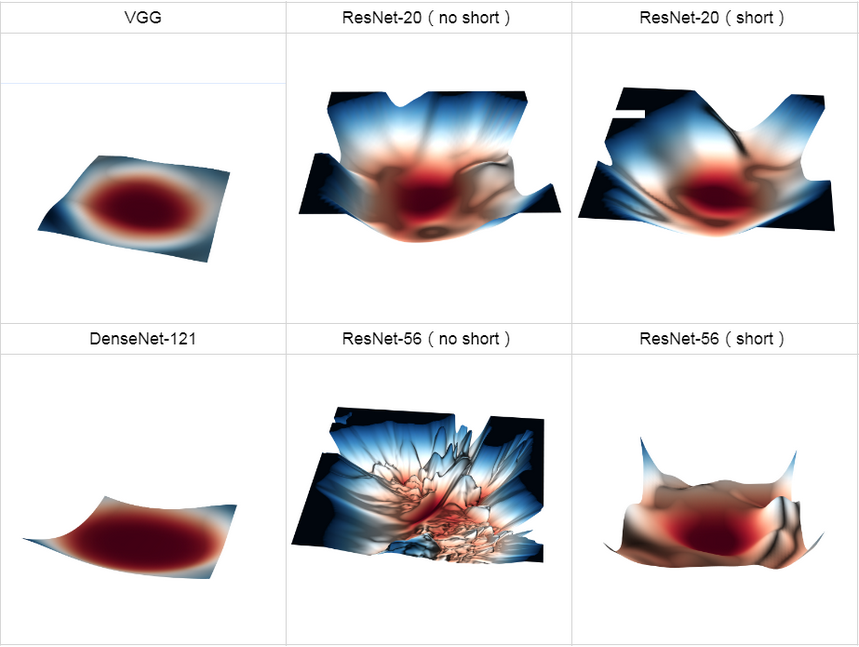
ResNet 改变网络结构,相当于改变网络的 error surface?
![]()
由 [[VGG]] 可知,层数少的网络 error surface 比较简单,以至于 ResNet-20 是否加短连接,对 error surface 影响不大
到 ResNet-56 时,不加短连接网络的 error surface 迅速恶化,变得难以优化,引入 shortcut 后,情况改善
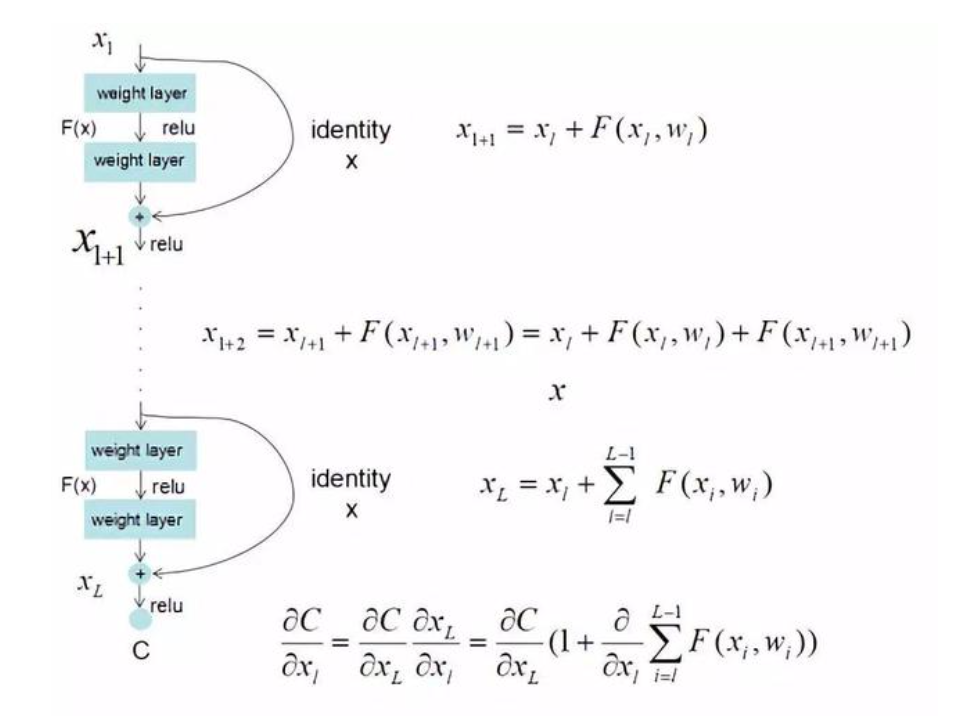
ResNet 为什么可以解决梯度消失?
![]()
- 由于 h (x)=F (x)+x,使得链式求导后的结果如图所示,不管括号内右边部分的求导参数有多小,因为左边的 1 的存在,并且将原来的链式求导中的连乘变成了连加状态,都能保证该节点参数更新不会发生梯度消失或梯度爆炸现象
- ResNet 虽然解决了梯度消失或梯度爆炸,但是本质是解决梯度破碎
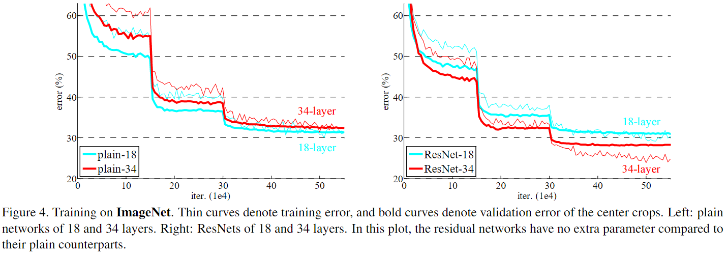
ResNet 为什么可以缓解网络退化?
![ResNet-20230408141028]()
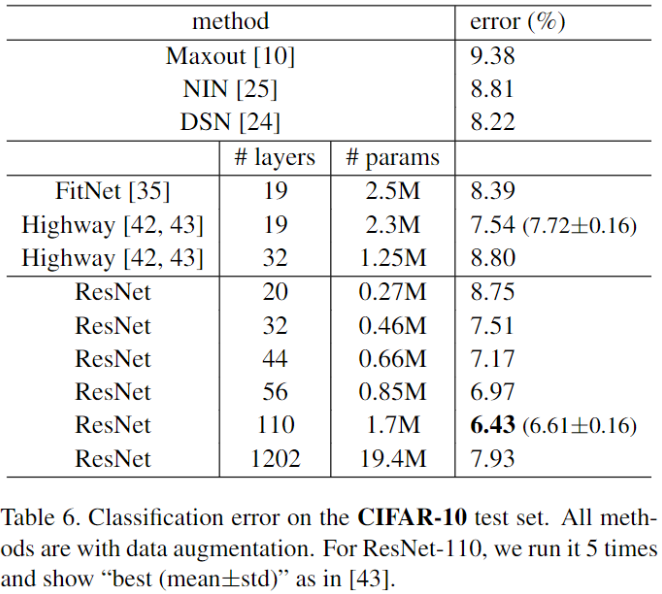
- 左图 18 层网络解空间是 34 层的子空间,但 34 层平面网络在整个训练过程中具有较高的训练误差,出现退化现象,即使添加 BN,确保每层信号不消失,也是这种现象,说明网络退化不是梯度消失或梯度爆炸造成的
- 右图 34 层 ResNet 比 18 层 ResNet 好(2.8%)。更重要的是,34 层 ResNet 显示出相当低的训练误差,并可推广到验证数据。这表明退化问题不是过拟合带来的
- 残差网络残差块表示为:h (x)=F (x)+x,通过学习 F (x)⇒0,使得 h (x)=x,进而使得输入信号可以从任意低层直接传播到高层,梯度可以从任意高层传播到底层,这样的恒等映射这很大程度缓解网络退化现象
ResNet 在大于 1000 层之后,训练效果很好,但是测试效果下降了,为什么?
![ResNet-20230408141029]()
- 残差结构还是可以的,但网络层数太高了,而数据集相对于网络层数来说有点小了
- 当层数比较小的时候,残差结构可以很好的缓和退化问题,因为上一层饱和时可以通过残差映射更快的传递给下一层。但是当深度太高时,就算是简化成只有残差传递的话,所以网络还是退化了,即残差网络可以缓和退化问题,并不说解决
什么是恒等映射?
- 对任意集合 A,如果映射 f:A⇒A 定义为 f (a)=a,即规定 A 中每个元素 a 与自身对应,则称 f 为 A 上的恒等映射
- 在神经网络中的意思是:输入经过若干层的变换后,输出与输入一样,没有发生变化,通过跳跃连接实现恒等映射学习
在神经网络中,什么是跳跃连接?
![ResNet-20230408141029-1]()
- 将神经网络的输出连接到后面神经网络上
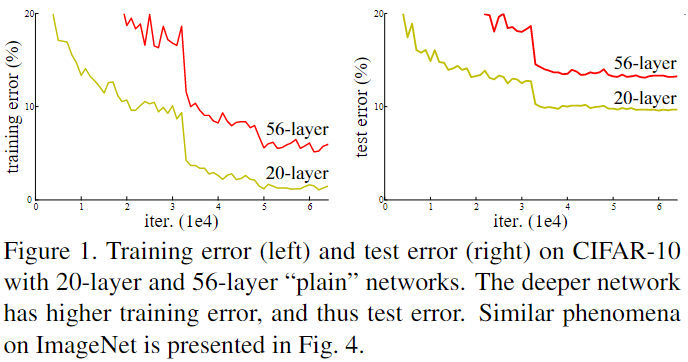
什么是网络退化?
![ResNet-20230408141030]()
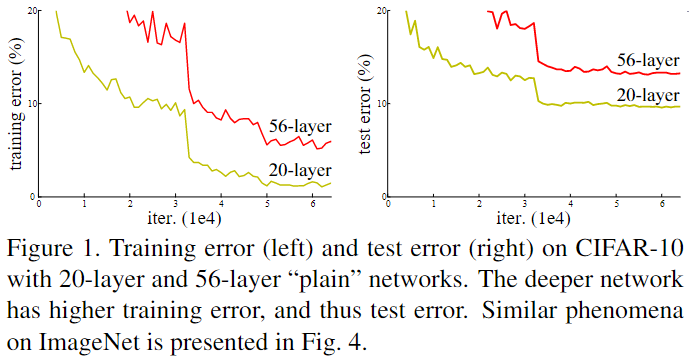
- 网络退化:一般而言,叠加更多的网络层,模型会在训练集及测试集的性能会变好,因为模型复杂度更高了,表达能力更强了,然而实际上却是相反,叠加到一定数量后,网络的学习能力下降了
- 看图可以,训练集及测试集上的 56-layer 效果均比 20layer 差,说明网络退化不是过拟合 (overfitting) 导致的;已知深层神经网络存在梯度消失或梯度爆炸的问题,但是可以通过批规范化 (Batch Normalization,BN) 来缓解这个问题,但是还是出现网络退化问题,既然不是过拟合和梯度消失导致的,那是什么导致的呢?
- 实际上非线性激活函数 Relu 的存在,每次输入到输出的过程都几乎是不可逆的,这也造成了许多 ** 不可逆的信息损失,即冗余层无法学习到恒等映射,** 无法避免出现退化问题
什么是 error surface?
![]()
- 神经网络中 Total Loss 对参数的变化
什么是梯度破碎 (the shattering gradient problem)?
![ResNet-20230408141031]()
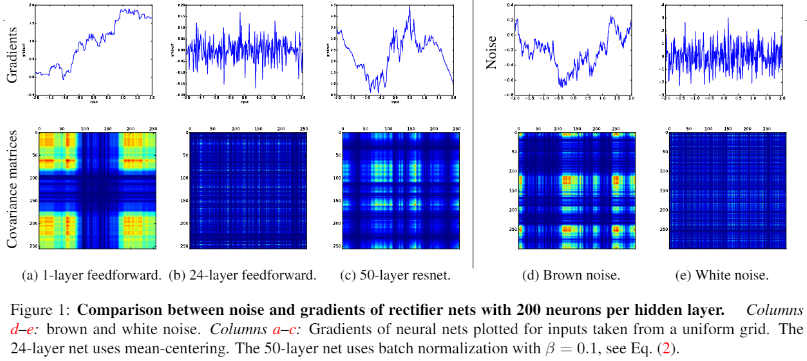
- 在标准前馈神经网络中,随着深度增加,神经元梯度的相关性 (corelation) 按指数级减少 ();同时,梯度的空间结构也随着深度增加被逐渐消除。这也就是梯度破碎现象,上图是神经网络梯度及其协方差矩阵的可视化,可以看到标准的前馈网络的梯度在较深时 (b) 与白噪声 (e) 类似
- 相较标准前馈网络,残差网络中梯度相关性减少的速度从指数级下降到亚线性级 (sublinearly, ),深度残差网络中,神经元梯度介于棕色噪声与白噪声之间 (参见上图中的 c,d,e);残差连接可以极大地保留梯度的空间结构。残差结构缓解了梯度破碎问题
为什么梯度破碎会导致神经网络难以优化?
- 因为许多优化方法假设梯度在相邻点上是相似的,破碎的梯度会大大减小这类优化方法的有效性
- 另外,如果梯度表现得像白噪声,那么某个神经元对网络输出的影响将会很不稳定
为什么 ResNet 网络比普通网络更容易学习?
- 残差网络残差块表示为:h (x)=F (x)+x,通过学习 F (x)⇒0,使得 h (x)=x
- 因为随机初始化权重一般偏向于 0,并且 ReLU 能够将负数激活为 0,过滤了负数的线性变化,所以优化 F (x)⇒0 比 h (x)⇒x 更快
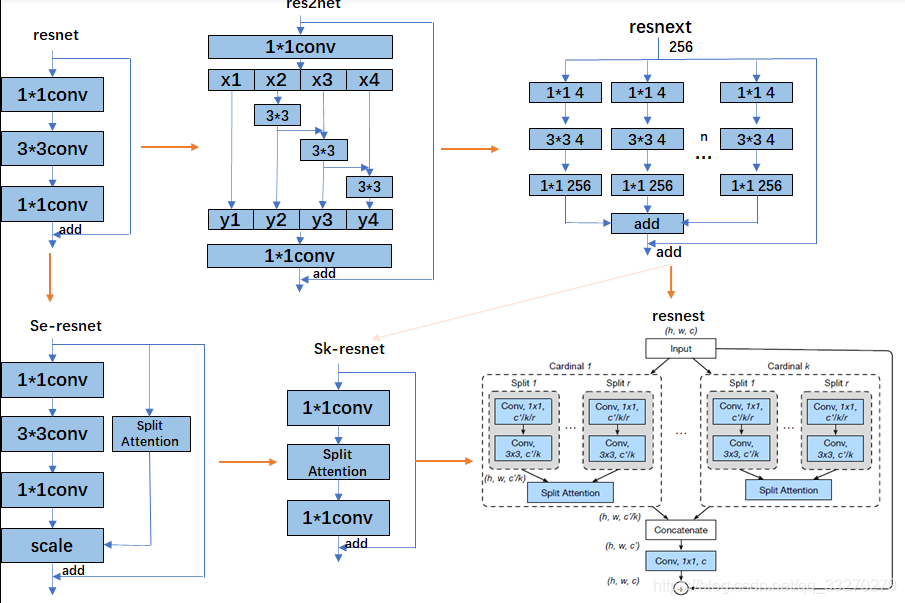
ResNet 系列模型的演化过程?
- ResNet 系列模型主要演化方向包括 2 种:split-transform-merge,squeeze-and-attention
![]()
- split-transform-merge:通过卷积的可分离性质,增加网络宽度,从而在不增加的情况下增加网络的表征能力(不同维度通道特征的融合)
- squeeze-and-attention:核心想法是应用全局上下文预测 channel-wise 的注意力因素