数学上的平均数、调和平均数、几何平均数？

发表于 更新于 分类于 阅读次数： 本文字数： 3.4k 阅读时长 ≈ 3 分钟

本文介绍了一个平时看起来很简单的概念：平均数，但是没想到平均数又可分为算术平均数、调和平均数、几何平均数，乃至最后使用指数平方平均数修正神经网络权重更新过程

什么是算术平均数？

  • 又称均值，是统计学中最基本，最常用的一种平均指标，分为简单算术平均数、加权算术平均数

M=x1+x2+x3+…nM=\frac{x_1+x_2+x_3+…}{n}

什么是调和平均数？

  • 又称倒数平均数，是总体各统计变量倒数的算数平均数的倒数。分为数学调和平均数（数值倒数的平均数的倒数）和统计调和平均数（计算结果与加权算术平均数完全相等）
  • 调和平均数（harmonic mean）：又称倒数平均数，是总体各统计变量倒数 的算术平均数的 倒数

Hn=n∑i=1n1xiH_n=\frac {n} {\sum_{i=1}^{n}\frac{1}{x_i}}

  • 加权调和平均数：是加权算术平均数的变形。它与加权算术平均数在实质上是相同的，而仅有形式上的区别，即表现为变量对称的区别、权数对称的区别和计算位置对称的区别

Hn=∑i=1nmi∑i=1nmixiH_n=\frac {\sum_{i=1}^nm_i} {\sum_{i=1}^{n}\frac{m_i}{x_i}}

什么是几何平均数？

  • 几何平均数是对各变量值的连乘积开项数次方根。根据所拿掌握资料的形式不同，其分为简单几何平均数和加权几何平均数两种形式
  • 简单几何平均

G=nx1∗x2∗x3∗…G=^n\sqrt{x_1*x_2*x_3*…}

  • 加权几何平均

Gn=∑i=1nf∏iNXifiG_n=\sum_{i=1}^n{^f\sqrt{\prod_{i}^NX_i^{f_i}}}

调和平均数与算术平均数的区别？

  • 算术平均数和调和平均数是平均指标的两种表现形式
  • 算术平均数和调和平均数并非两类独立的平均数
  • 算术平均数和调和平均数的数值之间并无直接关系，也不存在谁大谁小的问题；不能根据同一资料既计算算术平均数，又计算调和平均数，否则就是纯数字游戏，而非统计研究

算术平均数、调和平均数、几何平均数的关系？

  • 三种不同形式的平均数，分别有各自的应用条件
  • 进行统计研究时，适宜采用算术平均数时就不能用调和平均数或几何平均数，适宜用调和平均数时，同样也不能采用其他两种平均数
  • 调和平均数 < = 几何平均数 < = 算术平均数 < = 平方平均数

调和值的应用？

  • 考虑一次去便利店并返回的行程 :（1） 去程 速度为 30m/s， 返程 时交通有一些拥堵，所以速度为 10m/s;(3) 去程和返程走的是同一路线，也就是说距离一样（3000 米）；（4） 整个行程的平均速度是多少？

  • 如果不假思索地应用算术平均数的话，结果是 20 mph（(30+10)/2）

  • 但是这么算不对。因为去程速度更快，所以你更快地完成了去程的 5 英里，整个行程中以 30 mph 的速度行驶的时间更少，以 10 mph 的速度行驶的时间更多，所以整个行程期间你的平均速度不会是 30 与 10 的中点，而应该接近 10

  • 加权算术平均数

    1
    2
    3
    4
    去程耗时：3000/30=100 s
    返程耗时：3000/10=300 s
    总耗时：100+300=400s
    算术加权平均数：(30*100/400)+(10*300/400)=15 m/s

  • 调和平均数

    1
    2 / (1/30 + 1/10) = 15 m/s

调和平均数的特点？

  • 调和平均数易受极端值的影响，且受极小值的影响比受极大值的影响更大
  • 只要有一个标志值为 0，就不能计算调和平均数
  • 当组距数列有开口组时，其组中值即使按相邻组距计算，假定性也很大，这时的调和平均数的代表性很不可靠
  • 调和平均数应用的范围较小。在实际中，往往由于缺乏总体单位数的资料而不能直接计算算术平均数，这时需用调和平均法来求得平均数

使用调和平均数的注意事项？

  • 当变量数列有一变量 X 的值为零时，调和平均数公式的分母将等于无穷大，因而无法求出确定的平均值。
  • 调和平均数和算术平均数一样，易受两极端值影响。上端值越大，平均数向上偏离集中趋势就越大。反之，下端值越大，平均数向下偏离集中趋势越大。

什么是指数加权平均 (exponentially weighted averges)？

  • 又称指数移动平均，通过它可以来计算局部的平均值，来描述数值的变化趋势
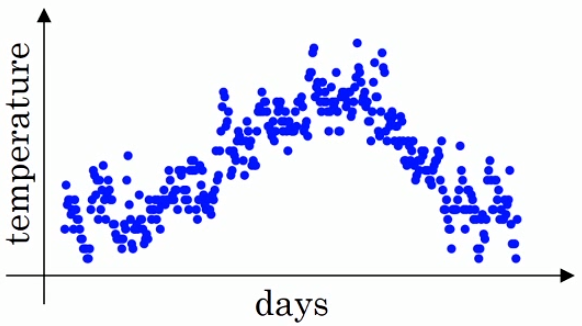
  • 下图是一个天与温度的变化关系，其中横轴表示的是一年中的第几天，纵轴表示的是该天的温度，1 月份和 12 月份的温度相对于年中 (6 月、7 月) 的温度要低一些
  • 通过温度的局部平均值 (移动平均值) 来描述温度的变化趋势，通过下面的公式来计算平均值，θ\theta 表示当天的温度，V\mathrm{V} 表示局部平均值

vt=β∗vt−1+(1−β)∗θtv0=0v1=0.9∗v0+0.1∗θ1v2=0.9∗v1+0.1∗θ2\begin{array}{ll} v_{t}=\beta * v_{t-1}+(1-\beta) * \theta_{t} \\ v_{0}=0 \\ v_{1}=0.9 * v_{0}+0.1 * \theta_{1} \\ v_{2}=0.9 * v_{1}+0.1 * \theta_{2} \end{array}

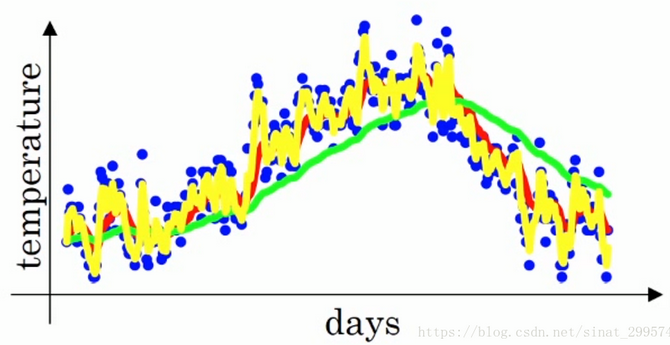
  • 在计算局部温度平均值时，分别取 β=0.9 (红线)，0.98 (绿线)，0.5 (黄线)
  • 其中红线表示 β 为 0.9 时候的温度的加权平均值，绿线表示 β 为 0.98 时候的温度加权平均值，绿线相对于红线来说，更加平稳、稳定。相对于红线来说缺点就是，它向右平移了，产生了延迟，因为当 β 为 0.98 时，相当于平均了 1/(1-0.98)=50 天的温度，而 β 为 0.9 只是平均了 10 天的温度；当 β 为 0.5 时的加权温度平均，相对于红线来说，它抖动的更加厉害，因为它只平均了 2 天的温度，所以对于温度的趋势反馈能够更加的及时，更快的适应温度的变化，同时它也会带来更多的噪声 (平均的天数太少)
  • 如果你想要计算 10 天局部温度的平均值，你需要保存最近 10 的温度。而使用指数加权平均来计算局部平均值的时候，可以节省大量的空间，你只需要保存前一个加权平均值

什么是指数移动平均 (exponentially weighted averges) 的偏差修正？

  • 偏差修正的主要目的是为了提指数加权平均 (exponentially weighted averges) 的精确度，主要是针对前期的加权平均值的计算精度
  • 当 θ0=40,θ1=50\theta_{0}=40, \theta_{1}=50 , 令 β=0.9\beta=0.9, 下面计算加权平均值

v0=0v1=0.9∗v0+0.1∗θ1=0.9∗0+0.1∗40=4v2=0.9∗v1+0.1∗θ2=0.9∗0.1∗θ1+0.1∗θ2=7.1\begin{array}{l} v_{0}=0 \\ v_{1}=0.9 * v_{0}+0.1 * \theta_{1}=0.9 * 0+0.1 * 40=4 \\ v_{2}=0.9 * v_{1}+0.1 * \theta_{2}=0.9 * 0.1 * \theta_{1}+0.1 * \theta_{2}=7.1 \end{array}

  • 通过计算可以发现，前期的指数加权平均存在较大误差，下面通过偏差修正来减少前期指数加权平均的误差，通过将 vtv_{t} 除以 1−βt1-\beta^{t} 来修正指数加权平均的误差，所以更新后的 vt=vt1−βtv_{t}=\frac{v_{t}}{1-\beta^{t}} 随着 t\mathrm{t} 的增大，$ 1-\beta^{t}$ 会趋于 1，因为 $ \beta^{t}会趋0(会趋 0 (\beta <0$) 所以偏差修正对于后期的指数加权平均没有影响
  • 如果你对于前期的局部平均值的精度没有要求，可以不用使用偏差修正，偏差修正主要是针对前期的局部平均值的误差