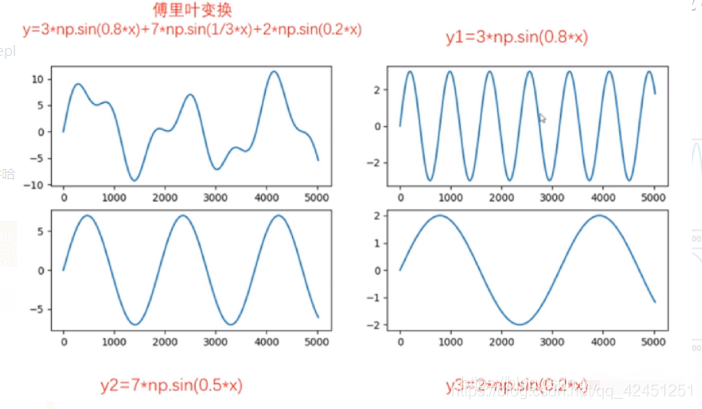
傅里叶变换

发表于 2022-05-16 更新于 2025-01-19 分类于 0-数学基础阅读次数：本文字数： 4.3k 阅读时长 ≈ 4 分钟

本文说明了什么是傅里叶变换，类似泰勒公式，任何公式可以分解为导数组成的若个公式，傅里叶是任何周期性函数可以分解为不同频率的正弦和余弦函数，利用傅里叶变换可以将时域信号变换为频域信号

什么是傅里叶级数？

傅里叶级数公式指出，任何周期函数都可以表示为不同频率的正弦函数和 / 或余弦函数的加权之和，这个和就是傅里叶级数

\begin{aligned}\operatorname{f(t)}&=\operatorname{A}_0+\sum_{n=1}^\infty\operatorname{A}_n\sin(\operatorname{not}+\psi_n)\\ &=\operatorname{A}_0+\sum_{n=1}^\infty[\operatorname{a}_n\cos(\operatorname{not})+\operatorname{b}_n\sin(\operatorname{not})]\end{aligned}

什么是傅里叶变换与傅里叶逆变换？

借鉴傅里叶级数：任何非周期函数也可以表示为不同频率的正弦函数和 / 或余弦函数乘以加权函数的积分，公式 1 是傅里叶变换，公式 2 是傅里叶逆变换

\begin{aligned}\operatorname{f(t)}&=\operatorname{A}_0+\sum_{n=1}^\infty\operatorname{A}_n\sin(\operatorname{not}+\psi_n)\\ &=\operatorname{A}_0+\sum_{n=1}^\infty[\operatorname{a}_n\cos(\operatorname{not})+\operatorname{b}_n\sin(\operatorname{not})]\end{aligned}

傅里叶变换用于分析非周期函数，其实质是将一个信号分离为无穷多多正弦 / 复指数信号的加成，也就是说，把信号变成任意个正弦信号相加的形式。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换
傅里叶变换存在的充分条件是：f (t) 的绝对值的积分是有限的，在信号处理、图像处理领域这一条件都能满足

傅里叶变换的作用？

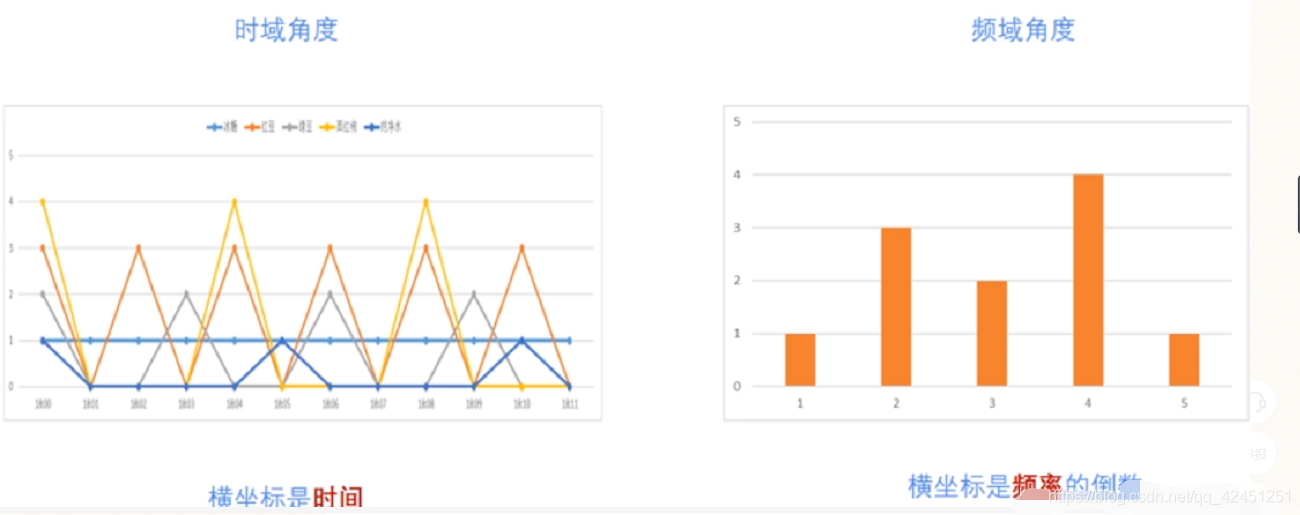
傅里叶变换可以将一个时域信号转换成在不同频率下对应的振幅及相位，其频谱就是时域信号在频域下的表现，而反傅里叶变换可以将频谱再转换回时域的信号
最简单最直接的应用就是时频域转换。将图像时域处理上面复杂的特征转为频域实现简单化，对简单化的特征进行处理，然后再通过傅里叶逆变换回到原来的图像

求解连续非周期信号的傅里叶系数

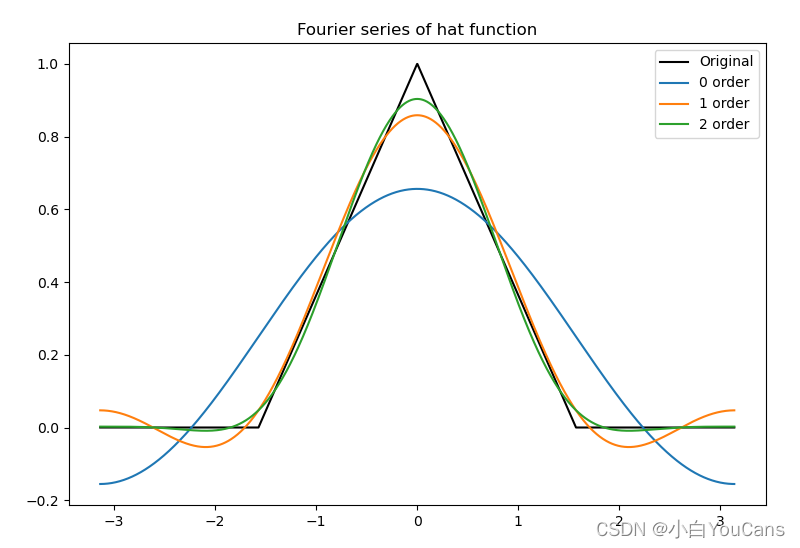
已知 Original 的信号变化过程，如何求该信号的傅里叶系数

设定不同的阶数去求解傅里叶系数，阶数越高，越容易拟合出傅里叶系数

dx = 0.001
x = np.pi * np.arange(-1+dx, 1+dx, dx)
n = len(x)
nquart = int(np.floor(n/4))
# 绘制Original曲线
f = np.zeros_like(x)
f[nquart: 2*nquart] = (4/n) * np.arange(1, nquart+1)
f[2*nquart: 3*nquart] = np.ones(nquart) - (4/n) * np.arange(0, nquart)
plt.figure(figsize=(9, 6))
plt.title("Fourier series of hat function")
plt.plot(x, f, '-', color='k',label="Original")
# 计算傅里叶系数
A0 = np.sum(f * np.ones_like(x)) * dx
fFS = A0 / 2
orders = 3 // 阶数
A = np.zeros(orders)
B = np.zeros(orders)
for k in range(orders):
	A[k] = np.sum(f * np.cos((k+1) * x)) * dx  # Inner product
	B[k] = np.sum(f * np.sin((k+1) * x)) * dx
	# 分别给正弦波和余弦波求系数
	fFS = fFS + A[k] * np.cos((k + 1) * x) + B[k] * np.sin((k + 1) * x) 
	plt.plot(x, fFS, '-', label="{} order".format(k))
	print('Line ', k, ': A = ', A[k], ' B = ', B[k], fFS.shape)
plt.legend(loc="upper right")
plt.show()

如何进行一维傅里叶变换？

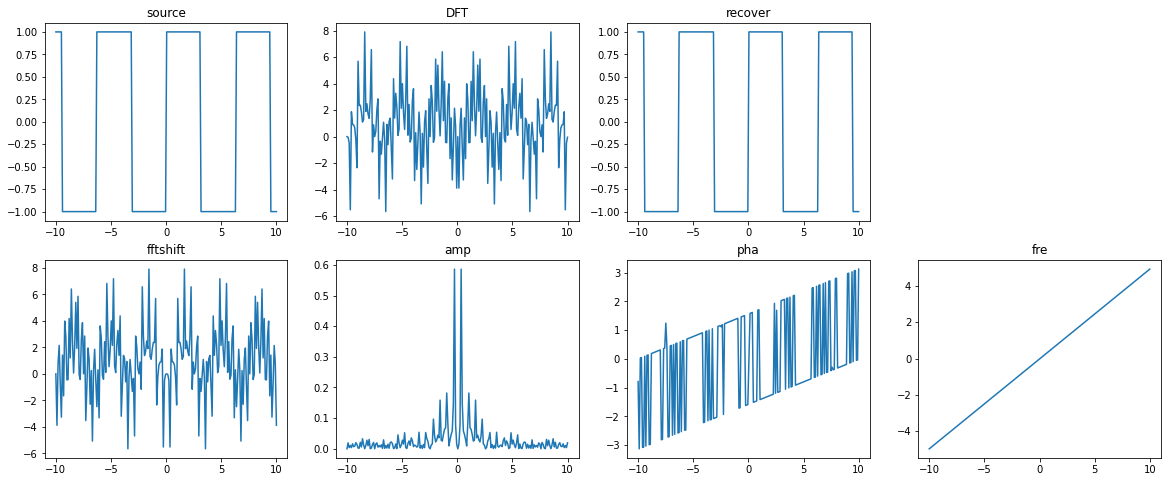
本例使用 numpy 对输入的方波信息进行傅里叶变换，根据变换后的信息还原信号

# 生成方波信号
N = 200
t = np.linspace(-10, 10, N)
dt = t[1] - t[0]
sint = np.sin(t)
sig = np.sign(sint)
plt.plot(t, sig)
# 离散傅里叶变换
fft = np.fft.fft(sig, N)  # 离散傅里叶变换
fftshift = np.fft.fftshift(fft)  # 对称平移
amp = abs(fftshift) / len(fft)  # 幅值
pha = np.angle(fftshift)  # 相位
fre = np.fft.fftshift(np.fft.fftfreq(d=dt, n=N))  # 频率
plt.plot(t, fft)
# 信号恢复
recover = np.zeros(N)
for a, p, f in zip(amp, pha, fre):
	sigCos = a * np.cos(2 * np.pi * f * np.arange(N) * dt + p)  # 根据幅度,相位,频率构造三角函数
	recover += sigCos  # 把这些三角函数都加起来
plt.plot(t, recover)

如何进行二维傅立叶变换？

经过 np.fft.fft2 () 函数实现傅里叶变换得到的图片频谱信息，幅度谱的最大值（低频分量）在左上角 (0,0) 处。为了便于观察，通常用 np.fft.fftshift () 函数将低频分量移动到频域图像的中心位置

normalize = lambda x: (x - x.min()) / (x.max() - x.min() + 1e-6)
imgGray = cv2.imread("../images/Fig0424a.tif", flags=0)  # flags=0 读取为灰度图像
# 傅里叶变换
fft = np.fft.fft2(imgGray)  # np.fft.fft2 实现傅里叶变换
# 非中心化，计算幅度谱和相位谱
ampSpectrum = np.sqrt(np.power(fft.real, 2) + np.power(fft.imag, 2))  # 幅度谱
print("ampSpectrum max={}, min={}".format(ampSpectrum.max(), ampSpectrum.min()))
# phase = np.arctan2(fft.imag, fft.real)  # 计算相位角(弧度制)
# phiSpectrum = phase / np.pi*180  # 将相位角转换为 [-180, 180]
phiSpectrum = np.angle(fft)
# 中心化，将低频分量移动到频域图像的中心
fftShift = np.fft.fftshift(fft)  # 将低频分量移动到频域图像的中心
# 中心化后的幅度谱
ampSpeShift = np.sqrt(np.power(fftShift.real, 2) + np.power(fftShift.imag, 2))
ampShiftNorm = np.uint8(normalize(ampSpeShift)*255)  # 归一化为 [0,255]
# 幅度谱做对数变换
ampSpeLog = np.log(1 + ampSpeShift)  # 幅度谱做对数变换以便于显示
ampSpeLog = np.uint8(normalize(ampSpeLog)*255)  # 归一化为 [0,255]
# np.fft.ifft2 实现图像的逆傅里叶变换
invShift = np.fft.ifftshift(fftShift)  # 将低频逆转换回图像四角
imgIfft = np.fft.ifft2(invShift)  # 逆傅里叶变换，返回值是复数数组
imgRebuild = np.abs(imgIfft)  # 将复数数组调整至灰度空间
show_images([imgGray,phiSpectrum,imgRebuild,ampSpectrum,ampSpeShift,ampSpeLog])

参考：