线性判别分析 LDA

发表于 更新于 分类于 ， 阅读次数： 本文字数： 1.4k 阅读时长 ≈ 1 分钟

什么是线性判别分析（Linear Discriminant Analysis，LDA）？

  • 是一种监督学习的降维技术。其基本思想是将数据投影到一条直线上，使得同类样本的投影点尽可能接近，不同类样本的投影点尽可能远离，从而在新样本分类时，根据其投影点的位置来判断样本的类别。LDA 不同于 PCA（主成分分析），它是一种有监督学习方法，意味着在降维的过程中利用了样本的类别信息
  • 举个通俗易懂的例子，假设我们有两种不同的水果，每种水果有不同的特征（如大小、颜色、形状等）。我们希望建立一个模型，能够根据这些特征来区分两种水果。在这个案例中，我们可以收集两种水果的多个样本，并记录它们的特征。然后使用 LDA 对这些特征进行分析，找到一条最佳的直线（即判别边界），将这两种水果在低维空间中最好地区分开。当我们获得一个新的水果样本时，我们就可以将其投影到这条直线上，根据投影的位置来预测这个水果属于哪一类
  • 基本思想：将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    >>> from sklearn.decomposition import LatentDirichletAllocation
    >>> from sklearn.datasets import make_multilabel_classification
    >>> # This produces a feature matrix of token counts, similar to what
    >>> # CountVectorizer would produce on text.
    >>> X, _ = make_multilabel_classification(random_state=0)
    >>> lda = LatentDirichletAllocation(n_components=5,
        ...     random_state=0)
    >>> lda.fit(X)
        LatentDirichletAllocation(...)
    >>> # get topics for some given samples:
    >>> lda.transform(X[-2:])
        array([[0.00360392, 0.25499205, 0.0036211 , 0.64236448, 0.09541846],
               [0.15297572, 0.00362644, 0.44412786, 0.39568399, 0.003586  ]])

线性判别分析 (LDA) 的思想？

  • 多维空间中，数据处理分类问题较为复杂，LDA 算法将多维空间中的数据投影到一条直线上，将 d 维数据转化成 1 维数据进行处理
  • 对于训练数据，设法将多维数据投影到一条直线上，同类数据的投影点尽可能接近，异类数据点尽可能远离
  • 对数据进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定样本的类别
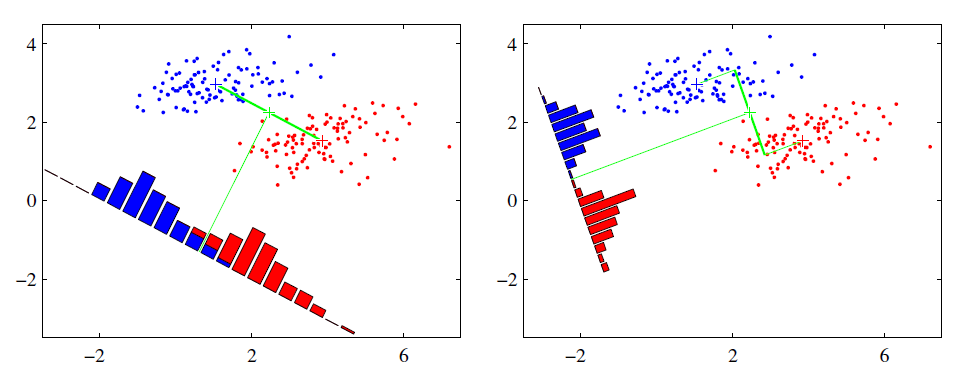
  • 右图红色数据和蓝色数据在各自的区域来说相对集中，根据数据分布直方图也可看出，所以右图的投影效果好于左图，左图中间直方图部分有明显交集