DDPM：Denoising Diffusion Probabilistic Models

发表于 更新于 分类于 ， ， ， 阅读次数： 本文字数： 13k 阅读时长 ≈ 12 分钟

扩散模型包括两个过程，加躁过程通过定义参数计算，不包括学习参数，去躁过程使用 Unet 计算噪声，通过计算加躁前和去躁后的损失，驱动网络训练。无论加躁去躁都是在通过数学证明得到其分布，然后通过 “重参数化” 技术实现采样
(图片)-> 噪声 -> 随机图片，随机图片

什么是 DDPM ？

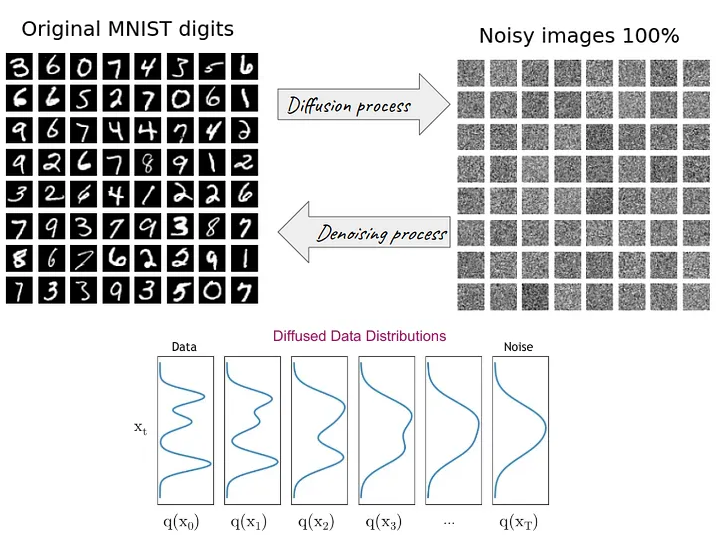
  • DDPM 模型主要分为两个过程：forward 加噪过程（从右往左）和 reverse 去噪过程（从左往右）
  • 加噪过程（Diffusion process）：指向数据集的真实图片中逐步加入高斯噪声，由图片可知，加噪后的数据分布越来越接近高斯分布，也就是变为纯噪声图片
  • 去噪过程（Denoise Process）：指对加了噪声的图片逐步去噪，从而还原出真实图片
  • 加噪过程满足一定的数学规律，而去噪过程则采用神经网络来学习

DDPM 的加躁过程（Diffusion process）？

  • 受到热力学中分子扩散的启发：分子从高浓度区域扩散至低浓度区域，直至整个系统处于平衡，加噪过程也是同理，每次往图片上增加一些噪声，直至图片变为一个纯噪声为止
  • 1）逐步加躁过程：给定初始数据分布 x0∼q(x)x_0\sim q(x) ，然后定义一个扩散过程：逐渐向数据分布添加高斯噪声，共计加噪声 T 次，产生一系列带噪声图片 x1,x2,...,xTx_1, x_2,..., x_T 。在由 xt−1x_{t-1} 到 xtx_t 的过程中，噪声是的标准差 / 方差是以一个在区间 (0,1) 内的固定值 βT\beta_T 确定的，均值是以当前固定值 βT\beta_T 和当前时刻的图片数据 xt−1x_{t-1} 确定。
  • 2）加躁结果：随着 t 的不断增大，原始数据逐步失去他的特征，当 T∼inf⁡T\sim \inf，xTx_T 趋近于一个各向独立的高斯分布。从视觉上来看，就是将原本一张完好的照片加噪很多步后，图片几乎变成了一张完全是噪声的图片，所谓完全噪声，目标与目标、图片与图片的边界都混在一起，无法区分边界
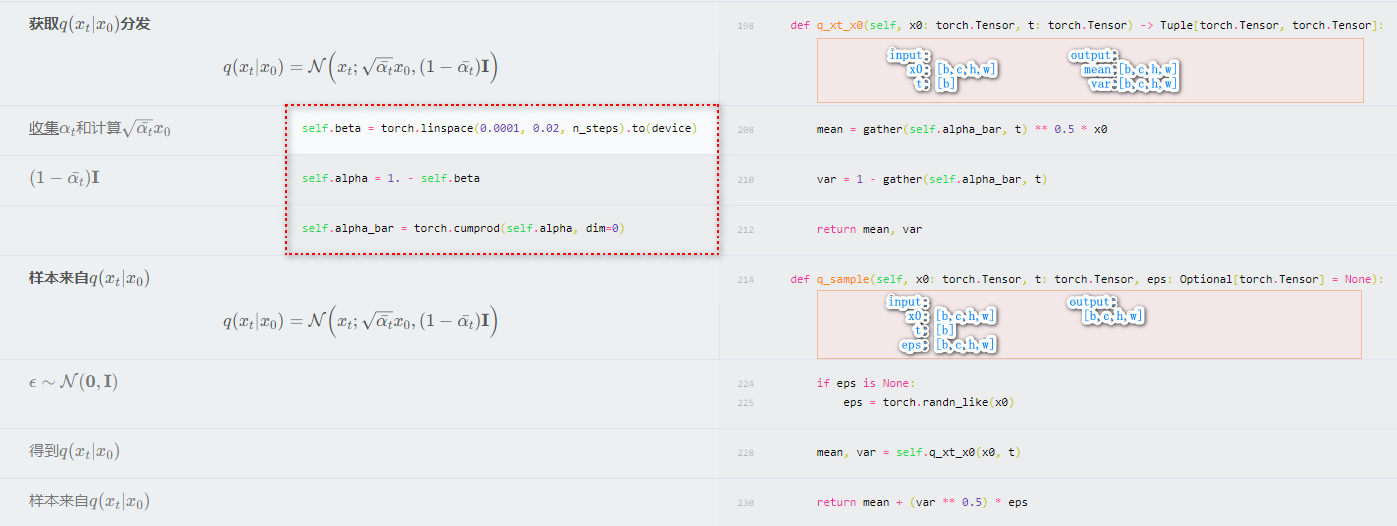
  • 3）任意 t 时刻的加躁结果：在逐步加噪的过程中，我们其实并不需要一步一步地从 x0,x1,...x_0,x_1,... 去迭代到 xtx_t。事实上，我们可以直接从 x0x_0 和固定序列 {βT∈(0,1)}t=1T\{\beta_T\in (0,1)\}_{t=1}^T 直接计算得到。定义 αt=1−βt,α‾t=∏i=1Tαi\alpha_{t}=1-\beta_{t},\overline{\alpha}_{t}=\prod_{i=1}^{T}\alpha_{i}，那么得到以下公式，其中 zt−1,zt−2,⋯∼N(0,I)\mathbf{z}_{t-1},\mathbf{z}_{t-2},\cdots\sim\mathcal{N}(\mathbf{0},\mathbf{I})，z‾t−2\overline{z}_{t-2} 是合并两个高斯分布。

xt=αtxt−1+1−αtzt−1=αtαt−1xt−2+1−αtαt−1z‾t−2=⋯=αˉtx0+1−αˉtzq(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)\begin{aligned}\mathbf{x}_{t}& =\sqrt{\alpha_{t}}\mathbf{x}_{t-1}+\sqrt{1-\alpha_{t}}\mathbf{z}_{t-1} \\&=\sqrt{\alpha_{t}\alpha_{t-1}}\mathbf{x}_{t-2}+\sqrt{1-\alpha_{t}\alpha_{t-1}}\overline{\mathbf{z}}_{t-2} \\&=\cdots \\&=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\mathbf{z} \\q\left(\mathbf{x}_{t}\mid\mathbf{x}_{0}\right)& =\mathcal{N}\left(\mathbf{x}_{t};\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0},\left(1-\bar{\alpha}_{t}\right)\mathbf{I}\right) \end{aligned}

  • 4） βt\beta_t 的设置：一般地，我们随着​ tt 的增大，数据越接近随机的高斯分布，βt\beta_t 的取值越来越大，所以 β1<β2<…<βT\beta_1<\beta_2<\ldots<\beta_T，所以 α‾1>α‾2>…>α‾T\overline{\alpha}_{1}>\overline{\alpha}_{2}>\ldots>\overline{\alpha}_{T}

DDPM 加躁时，如何推出 P(xt∣xt−1)P(x_t|x_{t-1}) 的分布？

  • q(xt∣xt−1)q(x_t|x_{t-1}) 是 xtx_t 在 x=xt−1x=x_{t-1} 下的条件概率分布，已知 x∼q(x)x\sim q(x)，I∼N(0,1)I\sim N(0,1)，βT\beta_T 是一个常数，如何推出 P(xt∣xt−1)∼N(xt;1−βtxt−1,βtI)P (x_t|x_{t-1})\sim N(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_tI)?
  • 1）在 DDPM（Denoising Diffusion Probabilistic Models）中，我们有一个马尔科夫链，其中每个状态 xt 都是前一个状态 xt-1 和高斯噪声的结果。这个过程可以写成以下公式，其中 εt 是从标准正态分布 N (0, 1) 采样的噪声，βt\beta_t 是一个小的时间步

xt=1−βtxt−1+βtεtx_t = \sqrt{1 - \beta_t} x_{t-1} + \sqrt{\beta_t} ε_t

  • 2）想要找到条件概率 p(xt∣xt−1)p(x_t|x_{t-1})，这是 xtx_t 给定 xt−1x_{t-1} 的概率。由于 xtx_t 是 xt−1x_{t-1} 和高斯噪声的线性组合，我们可以直接计算这个条件概率。首先，注意到 xt−1−βtxt−1x_t - \sqrt{1 - \beta_t} x_{t-1} 是高斯噪声 βtεt\sqrt{\beta_t} ε_t，所以它服从 N(0,βt)N(0, \beta_t)。因此，我们有，对于第二行公式来说，因为 xt−1x_{t-1} 是已知，可以认定是一个常量：

xt−1−βtxt−1=N(xt;0,βt)xt=N(xt;0,βt)+1−βtxt−1p(xt∣xt−1)=N(xt;1−βtxt−1,βt)\begin{array}{ll}x_t - \sqrt{1 - \beta_t} x_{t-1}= N(x_t; 0, \beta_t)\\x_t = N(x_t; 0, \beta_t)+\sqrt{1 - \beta_t} x_{t-1}\\p(x_t|x_{t-1}) = N(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t)\end{array}

  • 因为任何正态分布的线性变换仍然是正态分布。在这个例子中，线性变换是由 xt−1x_{t-1} 和高斯噪声的线性组合形成的

DDPM 加躁过程如何合并不同时刻的噪声？

  • 在求解从 x0x_0 推导 xnx_n 的过程中，涉及以下递归公式，不同时刻的噪声 ztz_t 如何合并为最终的噪声 zz

xt=αtxt−1+1−αtzt=αt(αt−1xt−2+1−αt−1zt−1)+1−αtzt=αtαt−1xt−2+(αt(1−αt−1)zt−1+1−αtzt)=αtαt−1xt−2+αt(1−αt−1)+(1−αt)zˉt=αtαt−1xt−2+1−αtαt−1zˉt=αtαt−1⋯α2α1x0+1−αtαt−1⋯α2α1z=αˉtx0+1−αˉtz\begin{aligned}\mathbf{x}_{t}& =\sqrt{\alpha_{t}}\mathbf{x}_{t-1}+\sqrt{1-\alpha_{t}}\boldsymbol{z}_{t} \\&=\sqrt{\alpha_t}\left(\sqrt{\alpha_{t-1}}\mathbf{x}_{t-2}+\sqrt{1-\alpha_{t-1}}\boldsymbol{z}_{t-1}\right)+\sqrt{1-\alpha_t}\boldsymbol{z}_t \\&=\sqrt{\alpha_{t}\alpha_{t-1}}\mathbf{x}_{t-2}+\left(\sqrt{\alpha_{t}(1-\alpha_{t-1})}\boldsymbol{z}_{t-1}+\sqrt{1-\alpha_{t}}\boldsymbol{z}_{t}\right) \\&=\sqrt{\alpha_{t}\alpha_{t-1}}\mathbf{x}_{t-2}+\sqrt{\alpha_{t}(1-\alpha_{t-1})+(1-\alpha_{t})}\bar{\boldsymbol{z}}_{t} \\&=\sqrt{\alpha_{t}\alpha_{t-1}}\mathbf{x}_{t-2}+\sqrt{1-\alpha_{t}\alpha_{t-1}}\bar{\boldsymbol{z}}_{t} \\&=\sqrt{\alpha_{t}\alpha_{t-1}\cdots\alpha_{2}\alpha_{1}}\mathbf{x}_{0}+\sqrt{1-\alpha_{t}\alpha_{t-1}\cdots\alpha_{2}\alpha_{1}}\boldsymbol{z} \\&=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\boldsymbol{z}\end{aligned}

  • 在由 xt−2x_{t-2} 计算 xtx_t 时，其分解公式

xt=αtαt−1xt−2+αt−αtαt−1zt−2+1−αtzt−1x_t=\sqrt{\alpha_{t}\alpha_{t-1}}\mathbf{x}_{t-2}+\sqrt{\alpha_{t}-\alpha_{t}\alpha_{t-1}}\mathbf{z}_{t-2}+\sqrt{1-\alpha_{t}}\mathbf{z}_{t-1}

，其中 zt−2,zt−1∼N(0,1)z_{t-2}, z_{t-1}\sim N(0,1)，所以 αt−αtαt−1zt−2+1−αtzt−1\sqrt{\alpha_{t}-\alpha_{t}\alpha_{t-1}}\mathbf{z}_{t-2}+\sqrt{1-\alpha_{t}}\mathbf{z}_{t-1} 分别服从 N(0,αt−αtαt−1),N(0,1−αt)N (0,\alpha_{t}-\alpha_{t}\alpha_{t-1}),N(0,1-\alpha_{t})，根据两个正态分布相加、相减、相乘后的分布情况，αt−αtαt−1zt−2+1−αtzt−1\sqrt{\alpha_{t}-\alpha_{t}\alpha_{t-1}}\mathbf{z}_{t-2}+\sqrt{1-\alpha_{t}}\mathbf{z}_{t-1} 还是服从高斯分布，并且服从 N(0,1−αtαt−1)N(0,1-\alpha_t\alpha_{t-1})

  • 递归下去，所有时刻的 z 相加，服从 N(0,1−α‾)N(0,1-\overline{\alpha})

DDPM 的去躁过程（Denoise Process）？

  • 1）逆扩散过程近似 pθp_\theta：从一个随机的高斯分布 N(0,1)N(0,1) 中重建出一个真实的原始样本，也就是从一个完全杂乱无章的噪声图片中得到一张真实图片。但是，由于需要从完整数据集中找到数据分布，我们没办法很简单地预测 q(xt−1∣xt)q (x_{t-1}|x_t)，因此我们需要学习一个模型 pθp_\theta ​来近似模拟这个条件概率，从而运行逆扩散过

pθ(x0:T)=p(xT)∏t=1Tpθ(xt−1∣xt)pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),∑θ(xt,t))\begin{aligned}p_\theta\left(\mathbf{x}_{0:T}\right)&=p(\mathbf{x}_T)\prod_{t=1}^Tp_\theta\left(\mathbf{x}_{t-1}\mid\mathbf{x}_t\right)\\p_\theta\left(\mathbf{x}_{t-1}\mid\mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1};\mu_\theta(\mathbf{x}_t,t),\sum_\theta(\mathbf{x}_t,t)\right)\end{aligned}

  • 2）后验扩散条件概率 q(xt−1∣xt,x0)q(x_{t-1}|x_t,x_0)：在逆扩散过程中，如果我们给定了 xtx_t 和 x0x_0 ​, 那我们是可以计算出​ xt−1x_{t-1} 的，即后验扩散条件概率​ q(xt−1∣xt,x0)q (x_{t-1}|x_t,x_0) 是可以计算的，计算得 q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_{t-1};\tilde{\boldsymbol{\mu}}(\mathbf{x}_t,\mathbf{x}_0),\tilde{\boldsymbol{\beta}}_t\mathbf{I})，根据贝叶斯公式得最终解

q(xt−1∣xt)∼N(xt−1;μt(xt),σt2)=N(xt−1;1αt(xt−1−αt1−αˉtϵ),(1−αˉt−1)(1−αt)1−αˉtz)\begin{aligned}q(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})& \sim\mathcal{N}\left(\mathbf{x}_{t-1};\boldsymbol{\mu}_{t}(\mathbf{x}_{t}),\boldsymbol{\sigma}_{t}^{2}\right) \\&=\mathcal{N}\left(\mathbf{x}_{t-1};\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon\right),\frac{(1-\bar{\alpha}_{t-1})(1-\alpha_{t})}{1-\bar{\alpha}_{t}}z\right)\end{aligned}

  • 后向去躁可以看成是一个 MCMC 采样过程，而其中实际每一步的转移方程都是沿着往数据分布的梯度方向迈进，且该方向由我们神经网络的输出来拟合

DDPM 去躁时为什么要向 Unet 输入 t？

  • 在 Denoise Process 当中，用 XtX_t 去预测 Xt−1X_{t-1} 的图片，直接预测 Xt−1X_{t-1} 比较麻烦，因为 Xt−1X_{t-1} 的分布未知，但是加躁是从标准高斯分布采样的，这是明确的，所以最终使用 Unet 预测噪声即可
  • 在预测噪声时，向 Unet 输入的是 Xt,tX_t,t 共 2 个值，其中 t 表示 Denoise Process 到第几步，这和 transformer 中的位置编码一样，这正余弦编码或者是一个傅里叶特征
  • 另外，在逐步恢复 Xt−1X_{t-1} 的过程中，U-net 是参数共享的，加入 time embedding 能够根据不同的输入而生成不同的输出

DDPM 的训练？

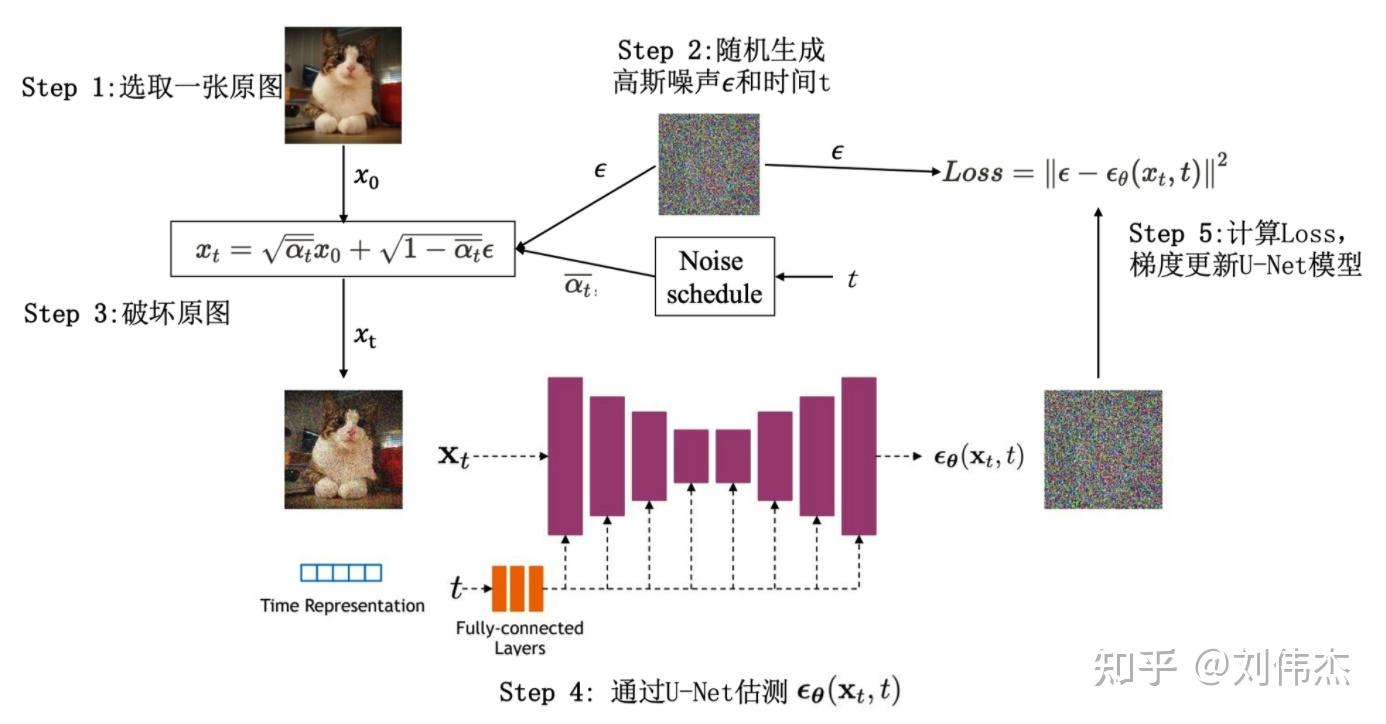
  • 1）从训练数据中，抽样出一张图片 x0∼q(x)x_0\sim q(x)
  • 2）随机抽样出一个 timestep，即 t∼Uniform(1,...,T)t\sim Uniform(1,...,T)
  • 3）随机抽样出一个噪声，即 ϵ∼N(0,I)\epsilon\sim\mathcal{N}(0,I)
  • 4）计算 loss：ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)\epsilon-\epsilon_{\theta}\big(\sqrt{\bar{\alpha}_{t}}x_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon,t\big)，其中 ϵθ\epsilon_{\theta} 表示 UNet 架构的去噪模型
  • 5）计算梯度，更新模型
  • 6）重复上面过程，直至收敛

DDPM 的推理？

  • 1）从标准高斯分布采样数据 xT∼N(0,1)x_T\sim N(0,1)
    1. 从 T 遍历到到 1，共遍历 T 次以下操作
  • 3）从标准高斯分布采样数据 z∼N(0,1)z \sim N(0,1)
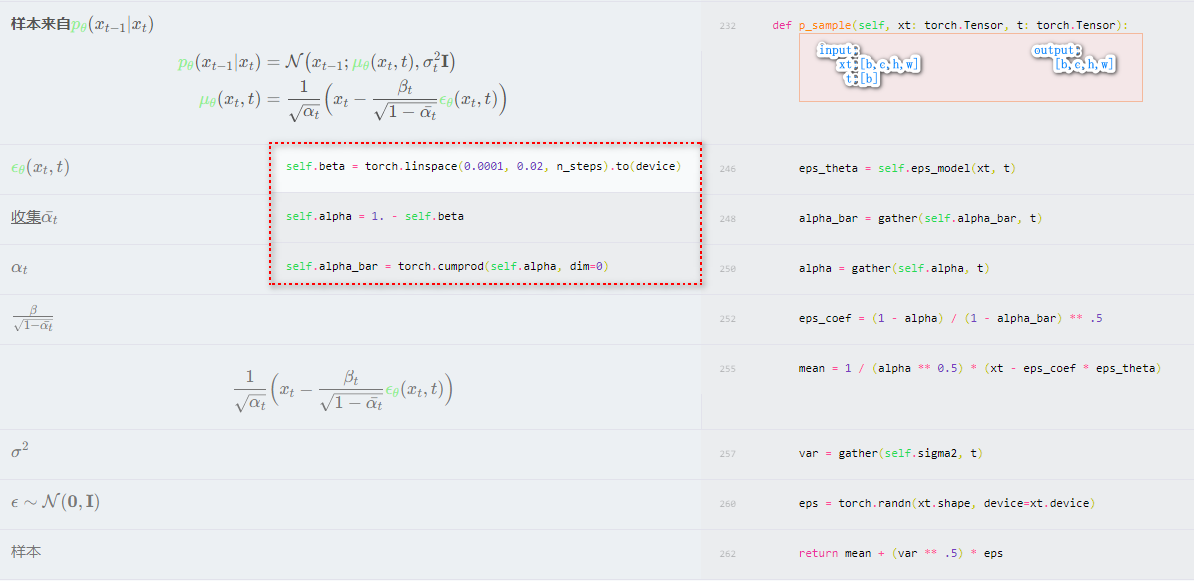
  • 4）按照公式还原 xT−1x_{T-1}，这个公式是根据严谨的数学流程推导出来的，其中 σt2=(1−αt)(1−αˉt−1)1−αˉt\sigma_t^2=\frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}，在 DDPM 论文中，已通过实验证明可用 σt2=βt\sigma_{t}^{2}=\beta_{t} 替

xt−1=1αt(xt−1−αt1−αˉtϵθ(xt,t))+σtz\mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\boldsymbol{\epsilon}_{\theta}(\mathbf{x}_{t},t)\right)+\sigma_{t}\mathbf{z}

  • 5）遍历 T 次后，输出 x0x_0，完成图片还原

DDPM 的损失函数？

  • 和 VAE 相似，DDPM 也是最小化负对数似然函数的下确界

log⁡pθ(x0)=log⁡∫pθ(x0:T)dx1:T=log⁡∫pθ(x0:T)q(x1:T∣x0)q(x1:T∣x0)dx1:T≥Eq(x1:T∣x0)[log⁡pθ(x0:T)q(x1:T∣x0)]\begin{aligned}\log p_{\theta}\left(\mathbf{x}_{0}\right)& =\log\int p_{\theta}\left(\mathbf{x}_{0:T}\right)d\mathbf{x}_{1:T} \\&=\log\int\frac{p_{\theta}\left(\mathbf{x}_{0:T}\right)q\left(\mathbf{x}_{1:T}\mid\mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{1:T}\mid\mathbf{x}_{0}\right)}d\mathbf{x}_{1:T} \\&\geq\mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}\left[\log{\frac{p_{\theta}\left(\mathbf{x}_{0:T}\right)}{q\left(\mathbf{x}_{1:T}\mid\mathbf{x}_{0}\right)}}\right]\end{aligned}

进一步得

L=−VLB=Eq(x1:T∣x0)[log⁡q(x1:T∣x0)pθ(x0:T)]=DKL(q(xT∣x0)∥pθ(xT))⏟LT+∑t=2TDKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))⏟Lt−Eq(x1∣x0)[log⁡pθ(x0∣x1)]⏟L0\begin{array}{ll}\mathcal{L}=-\mathrm{VLB}=\mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}\left[\log\frac{q\left(\mathbf{x}_{1:T}\mid\mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0:T}\right)}\right]\\=\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{T}\mid\mathbf{x}_{0}\right)\|p_{\theta}\left(\mathbf{x}_{T}\right)\right)}_{\mathcal{L}_{T}}+\sum_{t=2}^{T}\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1}\mid\mathbf{x}_{t},\mathbf{x}_{0}\right)\|p_{\theta}\left(\mathbf{x}_{t-1}\mid\mathbf{x}_{t}\right)\right)}_{\mathcal{L}_{t}}\underbrace{-\mathbb{E}_{q(\mathbf{x}_{1}\mid\mathbf{x}_{0})}[\log p_{\theta}(\mathbf{x}_{0}\mid\mathbf{x}_{1})]}_{\mathcal{L}_{0}}\end{array}

第一项约束最终第 T 步得到的加噪结果 xTx_T 接近完成高斯噪声，最后一项约束模型生成的结果与真值接近，而中间的 t-1 项约束逆向过程的马尔科夫链中，神经网络估计出的每一个条件分布接近于对应的真实的数据分布，中间项计算

DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))=DKL(N(xt−1;μt(xt,x0),σt2)∥N(xt−1;μθ(xt,t),σt2))=12(n+1σt2∥μt(xt,x0)−μθ(xt,t)∥2−n+log⁡1)=12σt2∥μt(xt,x0)−μθ(xt,t)∥2\begin{aligned}&D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1}\mid\mathbf{x}_{t},\mathbf{x}_{0}\right)\|p_{\theta}\left(\mathbf{x}_{t-1}\mid\mathbf{x}_{t}\right)\right) \\&= D_{\mathrm{KL}}\left(\mathcal{N}\left(\mathbf{x}_{t-1};\boldsymbol{\mu}_{t}\left(\mathbf{x}_{t},\mathbf{x}_{0}\right),\boldsymbol{\sigma}_{t}^{2}\right)\|\mathcal{N}\left(\mathbf{x}_{t-1};\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t},t\right),\boldsymbol{\sigma}_{t}^{2}\right)\right) \\&= \frac{1}{2}\left(n+\frac{1}{\sigma_{t}^{2}}\|\boldsymbol{\mu}_{t}\left(\mathbf{x}_{t},\mathbf{x}_{0}\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t},t\right)\|^{2}-n+\log1\right) \\&= {\frac{1}{2\sigma_{t}^{2}}}\|\boldsymbol{\mu}_{t}\left(\mathbf{x}_{t},\mathbf{x}_{0}\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t},t\right)\|^{2} \end{aligned}

  • 其实就是使用网络预测随机噪声，然后和真实添加的噪声计算 MSE 损失，并更新网络
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"):
    	# 先采样噪声
    	if noise is None:
    		noise = torch.randn_like(x_start)
    	# 用采样得到的噪声去加噪图片
    	x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
    	predicted_noise = unet_model(x_noisy, t)
    	# 根据加噪了的图片去预测采样的噪声
    	if loss_type == 'l1':
    		loss = F.l1_loss(noise, predicted_noise)
    	elif loss_type == 'l2':
    		loss = F.mse_loss(noise, predicted_noise)
    	elif loss_type == "huber":
    		loss = F.smooth_l1_loss(noise, predicted_noise)
    	else:
    		raise NotImplementedError()
    	return loss

GAN、VAE、DDPM 的区别？

  • 就学习原始数据分布来说，GAN 通过神经网络直接拟合数据分布；VAE 不直接学习数据分布，而是学习数据的确定性的潜在分布，通过对确定性的潜在分布去接近数据分布；DDPM 则将通过不断将确定性分布和数据分布采样相加，直到达到一个已知的简单分布（如高斯分布），然后反向从已知分布逐步采样去掉确定性分布，最终得到接近原始数据分布
  • 就网络学习方式而言：GAN 由生成器和判别器对抗训练得到；VAE 将学习过程分为编码和解码阶段，在编码阶段学习确定性潜在分布，解码阶段从潜在分布重构样本，这个网络需要监督潜在分布和重构质量；DDPM 由确定性的加躁过程和神经网络参与的去躁过程组成，网络用于估计每一次加躁的噪声
  • 就生成样本的方式而言：不考虑条件因素，GAN 直接基于随机变量生成样本；VAE 利用解码器从潜在分布生成样本；DDPM 基于随机变量，然后使用神经网络去噪 t 次生成样本
  • 这 3 种模型都是无监督学习模型，用于样本生成，通常 GAN 生成的效果更好，但是不好训练，也不好控制；VAE 生成图像比较模糊，但是可以通过控制潜在分布进而控制生成效果；DDPM 需要去躁 t 次，生成速度较慢，但是生成效果很好

参考：

  1. DDPM 解读（一）| 数学基础，扩散与逆扩散过程和训练推理方法 - 知乎
  2. 全网最简单的扩散模型 DDPM 教程 - 知乎
  3. DDPM (Denoise Diffusion Probabilistic Model) 理论梳理 (含公式推导，小白) - 知乎
  4. 深入浅出扩散模型 (Diffusion Model) 系列：基石 DDPM（源码解读篇） - 知乎
  5. 扩散模型 Diffusion Model 与 DDPM_time embedding-CSDN 博客
  6. 如何通俗理解扩散模型？ - 知乎
  7. 去噪扩散概率模型 (DDPM)
  8. A friendly Introduction to Denoising Diffusion Probabilistic Models | by Antony M. Gitau | Medium