图论---问题篇

发表于 2018-06-28 更新于 2023-10-24 分类于 0-数据基础， F-图论阅读次数：本文字数： 2.4k 阅读时长 ≈ 2 分钟

图论中的算法基本都是提出后,经过检验的.我就不讨论算法很基础的原理,只是从看懂一个算法的角度去学习.本着不花时间去重复别人优秀工作的原则,本文中很多部分引用了别人的工作,甚至是照搬过来,因为我觉得算法这东西已经类似真理,证明不需要你,你可以看得懂,别人也可以,只是表达方式不同,别人有优秀的表达方式,我为什么不用呢!

问题类

路径问题

柯尼斯堡七桥问题

这个问题是基于一个现实生活中的事例：当时东普鲁士柯尼斯堡（今日俄罗斯加里宁格勒）市区跨普列戈利亚河两岸，河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？

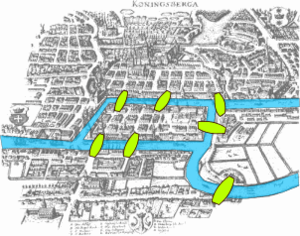
摘自:

维基百科-柯尼斯堡七桥问题

哈密顿回路问题

哈密顿图是一个无向图,由指定的起点前往指定的终点，途中经过所有其他节点且只经过一次

哈密顿回路: 闭合的哈密顿路径称作哈密顿回路
哈密顿路径: 含有图中所有顶点的路径称作哈密顿路径。

摘自:

百度百科-哈密顿回路

最小生成树问题

最小生成树是一副连通加权无向图中一棵权值最小的生成树。具体定义为: 在一给定的无向图 G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即 ( u , v ) ∈ E ，而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即 T ⊆ E 且 (V, T) 为树，使得下面的值最小.

1
2
3

$$
w(T)=\sum_{(u,v)\subseteq E}{w(u,v)}
$$

可以描述为以下问题,有一个有权无向图,找到路径把所有顶点连起来,并保证边上权重和最小. 所以最小生成树也称为:最小权重生成树

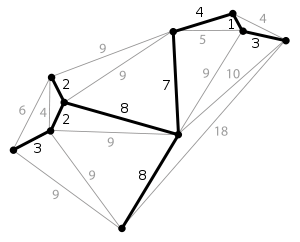
一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和。广义上而言，对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。

以有线电视电缆的架设为例，若只能沿着街道布线，则以街道为边，而路口为顶点，其中必然有一最小生成树能使布线成本最低。

摘自:

维基百科-最小生成树

中国邮路问题

也称中国邮递员问题,此问题为在一个连通的无向图中找到一最短的封闭路径，且此路径需通过所有边至少一次。

注意:下面有一个旅行商问题是经过所有点一次,和这个边不同.

简单来说，邮递员问题就是在一个已知的地区，邮差要设法找到一条最短路径，可以走过此地区所有的街道，且最后要回到出发点.

摘自:

维基百科-邮递员问题

最短路问题

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。算法具体的形式包括：

确定起点的最短路径问题 - 即已知起始结点，求最短路径的问题。适合使用Dijkstra算法。
确定终点的最短路径问题 - 与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径。
全局最短路径问题 - 求图中所有的最短路径。适合使用Floyd-Warshall算法。

用于解决最短路径问题的算法被称做“最短路径算法”，有时被简称作“路径算法”。最常用的路径算法有：

Dijkstra算法
A*算法
Bellman-Ford算法
SPFA算法（Bellman-Ford算法的改进版本）
Floyd-Warshall算法
Johnson算法
Bi-Direction BFS算法

摘自:

维基百科-最短路问题

斯坦纳树

斯坦纳树问题是组合优化问题，与最小生成树相似，是最短网络的一种。最小生成树是在给定的点集和边中寻求最短网络使所有点连通。而最小斯坦纳树允许在给定点外增加额外的点，使生成的最短网络开销最小。

展示问题,以供理解:

1.平原上的三个城镇间要兴建一个公用的煤气供应站，在选址问题上，要考虑的主要问题是使由供应站到三个城镇的输送管道的总长最短。如何去寻找合适地点？
2.假若要建的是一个垃圾处理站，要修建三条公路将垃圾站与三个城镇连起来。这时，因为三个城镇的居民的数目或工业性质等的不同，每天运送垃圾使用的车辆数目各不相同，运输的费用也就各异。因此，选取地点时，如果仍考虑使三条公路的总长最小，就不合理了。这时应该考虑：先计算出三个城镇单位时间内生产的垃圾数量的百分比（或每日运输费用的百分比），如何选取地点，使得每个城镇垃圾运输数量与公路里程的乘积之和为最小。

摘自:

百度百科-斯坦纳树

旅行商问题（NP困难）

假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

注意：上面有一个中国邮路问题是经过所有边一次,和这个点不同.

摘自:

百度百科-TSP问题

网络流与匹配

最大流问题

在优化理论中,最大流问题涉及到在一个单源点、单汇点的网络流中找到一条最大的流。
最大流问题可以被看作是一个更复杂的网络流问题的特殊情况,。s-t流（从源点s到汇点t）的最大值等于s-t割的最小容量，这被称为最大流最小割定理。

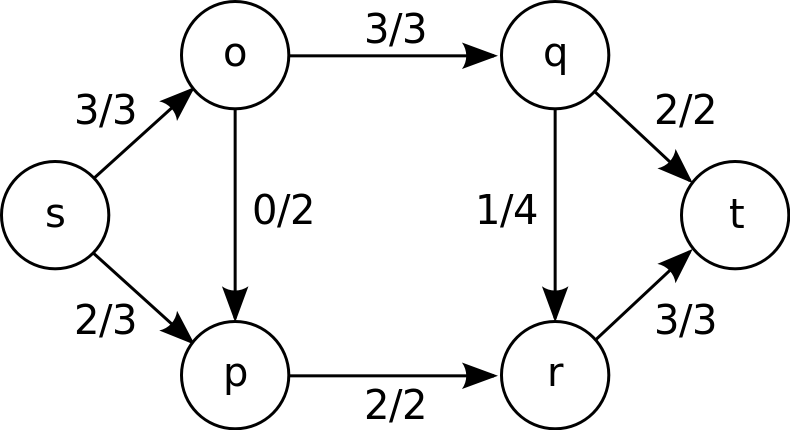
最小费用最大流问题: 在一个网络中每段路径都有“容量”和“费用”两个限制的条件下，此类问题的研究试图寻找出：流量从A到B，如何选择路径、分配经过路径的流量，可以达到所用的费用最小的要求。
在实际中：n辆卡车要运送物品，从A地到B地。由于每条路段都有不同的路费要缴纳，每条路能容纳的车的数量有限制，如何分配卡车的出发路径可以达到费用最低，物品又能全部送到。

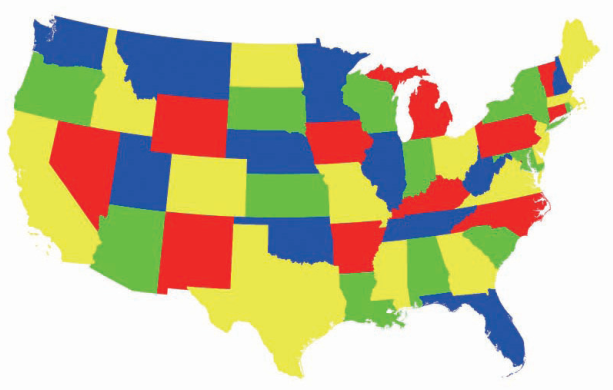
摘自: