STN

发表于 2022-12-06 更新于 2025-01-18 分类于 2-深度学习， B-视觉模型， 1-基础视觉任务CNN ，人体姿势估计阅读次数：本文字数： 1.1k 阅读时长 ≈ 1 分钟

STN 通过网络学习变换参数，并使用双线性插值使得网络可训练，以达到可以动态学习图片变换参数的可能，实现对不同图片的变换。可用于需要姿态校正的任务上，如 OCR 文字摆正，生成高质量的单人人体区域，3 D 数据变换

在进行计算机视觉任务时，常常希望模型对物体姿势或位置的变化具有一定的不变性，传统方法是使用仿射变换处理图片，但是每张图片的仿射变换参数不一样；深度学习的卷积和池化有一定程度上实现平移不变性，但是比较难实现旋转不变性、缩放不变性
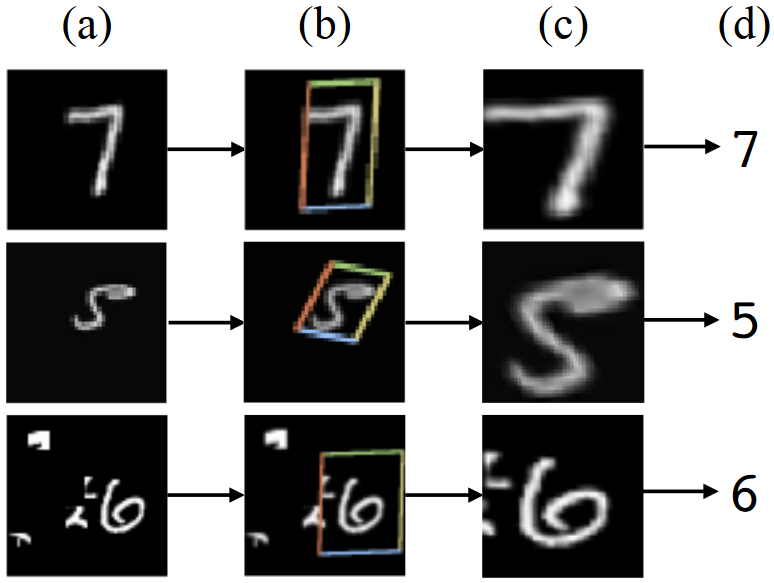
能不能通过模型去学习这种 “变换过程” 呢？STN 给出答案，上图 abc 分别是原图、变换矩阵处理区域、处理后的图片。所谓的变换过程，就是学习仿射变换矩阵的 6 或 9 个参数，为了使得这 9 个参数可微，使用双线性插值对变换后的矩阵采样。

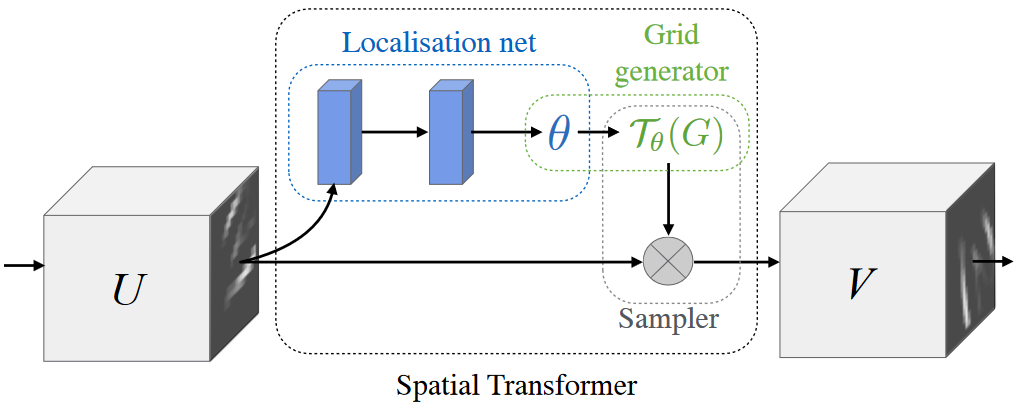
STN 的网络结构包含以下 3 个部分，其中 U 是图片或特征，V 是经过变换后的输出
Localisation net：这是一个回归子网络，输出的维度取决于变换规则，如果进行的是仿射变换，则输出 $R^{2\times3}$ 的 6 个实数，如果是投影变换，输出 $R^{3\times3}$ 的 9 个实数。这些实数表示仿射矩阵的值，假设 U=(N, C, H, W)，则 Localisation net 输出是矩阵 L (N, 2,3)
Grid generator：一个根据输出大小设计的一个 grid 生成器，如网络输出分辨率是 (H’, W’)，那么 Grid generator 首先生成 (N, 3, H’, W’) 的矩阵 G，其中 3 表示 grid 的位置，如矩阵 G 第 2 位置是 G [N, 3,0,1]=Nx (0,1,0), 矩阵 G 第 5 位置是 G [N, 3,0,4]=Nx (0,4, 0)。得到矩阵 G 的目的是与仿射矩阵 L 相乘，计算 (H’, W’) 的输出对应原始输入 U 的什么位置，即矩阵 GG= $L\cdot G$ =(N, 2, H’, W’)
Sampler：根据输入 U=(N, C, H, W) 和输出每个 grid 对应原图位置 GG= $L\cdot G$ =(N, 2, H’, W’) 去生成最后的输出。理论上既然 GG 的第二维度表示 U 位置，那么直接取值即可，但是此时的 GG 矩阵第二维度包含小数，不是整数，不能直接取值。借鉴 Mask RCNN 的 ROI Algin 方法，可以由第二维度的取值可以由四周的四个整数求得，最后输出是 V=(N, C, H’, W’)

参考：