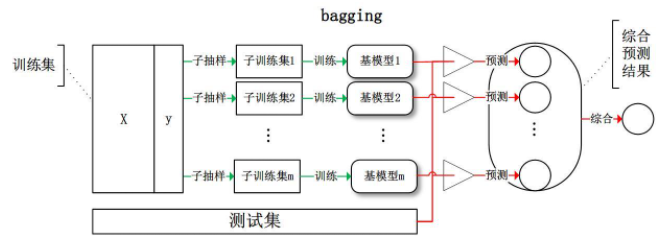
装袋算法 - Bagging
Bagging 通过将数据集划分为多分,对每一份建模,只要各个分类器准确率在 50% 以上,那么 N 个分类器的准确率就有可能大于 N-1 个分类器
什么是装袋算法 (Bagging)?
![]()
- Bagging 是并行模式,意味着三个臭皮匠各搞各的然后将最后结果进行融合以期带来提升,这里 bagging 是一个合成词汇,本意为 booststrap aggregating
- bagging 算法要求集成学习各弱学习器之间要求算法尽可能是随机的,同时也有准确率的最低要求,即不能低于 50%,否则会对集成效果带来负作用
- bagging 算法会降低方差 (Bias),但不会降低偏差 (Variabce)
- 常见三种装袋模型:装袋决策树(BaggedDecisionTrees)、随机森林 (Random Forest)、极端随机树
什么是 Bagging (袋装方法)?
- 在集合算法中,Bagging 形成了一类算法,它在原始训练集的随机子集上建立了几个黑箱估计器的实例,然后将它们各自的预测结果汇总,形成最终的预测结果。
- 这些方法被用作减少基础估计器(如决策树)的方差的一种方法,通过在其构建过程中引入随机化,然后将其集合起来。在许多情况下,Bagging 构成了一种非常简单的改进单一模型的方法,而不需要调整基本的基础算法。由于它们提供了一种减少过拟合 (overfitting) 的方法,袋化方法对强大而复杂的模型(如完全发展的决策树)效果最好
1
2
3
4
5>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
... max_samples=0.5,
max_features=0.5)
装袋算法 (Bagging) 的分类?
- 根据弱分类器的采样方式,将 Bagging 算法分为 4 类
- 1. 仅对样本维度采样(行采样),且采样是有放回的: 意味着每个弱学习器的 K 个采样样本中可能存在重复的样本,此时对应 bagging 算法,这里 bagging=bootstrap aggregating
- 2. 仅对样本维度采样(行采样),但采样是无放回的: 意味着对于每个弱学习器的 K 个采样样本是完全不同的,由于相当于是每执行一次采样,则该样本就被舍弃掉 (pass),所以此时算法叫做 pasting
- 3. 对于特征维度进行随机采样(列采样) : 比如说每个弱学习器都选用所有的样本参与训练,但各学习器选取参与训练的特征是不一致的,训练出的算法自然也是具有随机性的,可以满足集成的要求。此时,对应算法叫做 subspaces,中文译作子空间,具体说是特征维度的子空间
- 4. 既有样本维度的随机(行采样),也有特征维度的随机(列采样) : 每个弱学习器既执行行采样、也有列采样,得到的弱学习器其算法随机性应该更强。当然,这种算法被称作是 patches,比如随机森林就属于这种。实际上,随机森林才是最为广泛使用的 bagging 流派集成学习算法
装袋算法 (Bagging) 对列随机采样训练分类器时,是否可以像行采样一样执行有放回操作?
- 又放回的行采样会导致分类器可能使用重复的样本,对结果有影响
- 假设列采样是有放回的,会导致重复特征或复制特征,不能带来学习效果的改变
装袋算法 (Bagging) 的有放回行采样有什么特点?
- 有放回采样中,预计有 **36.8%** 的样本不会被用于训练,也就意味着这些样本可以天然的作为测试集用于评估集成学习模型效果
- 对于一个样本,它在某一次含 m 个样本的训练集的随机采样中,每次被采集到的概率是 1/m。不被采集到的概率为 1−1/m,若 m 次采样都没有被采集中的概率是 (1−1/m)^m, 当 m⇒∞时,(1−1/m)^m⇒1/e≃0.368,即每轮随机采样中,训练集中大约有 36.8% 的数据没有被采样集采集中
装袋算法 (Bagging) 如何进程综合决策的?
- hard voting: 以二分类问题为例,hard voting 综合决策是直接统计所有弱学习器的结果,然后取其中结果最多的那一类作为最终结果
- soft voting: 统计各弱学习器的分类概率,并分别计算所有弱学习器中两类的概率之和,以概率之和较大者作为最终结果
装袋算法 (Bagging) 有哪些优点?
- 训练方便: 训练一个 Bagging 集成与直接使用基分类器算法训练一个学习器的复杂度同阶,说明 Bagging 是一个高效的集成学习算法
- 适用多分类与回归: 与标准的 AdaBoost 算法只适用于二分类问题不同,Bagging 能不经过修改用于多分类、回归等任务
- 可进行包外估计(out-of-bag estimate) : 由于每个基学习器只使用 63.2% 的数据,所以剩下 36.8% 的数据可以用来做验证集来对泛化性能进行 “