C01 - 图像特征提取与检测

发表于 2022-06-02 更新于 2025-01-18 分类于 3-编程实践， E-OpenCV ， OpenCV使用指南阅读次数：本文字数： 45k 阅读时长 ≈ 41 分钟

介绍图像的目标特征及其计算方法

图像上的目标特征？

目标：通过图像分割获得多个区域，得到区域内的像素集合或区域边界像素集合。我们把感兴趣的人或物称为目标，目标所处的区域就是目标区域
目标特征：针对于图像中的某个目标而言的。图像分割之后，还要对目标区域进行适当的表示和描述，以便下一步处理。“表示” 是直接具体地表示目标，以节省存储空间、方便特征计算。目标的表示方法，有链码、多边形逼近、斜率标记图、边界分段、区域骨架；“描述” 是对目标的抽象表达，在区别不同目标的基础上，尽可能对目标的尺度、平移、旋转变化不敏感

图像上目标特征有哪些？

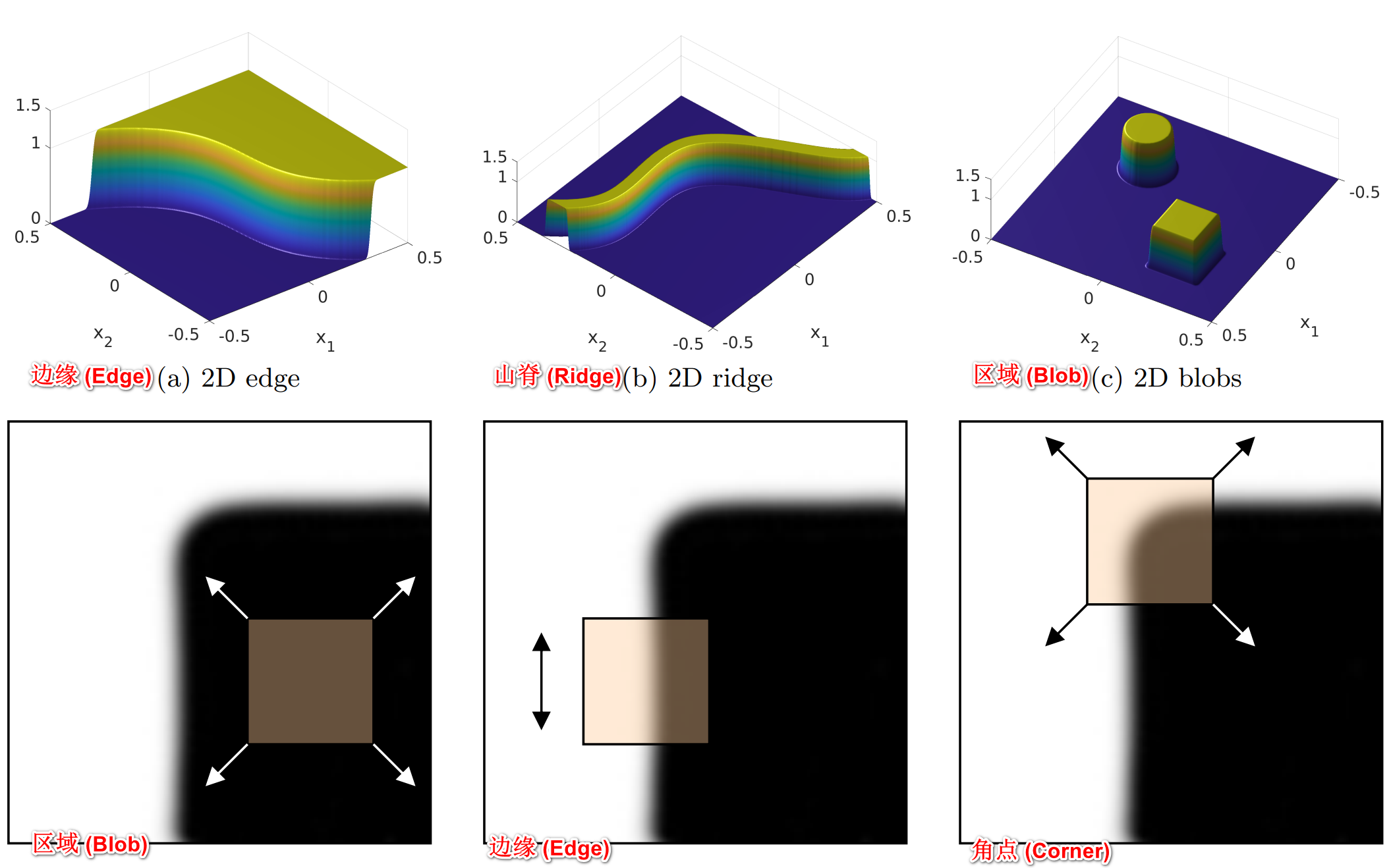
在图像处理和计算机视觉领域，图像特征可以用来解决目标识别、图像匹配、视觉跟踪、三维重建等一系列问题。图像特征主要包括三种类型：(1) 角点 (Corner)；(2) 边缘 (Edge)；(3) 区域 (Blob)；(4) 山脊 (Ridge)，其实就是点、线、面、曲线
角点：应用最为广泛，因为角点在任意方向的一个微小变动都会引起图像灰度的很大变化。“角点”(conrner) 也称之为 “兴趣点”(interest point) 或 “关键点”(key point) 或 “特征点”（feature）
孤立的点：与角点不同，孤立的点是一个被背景像素围绕的前景像素，或一个被前景像素围绕的背景像素
线与曲线：是一条细边缘线段，其两侧的背景灰度与线段的像素灰度存在显著差异
边缘：区别于线，一般指局部不连续的的图像特征，边缘点是灰度阶跃变化的像素点，即灰度值变化显著，导数较大或极大的地方
面：图片上的一个区域

图像的特征检测与匹配？

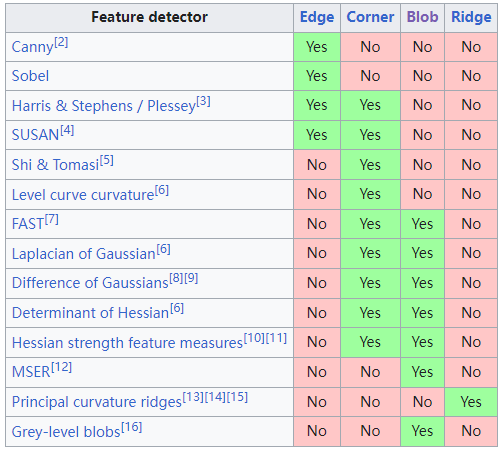
特征检测：特征检测的结果是把图像上的点分为不同的子集，这些子集往往属于孤立的点、连续的曲线或者连续的区域
特征点：由关键点（key point）和描述子（Descriptor）组成，其中，描述子通常是一个向量，描述了该关键点周围的像素信息。只要两个特征点的描述子在向量空间上的距离相近，就可以认为它们是相同的特征点

目标的 “边界特征” 描述子？

目标的边界描述符（Boundary descriptors），也称为边界描述子。轮廓就是对目标边界的描述，轮廓属性是基本的边界描述子，例如：
边界的长度：轮廓线的像素数量是边界周长的近似估计
边界的直径：边界长轴的长度，等于轮廓最小矩形边界框的长边长度
边界的偏心率：边界长轴与短轴之比，等于轮廓最小矩形边界框的长宽比
边界的曲率：相邻边界线段的斜率差
链码：通过规定长度和方向的直线段来表示边界
傅里叶描述符：对二维边界点进行离散傅里叶变换得到的傅里叶系数，对旋转、平移、缩放和起点不敏感
统计矩：把边界视为直方图函数，用图像矩对边界特征进行描述，具有平移、灰度、尺度、旋转不变性

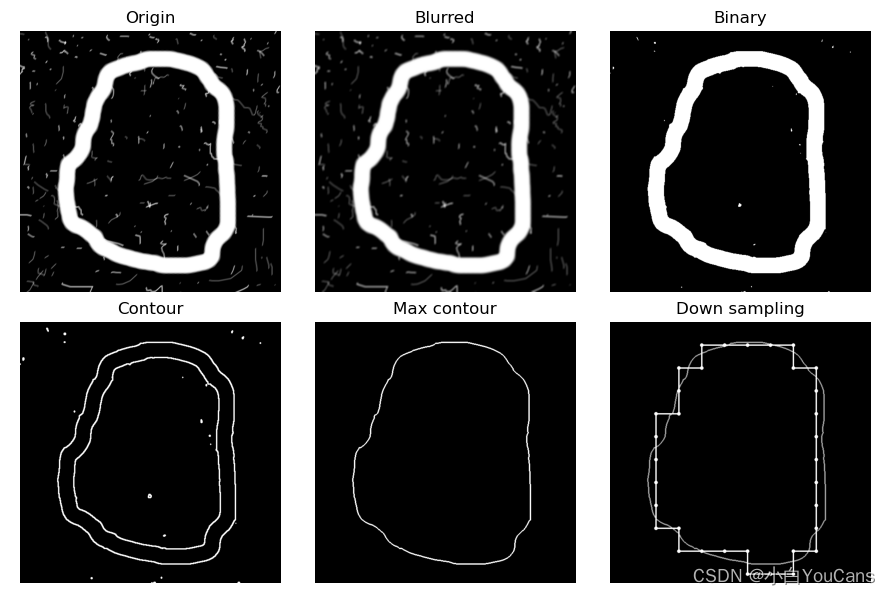
目标轮廓的闭合曲线弗里曼链码（Freeman chain code）？

链码表示基于线段的 4 连通或 8 连通（参考：如何认识 OpenCV 的线型 lineType）。弗里曼链码使用一种编号方案来对每个线段的方向进行编号

def FreemanChainCode(cLoop, gridsep=1):  # 由闭合边界点集生成弗里曼链码
	# Freeman 8 方向链码的方向数
	dictFreeman = {(1, 0): 0, (1, 1): 1, (0, 1): 2, (-1, 1): 3, (-1, 0): 4, (-1, -1): 5, (0, -1): 6, (1, -1): 7}
	diff_cLoop = np.diff(cLoop, axis=0) // gridsep  # cLoop 的一阶差分码
	direction = [tuple(x) for x in diff_cLoop.tolist()]
	codeList = list(map(dictFreeman.get, direction))  # 查字典获得链码
	code = np.array(codeList)  # 转回 Numpy 数组
	return code
# 计算目标轮廓曲线的弗里曼链码
img = cv2.imread("../images/Fig1105.tif", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 灰度图像
blur = cv2.boxFilter(gray, -1, (5, 5))  # 盒式滤波器，9*9 平滑核
_, binary = cv2.threshold(blur, 200, 255, cv2.THRESH_OTSU + cv2.THRESH_BINARY)
# 寻找二值化图中的轮廓，method=cv2.CHAIN_APPROX_NONE 输出轮廓的每个像素点
contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)  # OpenCV4~
# 绘制全部轮廓，contourIdx=-1 绘制全部轮廓
imgCnts = np.zeros(gray.shape[:2], np.uint8)  # 绘制轮廓函数会修改原始图像
imgCnts = cv2.drawContours(imgCnts, contours, -1, (255, 255, 255), thickness=2)  # 绘制全部轮廓
# 获取最大轮廓
cnts = sorted(contours, key=cv2.contourArea, reverse=True)  # 所有轮廓按面积排序
cnt = cnts[0]  # 第 0 个轮廓，面积最大的轮廓，(1361, 1, 2)
maxContour = np.zeros(gray.shape[:2], np.uint8)  # 初始化最大轮廓图像
cv2.drawContours(maxContour, cnt, -1, (255, 255, 255), thickness=2)  # 绘制轮廓 cnt
print("len(contours) =", len(contours))  # 所有轮廓的列表 24
print("area of max contour: ", cv2.contourArea(cnt))  # 轮廓面积 152294.5
print("perimeter of max contour: {:.1f}".format(cv2.arcLength(cnt, True)))  # 轮廓周长 1525.4
# 向下降采样，简化轮廓的边界
gridsep = 50  # 采样间隔
cntPoints = np.squeeze(cnt)  # 删除维度为1的数组维度，(1361,1,2)->(1361,2)
subPoints = boundarySubsample(cntPoints, gridsep)  # 自定义函数，通过向下采样简化轮廓
print("points of contour:", cntPoints.shape[0])  # 原始轮廓点数     1361
print("points of subsample:", subPoints.shape[0])  # 降采样轮廓点数 34
# 绘制简化轮廓图像
subContour = np.zeros(gray.shape[:2], np.uint8)  # 初始化简化轮廓图像
[cv2.circle(subContour, point, 1, 160, -1) for point in cntPoints]  # 绘制初始轮廓的采样点
[cv2.circle(subContour, point, 4, 255, -1) for point in subPoints]  # 绘制降采样轮廓的采样点
cv2.polylines(subContour, [subPoints], True, 255, thickness=2)  # 绘制多边形，闭合曲线
# 生成 Freeman 链码
cntPoints = np.squeeze(cnt)  # 删除维度为1 的数组维度，(1361,1,2)->(1361,2)
pointsLoop = np.append(cntPoints, [cntPoints[0]], axis=0)  # 首尾循环，结尾添加 cntPoints[0]
chainCode = FreemanChainCode(pointsLoop, gridsep=1)  # 自定义函数，生成链码 (1361,)
print("Freeman chain code:", chainCode.shape)  # 链码长度为轮廓长度 1361
subPointsLoop = np.append(subPoints, [subPoints[0]], axis=0)  # 首尾循环，(34,2)->(35,2)
subChainCode = FreemanChainCode(subPointsLoop, gridsep=50)  # 自定义函数，生成链码 (34,)
print("Down-sampling Freeman chain code:", subChainCode.shape)  # 链码长度为简化轮廓程度 34
print("youcans code:", subChainCode) # [4 2 4 2 2 4 2 2 2 2 2 0 2 0 0 0 2 0 0 6 0 6 6 6 6 6 6 6 6 4 6 4 4 4]
show_images([img,blur,binary,imgCnts,maxContour,subContour])

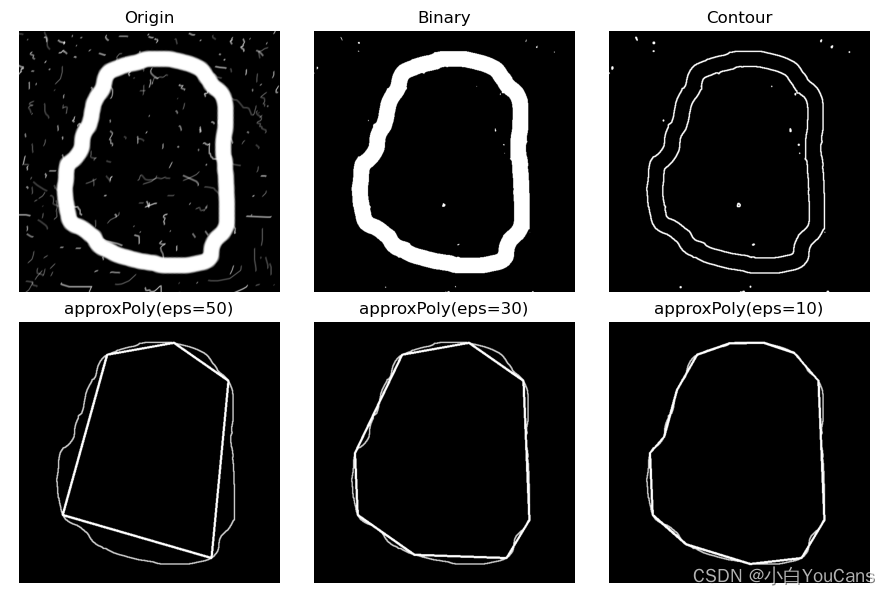
目标轮廓的多边形拟合？

原理：1）在曲线的起点 A 和终点 B 之间做一条直线 AB，是曲线的弦；2）寻找曲线上离该直线段距离最大的点 C，计算其与 AB 的距离 d；3）比较距离 d 与设定的阈值 threshold，如果小于设定阈值则该直线段作为曲线的近似；4）如果距离 d 大于设定阈值，则以 C 点将曲线 AB 分为两段 AC 和 BC，并分别对这两段进行以上步骤的处理；5）当所有曲线都处理完毕时，依次连接所有分割点形成的折线，作为曲线的近似

OpenCV 中的函数 cv.approxPolyDP () 可以用于对图像轮廓点进行多边形拟合

img = cv2.imread("../images/Fig1105.tif", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 灰度图像
blur = cv2.boxFilter(gray, -1, (5, 5))  # 盒式滤波器，9*9 平滑核
_, binary = cv2.threshold(blur, 205, 255, cv2.THRESH_OTSU + cv2.THRESH_BINARY)
# 寻找二值化图中的轮廓
contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)  # OpenCV4~
print('len:', len(contours))
# 绘制全部轮廓，contourIdx=-1 绘制全部轮廓
imgCnts = np.zeros(gray.shape[:2], np.uint8)  # 绘制轮廓函数会修改原始图像
imgCnts = cv2.drawContours(imgCnts, contours, -1, (255, 255, 255), thickness=2)  # 绘制全部轮廓
show_images([img,binary,imgCnts])
cnts = sorted(contours, key=cv2.contourArea, reverse=True)  # 所有轮廓按面积排序
cnt = cnts[0]  # 第 0 个轮廓，面积最大的轮廓，(664, 1, 2)
eps = [50, 30, 10]
for i in range(len(eps)):
	polyFit = cv2.approxPolyDP(cnt, eps[i], True)
	print("eps={}, shape of fitting polygon:{}".format(eps[i], polyFit.shape[0]))
	fitContour = np.zeros(gray.shape[:2], np.uint8)  # 初始化最大轮廓图像
	cv2.polylines(fitContour, [cnt], True, 205, thickness=2)  # 绘制最大轮廓，多边形曲线
	cv2.polylines(fitContour, [polyFit], True, 255, 3)
	show_images([fitContour])

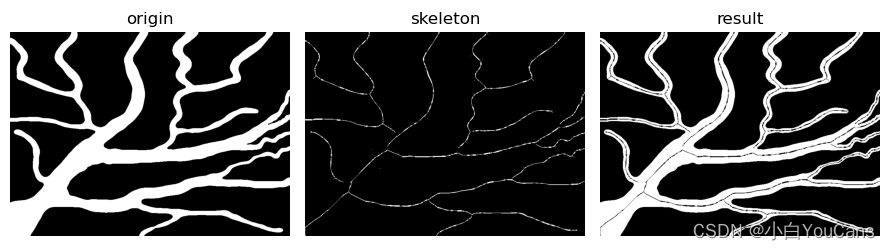
目标轮廓的骨架提取？

骨架可以由区域的边界计算。提取骨架的常用方法是用重建开运算来实现，在保持端点和线的连通性的同时持续细化目标区域

img = cv2.imread("../images/bloodvessels.tif", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 灰度图像
_, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_OTSU + cv2.THRESH_BINARY)
dst = binary.copy()
skeleton = np.zeros(gray.shape, np.uint8)  # 创建空骨架图
kernel = cv2.getStructuringElement(cv2.MORPH_CROSS, (5, 5))
while (True):
	dst = cv2.erode(dst, kernel, None, None, 1)  # 腐蚀
	opening = cv2.morphologyEx(dst, cv2.MORPH_OPEN, kernel)  # 开运算
	subSkeleton = cv2.subtract(dst, opening)  # 获得骨架子集
	skeleton = cv2.bitwise_or(skeleton, subSkeleton)  # 将删除的像素添加到骨架图
	if cv2.countNonZero(dst) == 0:
		break
show_images([img,skeleton,result])

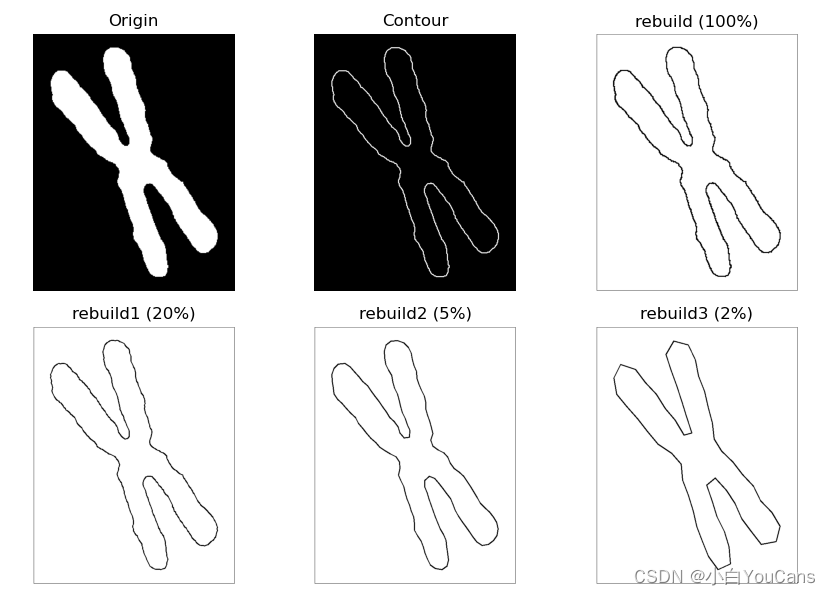
目标轮廓的傅里叶描述子？

傅里叶描述子的基本思想是用目标边界曲线的傅里叶变换来描述目标区域的形状，将二维描述问题简化为一维描述问题。傅里叶描述子具有旋转、平移和尺度不变性

由于傅里叶变换的低频分量决定整体形状，高频分量决定形状的细节。因此，仅取前 P 个系数相当于保留低频系数、删除高频系数的理想低通滤波器进行滤波。用少量低频的傅里叶描述子就可以描述目标边界曲线形状的基本特征。下面的例程表明，使用约 1% 的傅里叶描述子，就可以较好地描述边界曲线的基本形状

def truncFFT(fftCnt, pLowF=64):  # 截短傅里叶描述子
	fftShift = np.fft.fftshift(fftCnt)  # 中心化，将低频分量移动到频域中心
	center = int(len(fftShift)/2)
	low, high = center - int(pLowF/2), center + int(pLowF/2)
	fftshiftLow = fftShift[low:high]
	fftLow = np.fft.ifftshift(fftshiftLow)  # 逆中心化
	return fftLow
def reconstruct(img, fftCnt, scale, ratio=1.0):  # 由傅里叶描述子重建轮廓图
	pLowF = int(fftCnt.shape[0] * ratio)  # 截短长度 P<=K
	fftLow = truncFFT(fftCnt, pLowF)  # 截短傅里叶描述子，删除高频系数
	ifft = np.fft.ifft(fftLow)  # 傅里叶逆变换 (P,)
	cntRebuild = np.stack((ifft.real, ifft.imag), axis=-1)  # 复数转为数组 (P, 2)
	if cntRebuild.min() < 0:
		cntRebuild -= cntRebuild.min()
	cntRebuild *= scale / cntRebuild.max()
	cntRebuild = cntRebuild.astype(np.int32)
	print("ratio={}, fftCNT:{}, fftLow:{}".format(ratio, fftCnt.shape, fftLow.shape))
	rebuild = np.ones(img.shape, np.uint8)*255  # 创建空白图像
	cv2.rectangle(rebuild, (2,3), (568,725), (0,0,0), )  # 绘制边框
	cv2.polylines(rebuild, [cntRebuild], True, 0, thickness=2)  # 绘制多边形，闭合曲线
	return rebuild
# 特征提取之傅里叶描述子
img = cv2.imread("../images/chromosome.tif", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 灰度图像
_, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_OTSU + cv2.THRESH_BINARY)
# 寻找二值化图中的轮廓，method=cv2.CHAIN_APPROX_NONE 输出轮廓的每个像素点
contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)  # OpenCV4~
cnts = sorted(contours, key=cv2.contourArea, reverse=True)  # 所有轮廓按面积排序
cnt = cnts[0]  # 第 0 个轮廓，面积最大的轮廓，(664, 1, 2)
cntPoints = np.squeeze(cnt)  # 删除维度为 1 的数组维度，(2867, 1, 2)->(2867,2)
lenCnt = cnt.shape[0]  # 轮廓点的数量
imgCnts = np.zeros(gray.shape[:2], np.uint8)  # 创建空白图像
cv2.drawContours(imgCnts, cnt, -1, (255, 255, 255), 2)  # 绘制轮廓
# 离散傅里叶变换，生成傅里叶描述子 fftCnt
cntComplex = np.empty(cntPoints.shape[0], dtype=complex)  # 声明复数数组 (2867,)
cntComplex = cntPoints[:,0] + 1j * cntPoints[:,1]  # (xk,yk)->xk+j*yk
fftCnt = np.fft.fft(cntComplex)  # 离散傅里叶变换，生成傅里叶描述子
# 由全部傅里叶描述子重建轮廓曲线
scale = cntPoints.max()  # 尺度系数
rebuild = reconstruct(img, fftCnt, scale)  # 傅里叶逆变换重建轮廓曲线，傅里叶描述子 (2866,)
# 由截短傅里叶系数重建轮廓曲线
rebuild1 = reconstruct(img, fftCnt, scale, ratio=0.2)  # 截短比例 20%，傅里叶描述子 (572,)
rebuild2 = reconstruct(img, fftCnt, scale, ratio=0.05)  # 截短比例 5%，傅里叶描述子 (142,)
rebuild3 = reconstruct(img, fftCnt, scale, ratio=0.02)  # 截短比例 2%，傅里叶描述子 (56,)
show_images([img,imgCnts,rebuild,rebuild1,rebuild2,rebuild3])

目标轮廓的紧致度？

紧致度（Compactness），周长的平方与面积之比，具有平移、尺度、旋转不变性

n = 4
for i in range(1,n+1):
	path = "../images/wingding{}.tif".format(str(i))
	gray = cv2.imread(path, flags=0)
	_, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
	contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)  # OpenCV4~
	cnts = sorted(contours, key=cv2.contourArea, reverse=True)  # 所有轮廓按面积排序
	cnt = cnts[0]  # 第 0 个轮廓，面积最大的轮廓，(2867, 1, 2)
	print("{}, path:{}, shape:{}".format(i, path, gray.shape))
	area = cv2.contourArea(cnt)  # 轮廓面积 (area)
	print("\tarea of contour: ", area)
	perimeter = cv2.arcLength(cnt, True)  # 轮廓周长 (perimeter)
	print("\tperimeter of contour: {:.1f}".format(perimeter))
	compact = perimeter ** 2 / area  # 轮廓的紧致度 (compactness)

目标轮廓的圆度？

圆度（circularity），面积与周长的平方之比，具有平移、尺度、旋转不变性

n = 4
for i in range(1,n+1):
	path = "../images/wingding{}.tif".format(str(i))
	gray = cv2.imread(path, flags=0)
	_, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
	contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)  # OpenCV4~
	cnts = sorted(contours, key=cv2.contourArea, reverse=True)  # 所有轮廓按面积排序
	cnt = cnts[0]  # 第 0 个轮廓，面积最大的轮廓，(2867, 1, 2)
	area = cv2.contourArea(cnt)  # 轮廓面积 (area)
	print("\tarea of contour: ", area)
	perimeter = cv2.arcLength(cnt, True)  # 轮廓周长 (perimeter)
	print("\tperimeter of contour: {:.1f}".format(perimeter))
	circular = 4 * np.pi * area / perimeter ** 2  # 轮廓的圆度 (circularity)
	print("\tcircularity of contour: {:.2f}".format(circular))

目标轮廓的偏心率？

偏心率（Eccentricity），椭圆的偏心率定义为焦距与椭圆长轴的长度之比

n = 4
for i in range(1,n+1):
	path = "../images/wingding{}.tif".format(str(i))
	gray = cv2.imread(path, flags=0)
	_, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
	contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)  # OpenCV4~
	cnts = sorted(contours, key=cv2.contourArea, reverse=True)  # 所有轮廓按面积排序
	cnt = cnts[0]  # 第 0 个轮廓，面积最大的轮廓，(2867, 1, 2)
	ellipse = cv2.fitEllipse(cnt)  # 轮廓的拟合椭圆
	# 椭圆中心点 (x,y), 长轴短轴长度 (a,b), 旋转角度 ang
	(x, y), (a, b), ang = np.int32(ellipse[0]), np.int32(ellipse[1]), round(ellipse[2], 1)
	# print("Fitted ellipse: (Cx,Cy)={}, (a,b)={}, ang={})".format((x, y), (a, b), ang))
	# 轮廓的偏心率 (eccentricity)
	if (a > b):
		eccentric = np.sqrt(1.0 - (b / a) ** 2)  # a 为长轴
	else:
		eccentric = np.sqrt(1.0 - (a / b) ** 2)
	print("\teccentricity of contour: {:.2f}".format(eccentric))

目标区域 “区域特征”？

针对目标所在区域的特征描述符（Region descriptors），称为区域特征描述子

目标区域的 “纹理特征”？

纹理体现了物体表面的具有缓慢变化或者周期性变化的表面结构组织排列属性。纹理特征描述了图像或图像区域所对应景物的表面性质
纹理与尺度密切相关，一般仅呈现在特定尺度上，对纹理的识别要在恰当的尺度上进行。纹理特征不是基于像素点的特征，而是一种基于像素区域的统计特性。因此，纹理能用来描述不同的图像区域
纹理特征通常具有旋转不变性，在模式匹配中对噪声有较强的抵抗能力。描述图像中的纹理区域，要基于区域尺度、可分辨灰度元素的数目以及这些灰度元素的相互关系等。

目标区域的 “LBP 纹理特征算子”？

局部二值模式是一种用来描述图像局部纹理特征的算子，它具有旋转不变性和灰度不变性的优点。LBP 算子利用了邻域点的量化关系，可以有效地消除光照对图像的影响。只要光照变化不足以改变相邻像素点的像素值的大小关系，LBP 算子的值就不会发生变化

原始的 LBP 算子定义在 3×3 的窗口内，以窗口中心像素为阈值，与相邻的 8 个像素的灰度值比较，大于阈值则标记为 1，否则标记为 0。从右上角开始顺时针旋转，排列 8 个 0/1 标记值，得到一个 8 位二进制数，就是窗口中心像素点的 LBP 值

def getLBP1(gray):
	height, width = gray.shape
	dst = np.zeros((height, width), np.uint8)
	kernel = np.array([1, 2, 4, 128, 0, 8, 64, 32, 16]).reshape(3,3)  # 从左上角开始顺时针旋转
	# kernel = np.array([64,128,1,32,0,2,16,8,4]).reshape(3,3)  # 从右上角开始顺时针旋转
	for h in range(1, height-1):
		for w in range(1, width-1):
			LBPMat = (gray[h-1:h+2, w-1:w+2] >= gray[h, w])  # 阈值比较
			dst[h, w] = np.sum(LBPMat * kernel)  # 二维矩阵相乘
	return dst
def getLBP2(gray):
	height, width = gray.shape
	dst = np.zeros((height, width), np.uint8)
	# kernelFlatten = np.array([1, 2, 4, 128, 0, 8, 64, 32, 16])  # 从左上角开始顺时针旋转
	kernelFlatten = np.array([64,128,1,32,0,2,16,8,4])  # 从右上角开始顺时针旋转
	for h in range(1, height-1):
		for w in range(1, width-1):
			LBPFlatten = (gray[h-1:h+2, w-1:w+2] >= gray[h, w]).flatten()  # 展平为一维向量, (9,)
			dst[h, w] = np.vdot(LBPFlatten, kernelFlatten)  # 一维向量的内积
	return dst
def getLBP3(gray):
	height, width = gray.shape
	dst = np.zeros((height, width), np.uint8)
	for h in range(1, height-1):
		for w in range(1, width-1):
			center = gray[h, w]
			code = 0  # 从左上角开始顺时针旋转
			code |= (gray[h-1, w-1] >= center) << (np.uint8)(7)
			code |= (gray[h-1, w  ] >= center) << (np.uint8)(6)
			code |= (gray[h-1, w+1] >= center) << (np.uint8)(5)
			code |= (gray[h  , w+1] >= center) << (np.uint8)(4)
			code |= (gray[h+1, w+1] >= center) << (np.uint8)(3)
			code |= (gray[h+1, w  ] >= center) << (np.uint8)(2)
			code |= (gray[h+1, w-1] >= center) << (np.uint8)(1)
			code |= (gray[h  , w-1] >= center) << (np.uint8)(0)
			dst[h, w] = code
	return dst
# 原始 LBP 算法：选取中心点周围的 8个像素点，阈值处理后标记为 8位二进制数
img = cv2.imread("../images/fabric1.png", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 灰度图像
# 1) 二重循环, 二维矩阵相乘
timeBegin = cv2.getTickCount()
imgLBP1 = getLBP1(gray)  # # 从左上角开始顺时针旋转
timeEnd = cv2.getTickCount()
time = (timeEnd-timeBegin)/cv2.getTickFrequency()
print("1) 二重循环, 二维矩阵相乘:", round(time, 4))
# 2) 二重循环, 一维向量的内积
timeBegin = cv2.getTickCount()
imgLBP2 = getLBP2(gray)  # 从右上角开始顺时针旋转
timeEnd = cv2.getTickCount()
time = (timeEnd-timeBegin)/cv2.getTickFrequency()
print("2) 二重循环, 一维向量的内积:", round(time, 4))
# 3) 二重循环, 按位操作
timeBegin = cv2.getTickCount()
imgLBP3 = getLBP3(gray)  # 从右上角开始顺时针旋转
timeEnd = cv2.getTickCount()
time = (timeEnd-timeBegin)/cv2.getTickFrequency()
print("3) 二重循环, 按位操作:", round(time, 4))
# 4) skimage 特征检测
from skimage.feature import local_binary_pattern
timeBegin = cv2.getTickCount()
lbpSKimage = local_binary_pattern(gray, 8, 1)
timeEnd = cv2.getTickCount()
time = (timeEnd-timeBegin)/cv2.getTickFrequency()
print("4) skimage.feature 封装:", round(time, 4))

目标区域的 “extendLBP 纹理特征算子”？

基本的 LBP 纹理特征描述子只覆盖了一个固定半径范围内的小区域。这种特征描述方法是随尺度变化的，当图像尺度变化时 LBP 特征编码也会发生变化，因此在大尺寸图像时就不能准确提取到所需的纹理特征，不能反映所描述的纹理信息

为了满足尺度、灰度和旋转不变性的要求，Ojala 等对 LBP 算子进行了改进，将 3×3 邻域扩展到任意邻域，并用圆形邻域代替了方形邻域。改进算子允许在半径为 R 的圆形邻域内有 P 个采样点，称为扩展 LBP 算子（Extended LBP）

def basicLBP(gray):
	height, width = gray.shape
	dst = np.zeros((height, width), np.uint8)
	kernelFlatten = np.array([1, 2, 4, 128, 0, 8, 64, 32, 16])  # 从左上角开始顺时针旋转
	for h in range(1, height-1):
		for w in range(1, width-1):
			LBPFlatten = (gray[h-1:h+2, w-1:w+2] >= gray[h, w]).flatten()  # 展平为一维向量, (9,)
			dst[h, w] = np.vdot(LBPFlatten, kernelFlatten)  # 一维向量的内积
	return dst
# extend LBP，在半径为 R 的圆形邻域内有 N 个采样点
def extendLBP(gray, r=3, n=8):
	height, width = gray.shape
	ww = np.empty((n, 4), np.float)  # (8,4)
	p = np.empty((n, 4), np.int)  # [x1, y1, x2, y2]
	for k in range(n):  # 双线性插值估计坐标偏移量和权值
		# 计算坐标偏移量 rx，ry
		rx = r * np.cos(2.0 * np.pi * k / n)
		ry = -(r * np.sin(2.0 * np.pi * k / n))
		# 对采样点分别进行上下取整
		x1, y1 = int(np.floor(rx)), int(np.floor(ry))
		x2, y2 = int(np.ceil(rx)), int(np.ceil(ry))
		# 将坐标偏移量映射到 0-1
		tx = rx - x1
		ty = ry - y1
		# 计算插值的权重
		ww[k, 0] = (1 - tx) * (1 - ty)
		ww[k, 1] = tx * (1 - ty)
		ww[k, 2] = (1 - tx) * ty
		ww[k, 3] = tx * ty
		p[k, 0], p[k, 1], p[k, 2], p[k, 3] = x1, y1, x2, y2
	dst = np.zeros((height-2*r, width-2*r), np.uint8)
	for h in range(r, height-r):
		for w in range(r, width-r):
			center = gray[h, w]  # 中心像素点的灰度值
			for k in range(n):
				# 双线性插值估计采样点 k 的灰度值
				# neighbor = gray[i+y1,j+x1]*w1 + gray[i+y2,j+x1]*w2 + gray[i+y1,j+x2]*w3 + gray[i+y2,j+x2]*w4
				x1, y1, x2, y2 = p[k,0], p[k,1], p[k,2], p[k,3]
				gInterp = np.array([gray[h+y1,w+x1], gray[h+y2,w+x1], gray[h+y1,w+x2], gray[h+y2,w+x2]])
				wFlatten = ww[k,:]
				grayNeighbor = np.vdot(gInterp, wFlatten)  # 一维向量的内积
				# 由 N 个采样点与中心像素点的灰度值比较，构造 LBP 特征编码
				dst[h-r, w-r] |= (grayNeighbor > center) << (np.uint8)(n-k-1)
	return dst
# 特征描述之 extendLBP 改进算子
img = cv2.imread("../images/fabric1.png", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 灰度图像
# 1) skimage 特征检测
from skimage.feature import local_binary_pattern
timeBegin = cv2.getTickCount()
lbpSKimage = local_binary_pattern(gray, 8, 1)
imgLBP1 = basicLBP(gray)  # 从右上角开始顺时针旋转
r1, n1 = 3, 8
imgLBP2 = extendLBP(gray, r1, n1)
r2, n2 = 5, 8
imgLBP3 = extendLBP(gray, r2, n2)
show_images([img,gray,lbpSKimage,imgLBP1,imgLBP2,imgLBP3])

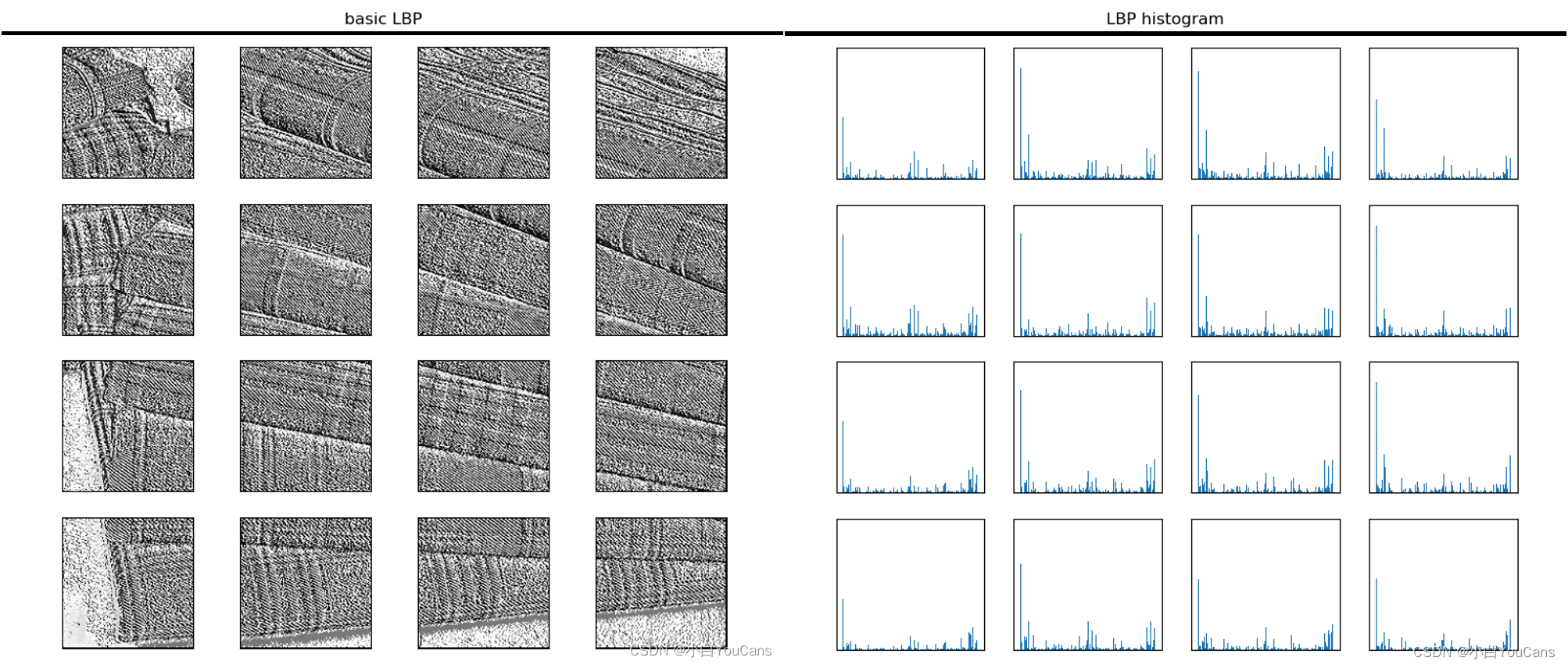
目标区域的 “LBP 直方图”？

图像可以用 LBP 特征向量来表示，但在应用中一般并不是直接使用 LBP 图谱进行分类识别，而是使用 LBP 特征谱的统计直方图进行分类识别。因为 LBP 特征是与图像中的位置紧密相关的，直接对两幅图片提取 LBP 特征进行判别分析，会由于位置没有对准而带来很大的误差

为了解决这个问题，可以将图像划分为若干子区域，对每个子区域内提取 LBP 特征后在子区域内建立 LBP 特征的统计直方图。图片的每个子区域可以用一个统计直方图来描述，整个图片就由若干个统计直方图组成，称为 LBP 特征的统计直方图

def basicLBP(gray):
	height, width = gray.shape
	dst = np.zeros((height, width), np.uint8)
	kernelFlatten = np.array([1, 2, 4, 128, 0, 8, 64, 32, 16])  # 从左上角开始顺时针旋转
	for h in range(1, height-1):
		for w in range(1, width-1):
			LBPFlatten = (gray[h-1:h+2, w-1:w+2] >= gray[h, w]).flatten()  # 展平为一维向量, (9,)
			dst[h, w] = np.vdot(LBPFlatten, kernelFlatten)  # 一维向量的内积
	return dst
def calLBPHistogram(imgLBP, nCellX, nCellY):  # 计算 LBP 直方图
	height, width = gray.shape
	# nCellX, nCellY = 4, 4  # 将图像划分为 nCellX*nCellY 个子区域
	hCell, wCell = height//nCellY, width//nCellX  # 子区域的高度与宽度 (150,120)
	LBPHistogram = np.zeros((nCellX*nCellY, 256), np.int)
	for j in range(nCellY):
		for i in range(nCellX):
			cell = imgLBP[j * hCell:(j + 1) * hCell, i * wCell:(i + 1) * wCell].copy()  # 子区域 cell LBP
			print("{}, Cell({}{}): [{}:{}, {}:{}]".format
				  (j*nCellX+i+1, j+1, i+1, j*hCell, (j+1)*hCell, i*wCell, (i+1)*wCell))
			histCell = cv2.calcHist([cell], [0], None, [256], [0, 256])  # 子区域 LBP 直方图
			LBPHistogram[(i+1)*(j+1)-1, :] = histCell.flatten()
	print(LBPHistogram.shape)
	return LBPHistogram
# 特征描述之 LBP 直方图
img = cv2.imread("../images/fabric2.png", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 灰度图像
height, width = gray.shape
nCellX, nCellY = 4, 4  # 将图像划分为 nCellX*nCellY 个子区域
hCell, wCell = height//nCellY, width//nCellX  # 子区域的高度与宽度 (150,120)
print("img: h={},w={}, cell: h={},w={}".format(height, width, hCell, wCell))
basicLBP = basicLBP(gray)  # 计算 basicLBP 特征算子
# LBPHistogram = calLBPHistogram(basicLBP, nCellX, nCellY)  # 计算 LBP 直方图 (16, 256)
for j in range(nCellY):
	for i in range(nCellX):
		cell = basicLBP[j*hCell:(j+1)*hCell, i*wCell:(i+1)*wCell].copy()  # 子区域 cell LBP
		histCV = cv2.calcHist([cell], [0], None, [256], [0, 256])  # 子区域 cell LBP 直方图
		ax1 = fig1.add_subplot(nCellY, nCellX, j * nCellX + i + 1)
		ax1.set_xticks([]), ax1.set_yticks([])
		ax1.imshow(cell, 'gray')  # 绘制子区域 LBP  
		ax2 = fig2.add_subplot(nCellY,nCellX,j*nCellX+i+1)
		ax2.set_xticks([]), ax2.set_yticks([])
		ax2.bar(range(256), histCV[:, 0])  # 绘制子区域 LBP 直方图
		print("{}, Cell({}{}): [{}:{}, {}:{}]".format
			  (j * nCellX + i + 1, j + 1, i + 1, j * hCell, (j + 1) * hCell, i * wCell, (i + 1) * wCell))

目标区域的灰度共生矩阵 (GLCM)?

灰度共生矩阵（Gray level co-occurrence matrix，GLCM）是特征检测与分析的重要方法，在纹理分析、特征分类、图像质量评价中应用广泛
图像的像素具有不同的灰度级，灰度共生矩阵表示不同灰度组合同时出现的频率。简单地说，灰度共生矩阵反映灰度图像中某种形状的像素对在整个图像中出现的次数

灰度共生矩阵的数据量很大，一般不直接用它来描述纹理特征，而是构建一些统计量作为纹理分类特征。例如，能量、熵、对比度、均匀性、相关性、方差等

from skimage.feature import greycomatrix, greycoprops
img = cv2.imread("../images/fabric1.png", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 灰度图像
height, width = gray.shape
table16 = np.array([(i//16) for i in range(256)]).astype("uint8")  # 16 levels
gray16 = cv2.LUT(gray, table16)  # 灰度级压缩为 [0,15]
# 计算灰度共生矩阵 GLCM
dist = [1, 4]  # 计算 2 个距离偏移量 [1, 2]
degree = [0, np.pi/4, np.pi/2, np.pi*3/4]  # 计算 4 个方向
glcm = greycomatrix(gray16, dist, degree, levels=16)  # 灰度级 L=16
print(glcm.shape)  # (16,16,2,4)
# 由灰度共生矩阵 GLCM 计算特征统计量
for prop in ['contrast', 'dissimilarity','homogeneity', 'energy', 'correlation', 'ASM']:
	feature= greycoprops(glcm, prop).round(4)  # (2,4)
	print("{}: {}".format(prop, feature))

目标区域纹理特征的频谱方法？

傅里叶谱可以描述图像中的周期性或半周期性二维模式的方向性，因此可以基于傅里叶变换对纹理进行频谱分析
纹理与图像频谱中的高频分量密切相关，纹理模式在频谱图表现为高能量的爆发

目标区域特征的矩不变量？

图像矩是对特征进行参数描述的一种算法，通常描述了图像形状的全局特征，并提供了大量的关于该图像不同类型的几何特性信息，比如大小、位置、方向及形状等

Hu 利用二阶和三阶归一化中心距构造了 7 个不变矩 M1~M7，在连续图像下具有平移、灰度、尺度、旋转不变性，是高度浓缩的图像特征。不变矩能够描述图像的整体性质，从而在边缘提取、图像匹配及目标识别中得到了广泛的应用

gray = cv2.imread("../images/Fig1137.tif", flags=0)  # 灰度图像
height, width = gray.shape  # (568, 568)
# 图像的平移，缩放，旋转和镜像
grayList = []
grayList.append(gray)  # [0]，原始图像
mat = np.float32([[1, 0, 50], [0, 1, 50]])
grayList.append(cv2.warpAffine(gray, mat, (height, width)))  # [1]，图像平移
top, bottom, left, right = height//4, height//4, width//4, width//4
grayResize = cv2.resize(gray, (width//2, height//2))  # 图像缩放 (284, 284)
replicate = cv2.copyMakeBorder(grayResize, top, bottom, left, right, cv2.BORDER_CONSTANT, value=0)
grayList.append(replicate)  # [2]，图像缩放并填充至原来尺寸 (568, 568)
grayList.append(cv2.flip(gray, 1))  # [3]，图像镜像，水平翻转
mar = cv2.getRotationMatrix2D((width//2, height//2), angle=45, scale=1)  # 图像中心作为旋转中心
rotate = cv2.warpAffine(gray, mar, (height, width))  # 旋转变换，默认为黑色填充
grayList.append(rotate)  # [4]，图像旋转 45度
grayList.append(cv2.rotate(gray, cv2.ROTATE_90_COUNTERCLOCKWISE))  # [5]，图像逆时针旋转90度
plt.figure(figsize=(9, 6))
for i in range(len(grayList)):
	moments = cv2.moments(grayList[i])  # 返回几何矩 mpq, 中心矩 mupq 和归一化矩 nupq
	huM = cv2.HuMoments(moments)  # 计算 Hu 不变矩
	plt.subplot(2,3,i+1), plt.axis('off'), plt.imshow(grayList[i], 'gray')
	# print("Moments of gray:\n", moments)
	print("HuMoments of gray:\n", np.log10(np.abs(huM.T)).round(4))
plt.show()

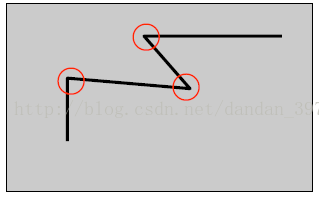
什么是角点？

角点的定义很多，可以指一阶导数 (即灰度的梯度) 的局部最大所对应的像素点，也可以指两条及两条以上边缘的交点
角点检测算法基本思想是使用一个固定窗口（取某个像素的一个邻域窗口）在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，窗口中的像素灰度变化程度，如果存在任意方向上的滑动，都有着较大灰度变化，那么我们可以认为该窗口中存在角点
角点可以应用三维场景重建运动估计，目标跟踪、目标识别、图像配准与匹配等计算机视觉领域

OpenCV 的 Harris 角点检测算法？

在基于灰度变换的角点检测算法中，Harris 算法重复性良好、检测效率较高，应用较为广泛。Harris 的原理是，通过检测窗口在图像上移动，计算移动前后窗口中像素的灰度变化。角点是两条边的交点，其特征是检测窗口沿任意方向移动都会导致灰度的显著变化

img = cv2.imread("../images/Chess01.png", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # (600, 540)
blockSize = [2, 3, 5]  # 滑动窗口大小
ksize = [3, 5, 9]  # Sobel 核函数大小
plt.figure(figsize=(9, 9))
for i in range(len(blockSize)):
	for j in range(len(ksize)):
		dst = cv2.cornerHarris(gray, blockSize[i], ksize[j], k=0.04)
		imgCorner = np.copy(img)
		imgCorner[dst > 0.01*dst.max()] = [0, 0, 255]  # 筛选角点，红色标记
		show_images([imgCorner])

OpenCV 的 Harris 角点检测之精确定位？

OpenCV 提供了函数 cv.cornerSubPix () 用于细化角点位置，细化了以亚像素精度检测到的角点位置

img = cv2.imread("../images/sign01.png", flags=1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # (600, 540)
print(img.shape)  # (600, 836, 3)
# 角点检测
gray = np.float32(gray)    # uint8，float32 都支持
dst = cv2.cornerHarris(gray, 2, 3, 0.04)  # Harris 角点检测
_, dst = cv2.threshold(dst, 0.01 * dst.max(), 255, 0)  # 提取角点
dst = np.uint8(dst)  # (600, 836)
# 角点检测结果图像
imgCorner = np.copy(img)
imgCorner[:,:,2] = cv2.bitwise_or(imgCorner[:,:,2], dst)  # 筛选角点，红色标记
# 对检测角点进行精细定位
ret, labels, stats, centroids = cv2.connectedComponentsWithStats(dst)  # 检测连通区域
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 100, 0.001)  # 终止判据
fineCorners = cv2.cornerSubPix(gray, np.float32(centroids), (5,5), (-1,-1), criteria)  # (144, 2)
# 精细定位检测图像
imgFineCorners = np.copy(img)
centroids = centroids.astype(np.int)  # 连通区域的质心 (x,y)
fineCorners = fineCorners.astype(np.int)  # 精细定位的角点 (x,y)
imgFineCorners[centroids[:, 1], centroids[:, 0]] = [0,255,0]  # Harris 检测位置，绿色
imgFineCorners[fineCorners[:, 1], fineCorners[:, 0]] = [0,0,255]  # 精细检测位置，红色
show_images([img,imgCorner,imgFineCorners])

OpenCV 的 Shi-Tomasi 角点检测算法？

Shi-Tomas 算法是对 Harris 角点检测算法的改进，一般会比 Harris 算法得到更好的角点

函数 cv. goodFeaturesToTrack 通过 Shi-Tomasi 方法找出图像中最突出的 N 个角点

img = cv2.imread("../images/sign04.png", flags=1)  # (300, 300, 3)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Harris 检测角点
dst = cv2.cornerHarris(gray, 2, 3, k=0.04)
# Harris[dst > 0.01*dst.max()] = [0, 0, 255]  # 筛选角点，红色标记
corners = np.column_stack(np.where(dst>0.1*dst.max()))  # 筛选并返回角点坐标 (y,x)
corners = corners.astype(np.int)  # 检测到的角点的点集 (y,x), (92, 2)
imgHarris = np.copy(img)
for point in corners:  # 注意坐标次序
	cv2.circle(imgHarris, (point[1], point, 4, (0,0,255), 2)  # # 在点 (x,y) 处画圆
# Shi-tomas 检测角点
corners = cv2.goodFeaturesToTrack(gray, 30, 0.3, 5)  # (30, 1, 2)
corners = np.squeeze(corners).astype(np.int)  # (30, 1, 2)->(30,2)  角点坐标 (x,y)
imgShiTomas = np.copy(img)
for point in corners:
	cv2.circle(imgShiTomas, point, 4, (0,0,255), 2)  # # 在点 (x,y) 处画圆
show_images([img,imgHarris,imgShiTomas])

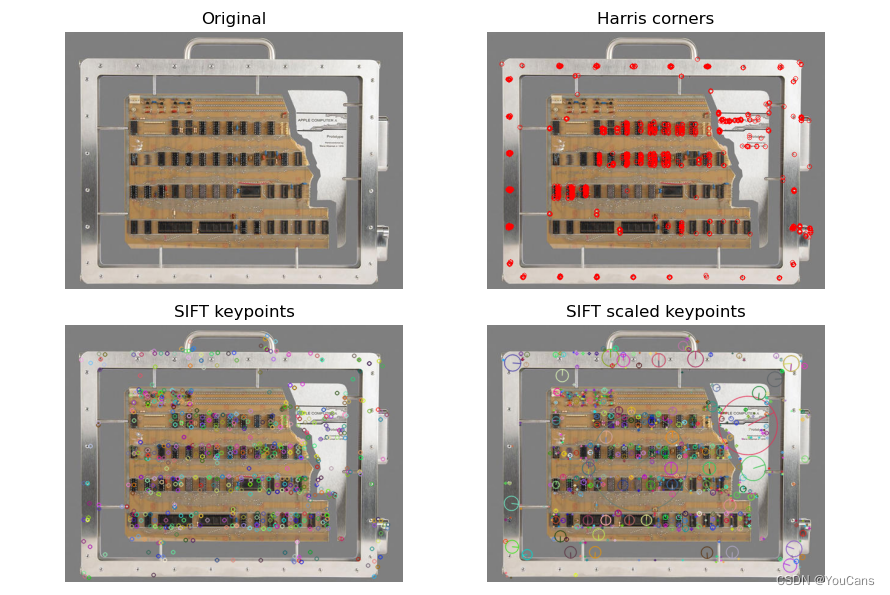
尺度不变特征转换算法（SIFT）特征点检测算法？

SIFT 算法的实质是在不同的尺度空间上查找关键点（特征点），计算特征点的大小、方向、尺度信息，利用这些信息组成关键点对特征点进行描述的问题。SIFT 算法查找的关键点都是高度显著且容易获取的 “稳定” 特征点，如角点、边缘点、暗区的亮点以及亮区的暗点等，这些特征与大小、旋转无关，对于光线、噪声、视角改变的鲁棒性也很高
（1）尺度空间极值检测：通过高斯差分金字塔识别潜在的对于尺度和旋转不变的兴趣点
（2）关键点的精确定位：通过模型拟合确定关键点位置和尺度
（3）确定关键点的方向：基于图像局部的梯度方向，确定每个关键点的一个或多个方向
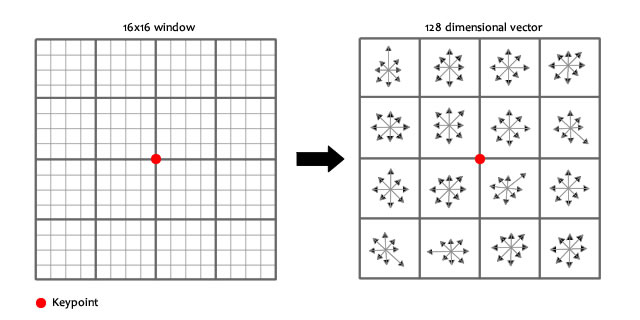
（4）关键点描述：在关键点的邻域内，在选定的尺度上测量图像局部的梯度。计算关键点周围 16 x 16 区域的梯度，分为 4 x 4 个子 grid 处理，每个 grid 计算 8 个方向的梯度，最终得到 4 x 4 x 8=128

基于 SIFI 特征图像匹配算法？

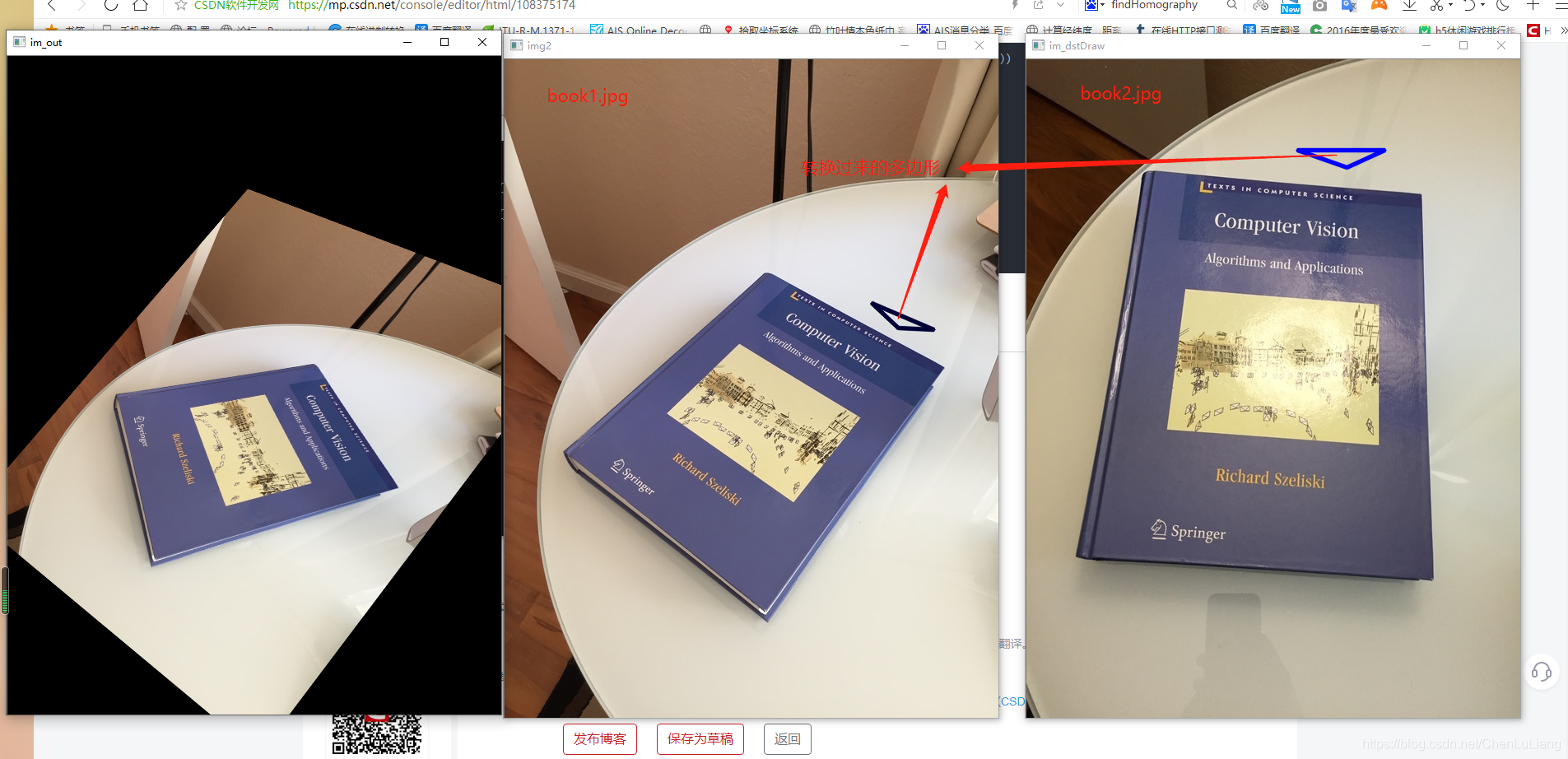
获取图像的尺度不变特征的关键点信息，每个关键由 128 维长度的特征描述，通过计算所有关键点的距离，完成关键点的匹配。上图是完成关键点匹配后，拿出 4 对匹配的关键点进行透视变换

im_src = cv2.imread('book2.jpg')
pts_src = np.array([[141, 131], [480, 159], [493, 630],[64, 601]])
im_dst = cv2.imread('book1.jpg')
pts_dst = np.array([[318, 256],[534, 372],[316, 670],[73, 473]])
#自定义画一个多边形 测试投影关系
polyline=[[329,110],[435,110],[389,131]]
im_dstDraw= cv2.polylines(im_src,[np.int32(polyline)] ,True,255,3, cv2.LINE_AA)
cv2.imshow("im_dstDraw", im_dstDraw)
# 计算单应性矩阵 这个是重点
h1, status = cv2.findHomography(pts_src, pts_dst)
#对图像进行透视变换，就是变形 把book1变形匹配book2
im_out = cv2.warpPerspective(im_dst, h1, (im_dst.shape[1],im_dst.shape[0]))
cv2.imshow("im_out", im_out)
#取图片高宽
h,w = im_dst.shape[1],im_dst.shape[0]
pts = np.float32(polyline).reshape(-1,1,2)
#透视变换  是将图片投影到一个新的视平面
dst = cv2.perspectiveTransform(pts,h1)
#绘制变换关系
img2 = cv2.polylines(im_dst,[np.int32(dst)],True,55,3, cv2.LINE_AA)

SURF 特征点检测算法？

SURF 算法的结构框架与 SIFT 类似，基本步骤包括：构造尺度空间、检测关键点、选取主方向和特征描述
（1）基于均值滤波器实现 Hessian 矩阵：SIFT 算法先构造尺度空间检测极值点，再通过 Hessian 矩阵判别并消除不稳定的边缘效应
（2）构造尺度空间：为了获取特征点的尺度参数，可以通过建立图像金字塔构造尺度空间
（3）特征点定位：特征点定位的方法与 SIFT 算法类似
（4）选取关键点的主方向：为了保证特征矢量具有旋转不变形，需要对于每一个特征点分配一个主要方向

（5）构造关键点的特征描述子：SIFT 把关键点的邻域划分为 4x4=16 个子块，每个子块统计 8 个方向的梯度，得到 4x4x8=128 维向量量作为 SIFT 描述子；通过主方向旋转矫正后，SURF 将关键点周围 20s×20s 的邻域划分为 4×4=16 个子块，每个子块 5s×5s 个像素。对每个子块，用尺度为 2S 的 Haar 小波计算水平方向和垂直方向（相对于主方向）的小波响应值，构造 4 维特征向量。将 4×4 个子块的 4 维特征向量 v 组合，形成 64 位的特征向量，就是 SURF 的特征描述符

img = cv.imread("../images/Circuit04.png", flags=1)
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)  # (425, 558)
height, width = gray.shape[:2]
print("shape of image: ", height, width)
# 比较：SIFT 关键点检测
# sift = cv.xfeatures2d.SIFT_create()  # OpenCV 早期版本
sift = cv.SIFT.create()  # sift 实例化对象
kpSift = sift.detect(gray, None)  # 关键点检测，kp 为关键点信息（包括方向）
print("shape of keypoints: ", len(kpSift))  # 775
imgSift1 = cv.drawKeypoints(img, kpSift, None)  # 只绘制关键点位置
imgSift2 = cv.drawKeypoints(img, kpSift, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)  # 绘制关键点大小和方向
# 比较：SURF 关键点检测
surf = cv.xfeatures2d.SURF.create(1000)  # surf 实例化对象
kpSurf, desSurf = surf.detect(gray, None)  # 关键点检测，kp 为关键点信息（包括方向）
print("shape of keypoints: ", len(kpSurf))  # 775
imgSurf1 = cv.drawKeypoints(img, kpSurf, None)  # 只绘制关键点位置
imgSurf2 = cv.drawKeypoints(img, kpSurf, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)  # 绘制关键点大小和方向
show_images([imgSift1,imgSift2,imgSurf1,imgSurf2])

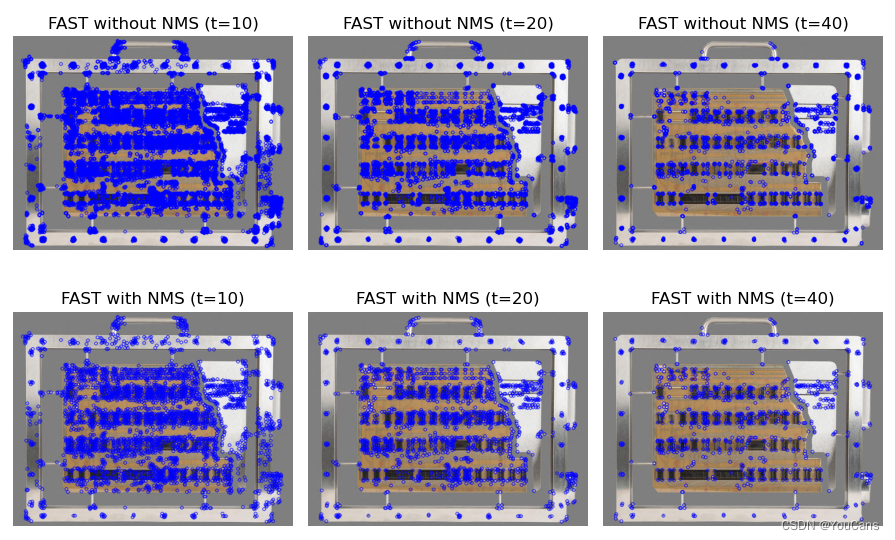
FAST 特征点检测算法？

一种特征点检测算法，用于特征提取但不涉及特征描述。SIFT、SURF 的计算量很大，难以满足实时性的要求。Edward Rosten 在 2006 年提出了 FAST 特征检测算法。FAST 算法通过与圆周像素的比较结果判别特征点，计算速度快、可重复性高，非常适合实时视频的处理

FAST 算法逻辑：如果像素点与其周围邻域内多个像素相差较大，则该像素点可能是角点。因此，在以像素点为中心的圆周上均匀地取 16 个像素点，如果其中连续 N 个像素点与中心点的像素值之差都大于设置的阈值，则中心像素被判定为角点。具体有两种情况，一是连续 N 个像素点都比中心点更亮，二是连续 N 个像素点都比中心点更暗，且亮度差都大于设置的阈值 t

img = cv.imread("../images/Circuit04.png", flags=1)  # 基准图像
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)  # (425, 558)
height, width = gray.shape[:2]
print("shape of image: ", height, width)
fast = cv.FastFeatureDetector_create()  # 初始化 FAST 对象
# 默认值：threshold=10, nonmaxSuppression=true, type=FastFeatureDetector::TYPE_9_16
kpNMS1 = fast.detect(img, None)  # 检测关键点
imgFASTnms1 = cv.drawKeypoints(img, kpNMS1, None, color=(255, 0, 0))
# 关闭非极大抑制
fast.setNonmaxSuppression(0)  # nonmaxSuppression=false
kp1 = fast.detect(img, None)
imgFAST1 = cv.drawKeypoints(img, kp1, None, color=(255, 0, 0))
print("\nthreshold: {}".format(fast.getThreshold()))
print("num of Keypoints without NMS: {}".format(len(kp1)))
print("num of Keypoints with NMS: {}".format(len(kpNMS1)))
fastT2 = cv.FastFeatureDetector_create(threshold=20)  # 设置差分阈值为 20
kpNMS2 = fastT2.detect(img, None)  # 检测关键点
imgFASTnms2 = cv.drawKeypoints(img, kpNMS2, None, color=(255, 0, 0))
# 关闭非极大抑制
fastT2.setNonmaxSuppression(0)  # nonmaxSuppression=false
kp2 = fastT2.detect(img, None)
imgFAST2 = cv.drawKeypoints(img, kp2, None, color=(255, 0, 0))
print("\nthreshold: {}".format(fastT2.getThreshold()))
print("num of Keypoints without NMS: {}".format(len(kp2)))
print("num of Keypoints with NMS: {}".format(len(kpNMS2)))
fastT3 = cv.FastFeatureDetector_create(threshold=40)  # 设置差分阈值为 40
kpNMS3 = fastT3.detect(img, None)  # 检测关键点
imgFASTnms3 = cv.drawKeypoints(img, kpNMS3, None, color=(255, 0, 0))
# 关闭非极大抑制
fastT3.setNonmaxSuppression(0)  # nonmaxSuppression=false
kp3 = fastT3.detect(img, None)
imgFAST3 = cv.drawKeypoints(img, kp3, None, color=(255, 0, 0))
print("\nthreshold: {}".format(fastT3.getThreshold()))
print("num of Keypoints without NMS: {}".format(len(kp3)))
print("num of Keypoints with NMS: {}".format(len(kpNMS3)))
show_images([imgFAST1,imgFAST2,imgFAST3])
show_images([imgFAST1,imgFAST2,imgFAST3])

BRIEF 特征点检测算法？

二进制鲁棒独立的特征描述 BRIEF （Binary Robust Independent Elementary Features），对检测到的特征点构造特征描述子，其特点是直接生成二进制字符串作为特征描述符，效率很高
SIFT 使用 128 维的浮点数作为特征描述符，共有 512 个字节；SURF 使用 64/128 维特征描述符，共有 256/512 个字节。由于特征点常常高达数千个，这些特征描述向量所占用的内存很大，而且特征点匹配所需的时间也很长。这些特征描述符往往存在大量的数据冗余，可以进行数据压缩或转换为二进制字符串，以减少内存和加快匹配
BRIEF 描述子提供了一种直接生成二进制字符串的特征描述方法，加快了建立特征描述符的速度，也极大的降低了特征描述符的内存占用和特征匹配的时间。因此，BRIEF 算子是一种对特征点描述符计算和匹配的快速方法

BRIEF 描述子的思想是在关键点 P 的周围以一定模式选取 N 个点对，将 N 个点对的比较结果组合起来作为描述子。为了保持选点的一致性，工程上采用特殊设计的固定模式

img = cv.imread("../images/book01.jpg", flags=1)  # 基准图像
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)  # (425, 558)
height, width = gray.shape[:2]
print("shape of image: ", height, width)
# SIFT 关键点检测 + SIFT 特征描述
# sift = cv.xfeatures2d.SIFT_create()  # OpenCV 早期版本
sift = cv.SIFT.create()  # sift 实例化对象
kpSift = sift.detect(gray, None)  # 关键点检测，kp 为关键点信息（包括方向）
print("shape of keypoints: ", len(kpSift))  # 775
imgSift1 = cv.drawKeypoints(img, kpSift, None)  # 只绘制关键点位置
imgSift2 = cv.drawKeypoints(img, kpSift, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)  # 绘制关键点大小和方向
# SIFT 关键点检测 + BRIEF 特征描述
brief = cv.xfeatures2d.BriefDescriptorExtractor_create()  # BRIEF 特征描述
kpBrief, des = brief.compute(img, kpSift)  # 对 SIFT 检测的关键点，通过 BRIEF 计算描述子
imgBrief1 = cv.drawKeypoints(img, kpBrief, None)
imgBrief2 = cv.drawKeypoints(img, kpBrief, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
# STAR 关键点检测 + BRIEF 特征描述
star = cv.xfeatures2d.StarDetector_create()  # STAR 特征检测
brief2 = cv.xfeatures2d.BriefDescriptorExtractor_create()  # BRIEF 特征描述
kpStar = star.detect(img, None)  # STAR 特征检测
kpBriefStar, des = brief.compute(img, kpStar)  # 通过 BRIEF 计算描述子
imgBriefS1 = cv.drawKeypoints(img, kpBriefStar, None)
imgBriefS2 = cv.drawKeypoints(img, kpBriefStar, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
show_images([imgSift1,imgSift2,imgBrief1])
show_images([imgBrief2,imgBriefS1,imgBriefS2])

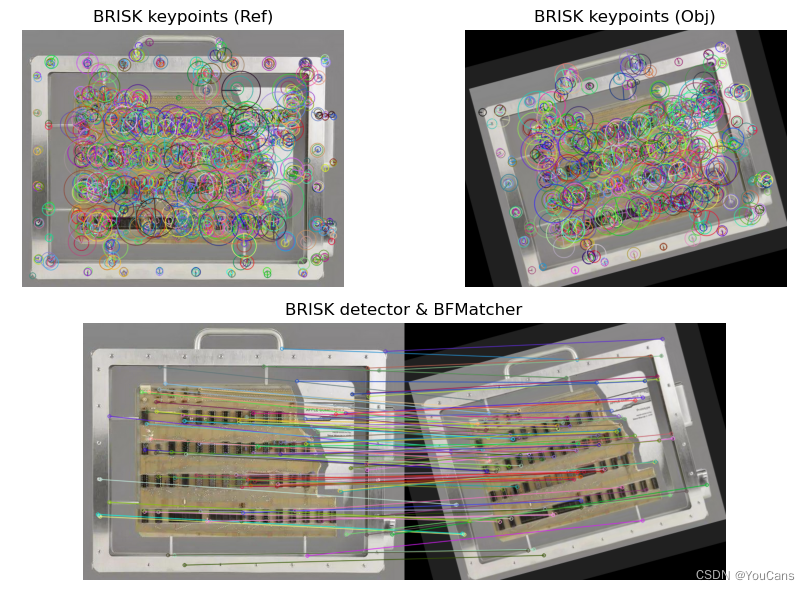
BRISK 特征点检测算法？

尺度不变的二进制特征描述 BRISK （Binary Robust Invariant Scalable Kepoints），是改进的 BRIEF 算法，也是二进制特征描述符。具有高计算效率和旋转不变性、尺度不变性，对噪声也有一定的鲁棒性

imgRef = cv.imread("../images/Circuit04.png", flags=1)  # (480, 600, 3)
refer = cv.cvtColor(imgRef, cv.COLOR_BGR2GRAY)  # 基准图像
height, width = imgRef.shape[:2]  # 图片的高度和宽度
print("shape of image: ", height, width)
# 读取或构造目标图像
top, left = int(0.1*height), int(0.1*width)
border = cv.copyMakeBorder(imgRef, top, top, left, top, borderType=cv.BORDER_CONSTANT, value=(32,32,32))
zoom = cv.resize(border, (width, height), interpolation=cv.INTER_AREA)
theta= 15  # 顺时针旋转角度，单位为角度
x0, y0 = width//2, height//2  # 以图像中心作为旋转中心
MAR = cv.getRotationMatrix2D((x0,y0), theta, 1.0)
imgObj = cv.warpAffine(zoom, MAR, (width, height))  # 旋转变换，默认为黑色填充
# imgObj = cv.imread("../images/Circuit04B.png", flags=1)  # (480, 600, 3)
object = cv.cvtColor(imgObj, cv.COLOR_BGR2GRAY)  # 目标图像
# 构造 BRISK 对象，检测关键点，计算特征描述向量
brisk = cv.BRISK_create()  # 创建 BRISK 检测器
kpRef, desRef = brisk.detectAndCompute(refer, None)  # 基准图像关键点检测
kpObj, desObj = brisk.detectAndCompute(object, None)  # 目标图像关键点检测
imgRefBrisk = cv.drawKeypoints(imgRef, kpRef, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)  # 绘制关键点大小和方向
imgObjBrisk = cv.drawKeypoints(imgObj, kpObj, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)  # 绘制关键点大小和方向
print(desRef.shape, desObj.shape)
# 特征点匹配，Brute-force matcher
matcher = cv.BFMatcher()  # 构造 BFmatcher 对象
matches = matcher.match(desRef, desObj)  # 对描述子 des1, des2 进行匹配
matches = sorted(matches, key=lambda x: x.distance)
matches1 = cv.drawMatches(imgRef, kpRef, imgObj, kpObj, matches[:100], None, flags=2)
show_images([matches1,imgRefBrisk,imgObjBrisk])

ORB 特征点检测算法？

ORB（Oriented FAST and Rotated BRIEF）是一种快速特征点提取和描述的算法，采用改进的 FAST 关键点检测方法，使其具有方向性，并采用具有旋转不变性的 BRIEF 特征描述子。FAST 和 BRIEF 都是非常快速的特征计算方法，因此 ORB 具有非同一般的性能优势。关键过程有两个，一是如何确定关键点；二是如何为关键点生成描述子
FAST 关键点：要想判断一个像素点 p 是不是 FAST 关键点，只需要判断其周围的 16 个像素点中是否有连续 N 个点的灰度值与 p 的差超出阈值

BRIEF 描述子：一种二进制描述子，通常为 128 位的二进制串。它的计算方法是从关键点 p 周围随机挑选 128 个点对，对于每个点对中的两个点，如果前一个点的灰度值大于后一个点，则取 1，反之取 0

img = cv.imread("../images/Fig1701.png", flags=1)
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
print("shape of image: ", gray.shape)
# Initiate ORB detector
orb = cv.ORB_create()  # 实例化 ORB 类
# kp, descriptors = orb.detectAndCompute(gray)  # 检测关键点和生成描述符
kp = orb.detect(img, None)  # 关键点检测，kp 为元组
kp, des = orb.compute(img, kp)  # 生成描述符
print("Num of keypoints: ", len(kp))  # 500
print("Shape of kp descriptors: ", des.shape)  # (500,32)
imgS = cv.convertScaleAbs(img, alpha=0.5, beta=128)
imgKp1 = cv.drawKeypoints(imgS, kp, None)  # 只绘制关键点位置
imgKp2 = cv.drawKeypoints(imgS, kp, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)  # 绘制关键点大小和方向
show_images([img,imgKp1,imgKp2])

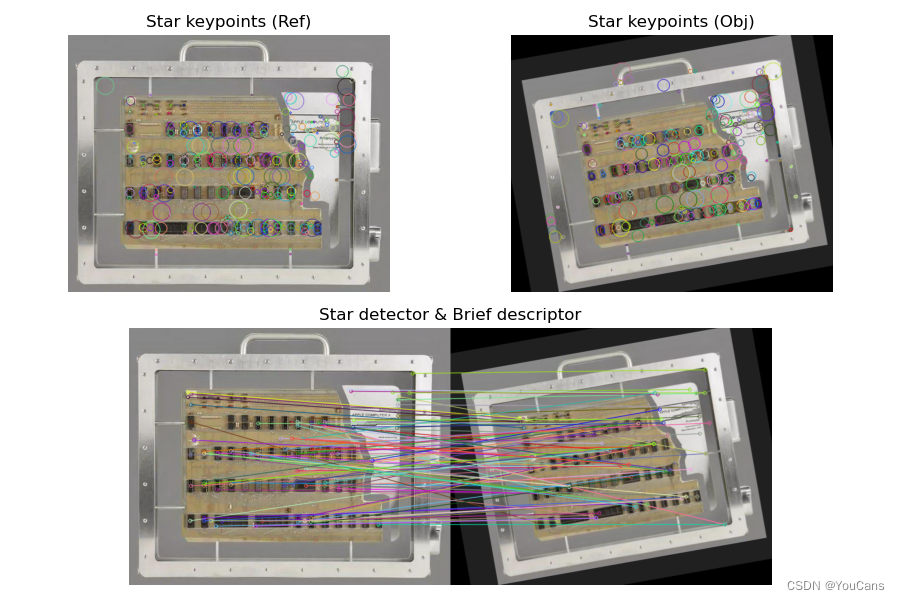
CenSurE 特征点检测算法？

在 CenSurE 算法中，在所有位置和所有尺度计算简化的中心环绕滤波器，并在局部邻域中找到极值

imgRef = cv.imread("../images/Circuit04.png", flags=1)  # (480, 600, 3)
refer = cv.cvtColor(imgRef, cv.COLOR_BGR2GRAY)  # 基准图像
height, width = imgRef.shape[:2]  # 图片的高度和宽度
print("shape of image: ", height, width)  # 480 600
# 读取或构造目标图像
top, left = int(0.1*height), int(0.1*width)
border = cv.copyMakeBorder(imgRef, top, top, left, top, borderType=cv.BORDER_CONSTANT, value=(32,32,32))
zoom = cv.resize(border, (width, height), interpolation=cv.INTER_AREA)
theta= 10  # 顺时针旋转角度，单位为角度
x0, y0 = width//2, height//2  # 以图像中心作为旋转中心
MAR = cv.getRotationMatrix2D((x0,y0), theta, 1.0)
imgObj = cv.warpAffine(zoom, MAR, (width, height))  # 旋转变换，默认为黑色填充
# imgObj = cv.imread("../images/Circuit04B.png", flags=1)  # (480, 600, 3)
object = cv.cvtColor(imgObj, cv.COLOR_BGR2GRAY)  # 目标图像
print("shape of image: ", imgObj.shape)  # (480, 600, 3)
# STAR 关键点检测
star = cv.xfeatures2d.StarDetector_create()  # STAR 特征检测
brief = cv.xfeatures2d.BriefDescriptorExtractor_create()  # BRIEF 特征描述
kpStarRef = star.detect(imgRef, None)  # STAR 基准图像关键点检测
kpStarObj = star.detect(imgObj, None)  # STAR 目标图像关键点检测
# BRIEF 特征描述
kpStarRef, desBriefRef = brief.compute(imgRef, kpStarRef)  # 通过 BRIEF 计算描述子
kpStarObj, desBriefObj = brief.compute(imgObj, kpStarObj)  # 通过 BRIEF 计算描述子
# 特征点匹配，Brute-force matcher
matcher = cv.BFMatcher()  # 构造 BFmatcher 对象
matches = matcher.match(desBriefRef, desBriefObj)  # 对描述子 des1, des2 进行匹配
matches = sorted(matches, key=lambda x: x.distance)
matches1 = cv.drawMatches(imgRef, kpStarRef, imgObj, kpStarObj, matches[:100], None, flags=2)
print('queryIdx=%d' % matches[0].queryIdx)
print('trainIdx=%d' % matches[0].trainIdx)
print('distance=%d' % matches[0].distance)
print("bf.match:{}".format(len(matches)))
imgRefStar = cv.drawKeypoints(imgRef, kpStarRef, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)  # 绘制关键点大小和方向
imgObjStar = cv.drawKeypoints(imgObj, kpStarObj, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)  # 绘制关键点大小和方向
show_images([matches1,imgRefStar,imgObjStar])

特征检测之最大稳定极值区域（MSER）

最大稳定极值区域（MSER-Maximally Stable Extremal Regions），是一种检测图像文本区域的算法，基于分水岭的思想对图像进行斑点区域检测。MSER 算法具有仿射不变性，对灰度的变化具有较强的鲁棒性，但检测准确率低于深度学习方法，主要用于自然场景的文本检测的前期阶段

SER 算法对灰度图像进行阈值处理，阈值从 0 到 255 依次递增，类似于分水岭算法中的水平面的上升。最低点首先被淹没，随着水面的上升逐渐淹没整个山谷，直到所有的点全部被淹没。在不同阈值下，如果某些连通区域不变或变化很小，则该区域称为最大稳定极值区域

def NonMaxSuppression(boxes, thresh=0.5):
	x1, y1 = boxes[:,0], boxes[:,1]
	x2, y2 = boxes[:,0]+boxes[:,2], boxes[:,1]+boxes[:,3]
	area = boxes[:,2] * boxes[:,3]  # 计算面积
	# 删除重复的矩形框
	pick = []
	idxs = np.argsort(y2)  # 返回的是右下角坐标从小到大的索引值
	while len(idxs) > 0:        
		last = len(idxs) - 1  # 将最右下方的框放入pick 数组
		i = idxs[last]
		pick.append(i)
		# 剩下框中最大的坐标(x1Max,y1Max)和最小的坐标(x2Min,y2Min)
		x1Max = np.maximum(x1[i], x1[idxs[:last]])
		y1Max = np.maximum(y1[i], y1[idxs[:last]])
		x2Min = np.minimum(x2[i], x2[idxs[:last]])
		y2Min = np.minimum(y2[i], y2[idxs[:last]])
		# 重叠面积的占比
		w = np.maximum(0, x2Min-x1Max+1)
		h = np.maximum(0, y2Min-y1Max+1)
		overlap = (w * h) / area[idxs[:last]]
		# 根据重叠占比的阈值删除重复的矩形框
		idxs = np.delete(idxs, np.concatenate(([last], np.where(overlap > thresh)[0])))
	return boxes[pick]  # x, y, w, h
img = cv.imread("../images/Fig0944a.tif", flags=1)
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
height, width = gray.shape[:2]
# 创建 MSER 对象，检测 MSER 区域
# mser = cv.MSER_create(_min_area=500, _max_area=20000)
mser = cv.MSER.create(_min_area=306, _max_area=20000)  # 实例化 MSER
regions, boxes = mser.detectRegions(gray)  # 检测并返回找到的 MSER
lenMSER = len(regions)  # 4082
print("Number of detected MSER: ", lenMSER) # 4082
imgMser1 = img.copy()
imgMser2 = img.copy()
for i in range(lenMSER):
	# 绘制 MSER 凸壳
	points = regions[i].reshape(-1, 1, 2)  # (k,2) -> (k,1,2)
	hulls = cv.convexHull(points)
	cv.polylines(imgMser1, [hulls], 1, (255,0,0), 2)  # 绘制凸壳 (x,y)
	#　绘制 MSER 矩形框
	x, y, w, h = boxes[i]  # 区域的垂直矩形边界框
	cv.rectangle(imgMser2, (x,y), (x+w,y+h), (0,0,255), 2)
# 非最大值抑制 (NMS)
imgMser3 = img.copy()
nmsBoxes = NonMaxSuppression(boxes, 0.6)
lenNMS = len(nmsBoxes)  # 149
print("Number of NMS-MSER: ", lenNMS) #149
for i in range(lenNMS):
	#　绘制 NMS-MSER 矩形框
	x, y, w, h = nmsBoxes[i]  # NMS 矩形框
	cv.rectangle(imgMser3, (x,y), (x+w,y+h), (0,255,0), 2)

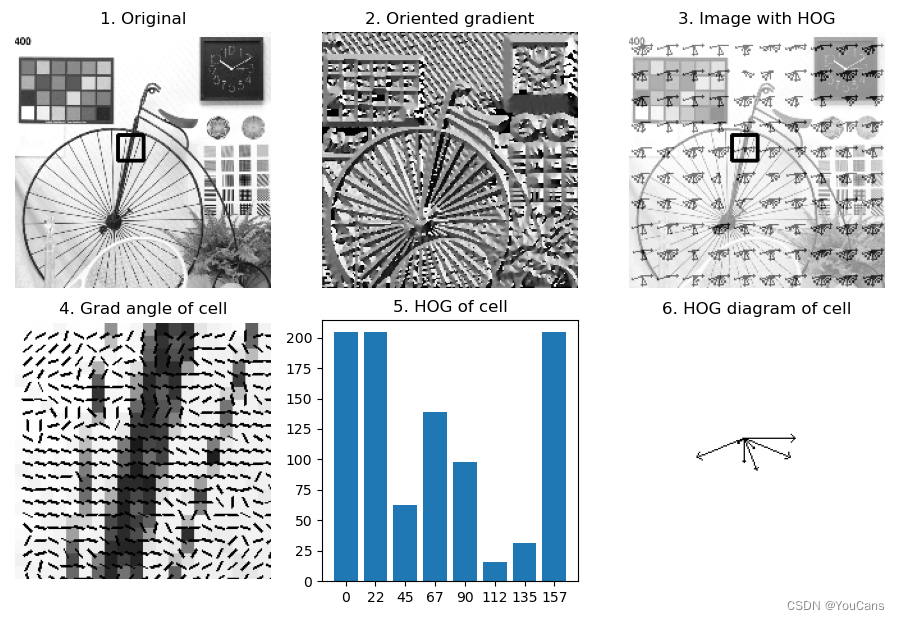
特征描述之 HOG 描述符？

方向梯度直方图（Histogram of Oriented Gradient, HOG）使用梯度方向的分布作为特征来构造描述符，应用非常广泛
梯度的幅值是边缘和角点检测的基础，梯度的方向也包含着丰富的图像特征。HOG 的基本思想，就是图像的局部特征可以用梯度幅值和方向的分布描述。HOG 的基本方法是，将图像划分成多个单元格，计算单元格的方向梯度直方图，把每个单元格的直方图连接起来构造为 HOG 特征向量

HOG 描述符的向量维数不是固定不变的，取决于检测图像大小和单元格的大小。HOG 描述符不具有尺度和旋转不变性，但具有有良好的几何和光学不变性，特别适合人体检测

def drawHOG(image, descriptors, cx, cy, rad):
	angles = np.arange(0, 180, 22.5).astype(np.float32)  # start, stop, step
	normGrad = descriptors/np.max(descriptors).astype(np.float32)
	gx, gy = cv.polarToCart(normGrad*rad, angles, angleInDegrees=True)
	for i in range(angles.shape[0]):
		px, py = int(cx+gx[i]), int(cy+gy[i])
		cv.arrowedLine(image, (cx,cy), (px, py), 0, tipLength=0.1)  # 黑色
	return image
# (1) 读取样本图像，构造样本图像集合
img = cv.imread("../images/Fig1101.png", flags=0)  # 灰度图像
height, width, wCell, d = 200, 200, 20, 10
img = cv.resize(img, (width, height))  # 调整为统一尺寸
# (2) 构造 HOG 检测器
winSize = (20, 20)
blockSize = (20, 20)
blockStride = (20, 20)
cellSize = (20, 20)
nbins = 8
hog = cv.HOGDescriptor(winSize, blockSize, blockStride, cellSize, nbins)
lenHOG = nbins * (blockSize[0]/cellSize[0]) * (blockSize[1]/cellSize[1]) \
		* ((winSize[0]-blockSize[0])/blockStride[0] + 1) \
		* ((winSize[1]-blockSize[1])/blockStride[1] + 1)
print("length of descriptors:", lenHOG)
# (3) 计算检测区域的 HOG 描述符
xt, yt = 80, 80  # 检测区域位置
cell = img[xt:xt+wCell, yt:yt+wCell]
cellDes = hog.compute(cell)  # HOG 描述符，(8,)
normGrad = cellDes/np.max(cellDes).astype(np.float32)
print("shape of descriptors:{}".format(cellDes.shape))
print(cellDes)
# (4) 绘制方向梯度示意图
imgGrad = cv.resize(cell, (wCell*10, wCell*10), interpolation=cv.INTER_AREA)
Gx = cv.Sobel(img, cv.CV_32F, 1, 0, ksize=5)  # X 轴梯度 Gx
Gy = cv.Sobel(img, cv.CV_32F, 0, 1, ksize=5)  # Y 轴梯度 Gy
magG, angG = cv.cartToPolar(Gx, Gy, angleInDegrees=True)  # 极坐标求幅值与方向 (0~360)
print(magG.min(), magG.max(), angG.min(), angG.max())
angCell = angG[xt:xt+wCell, yt:yt+wCell]
box = np.zeros((4, 2), np.int32)  # 计算旋转矩形的顶点, (4, 2)
for i in range(wCell):
	for j in range(wCell):
		cx, cy = i*10+d, j*10+d
		rect = ((cx,cy), (8,1), angCell[i,j])  # 旋转矩形类
		box = np.int32(cv.boxPoints(rect))  # 计算旋转矩形的顶点, (4, 2)
		cv.drawContours(imgGrad, [box], 0, (0,0,0), -1)
# (5) 绘制检测区域的方向梯度直方图
cellHOG = np.ones((201,201), np.uint8)  # 白色
cellHOG = drawHOG(cellHOG, cellDes, xt+d, yt+d, 40)
# (6) 绘制图像的方向梯度直方图
imgHOG = np.ones(img.shape, np.uint8)*255  # 白色
for i in range(10):
	for j in range(10):
		xc, yc = 20*i, 20*j
		cell = img[xc:xc+wCell, yc:yc+wCell]
		descriptors = hog.compute(cell)  # HOG 描述符，(8,)
		imgHOG = drawHOG(imgHOG, descriptors, xc+d, yc+d, 8)
imgWeight = cv.addWeighted(img, 0.5, imgHOG, 0.5, 0)
show_images([img,angNorm,imgWeight,imgGrad,cellHOG])

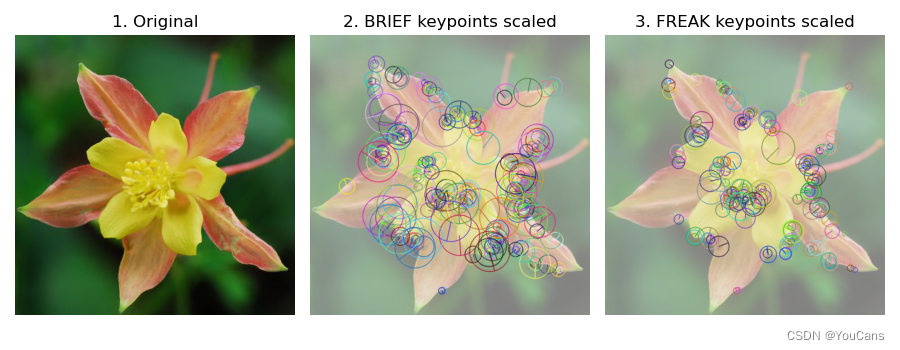
特征检测之视网膜算法（FREAK）？

快速视网膜关键点描述（FREAK，Fast Retina Keypoint）模拟人类视网膜的拓扑结构设计关键点的采样模式，构造二进制编码串珠外关键点的特征描述符，具有速度快、内存占用小和鲁棒性强的优点

BRISK 算法的采样模式是均匀采样模式（在同一圆上等间隔的进行采样），FREAK 算法采取了更为接近于人眼视网膜接收图像信息的采样模型

img = cv.imread("../images/Fig1701.png", flags=1)  # 基准图像
height, width = img.shape[:2]  # (500, 500)
print("shape of image: ({},{})".format(height, width))
# BRISK 检测关键点
brisk = cv.BRISK_create()  # 创建 BRISK 检测器
kp = brisk.detect(img)  # 关键点检测，kp 为元组
print("Num of keypoints: ", len(kp))  # 271
# BRIEF 特征描述
brief = cv.xfeatures2d.BriefDescriptorExtractor_create()  # 实例化 BRIEF 类
kpBrief, desBrief = brief.compute(img, kp)  # 计算 BRIEF 描述符
print("BRIEF descriptors: ", desBrief.shape)  # (270, 32)
# FREAK 特征描述
freak = cv.xfeatures2d.FREAK_create()  # 实例化 FREAK 类
kpFreak, desFreak = freak.compute(img, kp)  # 生成描述符
print("FREAK descriptors: ", desFreak.shape)  # (196, 64)
imgS = cv.convertScaleAbs(img, alpha=0.5, beta=128)
imgKp1 = cv.drawKeypoints(imgS, kpBrief, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
imgKp2 = cv.drawKeypoints(imgS, kpFreak, None, flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
show_images([img,imgKp1,imgKp2])

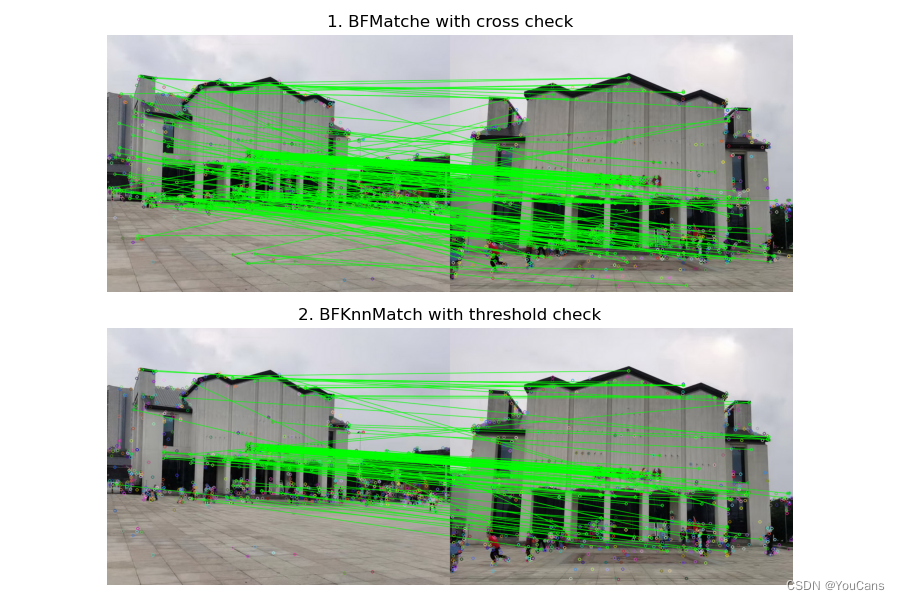
特征匹配之暴力匹配？

基于特征描述符的特征点匹配是通过对两幅图像的特征点集合内的关键点描述符的相似性比对来实现的。分别对参考图像（Reference image）和检测图像（Observation image）建立关键点描述符集合，采用某种距离测度作为关键点描述向量的相似性度量

暴力匹配（Brute-force matcher）是最简单的二维特征点匹配方法。对于从两幅图像中提取的两个特征描述符集合，对第一个集合中的每个描述符 Ri，从第二个集合中找出与其距离最小的描述符 Sj 作为匹配点

imgRef = cv.imread("../images/Fig1703a.png", flags=1)
refer = cv.cvtColor(imgRef, cv.COLOR_BGR2GRAY)  # 参考图像
height, width = imgRef.shape[:2]  # 图片的高度和宽度
# 读取或构造检测图像
imgObj = cv.imread("../images/Fig1703b.png", flags=1)
object = cv.cvtColor(imgObj, cv.COLOR_BGR2GRAY)  # 目标图像
# (2) 构造 SIFT 对象，检测关键点，计算特征描述向量
sift = cv.SIFT.create()  # sift 实例化对象
kpRef, desRef = sift.detectAndCompute(refer, None)  # 参考图像关键点检测
kpObj, desObj = sift.detectAndCompute(object, None)  # 检测图像关键点检测
print("Keypoints: RefImg {}, ObjImg {}".format(len(kpRef), len(kpObj)))  # 2238/1675
# (3) 特征点匹配，暴力匹配+交叉匹配筛选，返回最优匹配结果
bf1 = cv.BFMatcher(crossCheck=True)  # 构造 BFmatcher 对象，设置交叉匹配
matches = bf1.match(desRef, desObj)  # 对描述子 desRef, desObj 进行匹配
# matches = sorted(matches, key=lambda x: x.distance)
imgMatches1 = cv.drawMatches(imgRef, kpRef, imgObj, kpObj, matches[:300], None, matchColor=(0,255,0))
print("(1) bf.match with crossCheck: {}".format(len(matches)))
print(type(matches), type(matches[0]))
print(matches[0].queryIdx, matches[0].trainIdx, matches[0].distance)  # DMatch 的结构和用法
# (4) 特征点匹配，KNN匹配+比较阈值筛选
bf2 = cv.BFMatcher()  # 构造 BFmatcher 对象
matches = bf2.knnMatch(desRef, desObj, k=2)  # KNN匹配，返回最优点和次优点 2个结果
goodMatches = []  # 筛选匹配结果
for m, n in matches:  # matches 是元组
	if m.distance < 0.7 * n.distance:  # 最优点距离/次优点距离 之比小于阈值0.7
		goodMatches.append([m])  # 保留显著性高度匹配结果
# good = [[m] for m, n in matches if m.distance<0.7*n.distance]  # 单行嵌套循环遍历
imgMatches2 = cv.drawMatchesKnn(imgRef, kpRef, imgObj, kpObj, goodMatches, None, matchColor=(0,255,0))
print("(2) bf.knnMatch:{}, goodMatch:{}".format(len(matches), len(goodMatches))) # 1058 1015
print(type(matches), type(matches[0]), type(matches[0][0])) # 363
print(matches[0][0].distance) # 1058 123
show_images([imgMatches1,imgMatches2])

基于拉普拉斯核的图像 “孤立点” 检测？

孤立点的检测，是检测嵌在一幅图像的恒定区域或亮度几乎不变的区域里的孤立点。孤立点的检测以二阶导数为基础

注意：这里孤立点检测，是绝对意义上的孤立点，即一个孤立的像素。人眼所能感知、识别的孤立点，通常来说其实是一个微小的区域，而不是孤立的一个像素，因此并不能用这种方法检测

imgGray = cv2.imread("../images/Fig1004.tif", flags=0)
hImg, wImg = imgGray.shape
# scipy.signal 实现卷积运算 (注意：不能用 cv2.filter2D 处理)
from scipy import signal
kernelLaplace = np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]])  # Laplacian kernel
imgLaplace = signal.convolve2d(imgGray, kernelLaplace, boundary='symm', mode='same')  # same 卷积
# 在原图上用半径为 5 的圆圈标记角点
T = 0.9 * max(imgLaplace.max(), -imgLaplace.min())
imgPoint = np.zeros((hImg, wImg), np.uint8)  # 创建黑色图像
for h in range(hImg):
	for w in range(wImg):
		if (imgLaplace[h, w] > T) or (imgLaplace[h, w] < -T):
			imgPoint[h, w] = 255  # 二值处理
			cv2.circle(imgPoint, (w, h), 10, 255)

参考：