机器学习的过拟合和欠拟合
在搭建机器学习模型时,遇到过拟合、欠拟合的处理办法
什么是误差 (error) ?
- 学习器的实际预测输出与样本的真实输出之间的差异
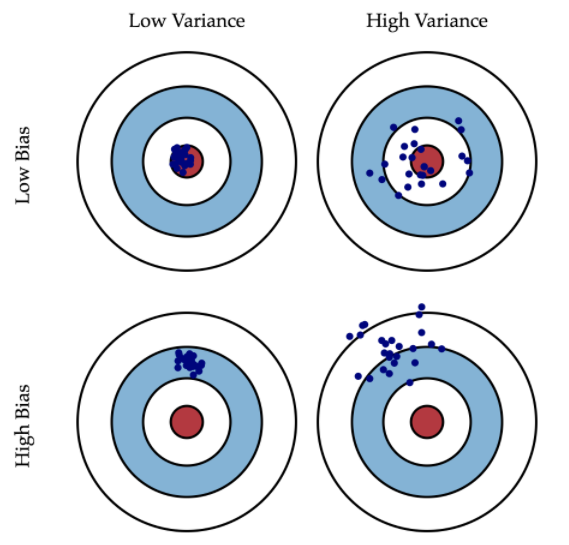
什么是偏差 (Variabce)?
![]()
- 意味着模型训练效果距离理想目标还有很大差距,常常效果很差
什么是方差 (Bias)?
- 意味着模型训练效果时好时坏,虽然有时候效果很好,但不够稳定
什么是泛化误差 (generalization error)?
- 泛化误差 (generalization error) 表示在新样本上的误差,可以分解成偏差 (Variabce) 的平方方差 (Bias) 噪声 (nose)
什么是训练误差 "(training error)?
- ** 训练误差 "(training error) 和经验误差 (empirical error),** 均指学习器在训练集上的误差
什么是模型泛化能力 (generalization)?
- 指的是模型依据训练时采用的数据,针对以前未见过的新数据做出正确预测的能力
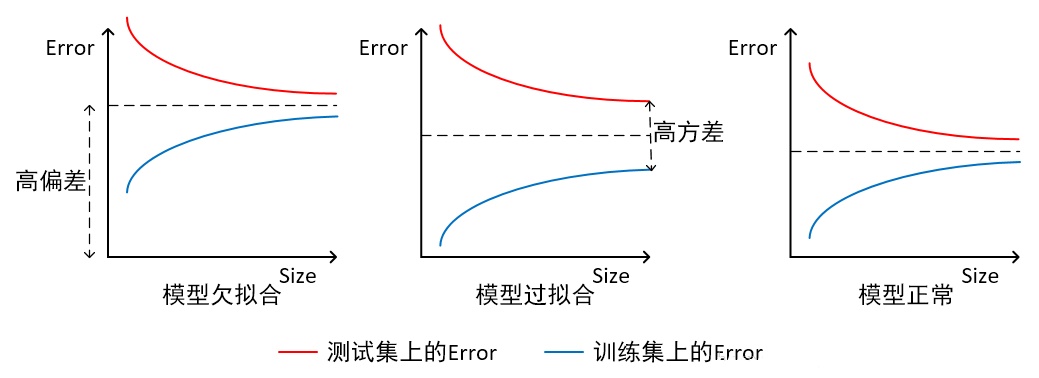
什么是过拟合 (overfitting)?
![]()
- 即模型泛化能力不行,在训练集中得到了方差 (Bias) 和偏差 (Variabce),简单来说就是在训练集上的好效果,不能在测试集上同样获得
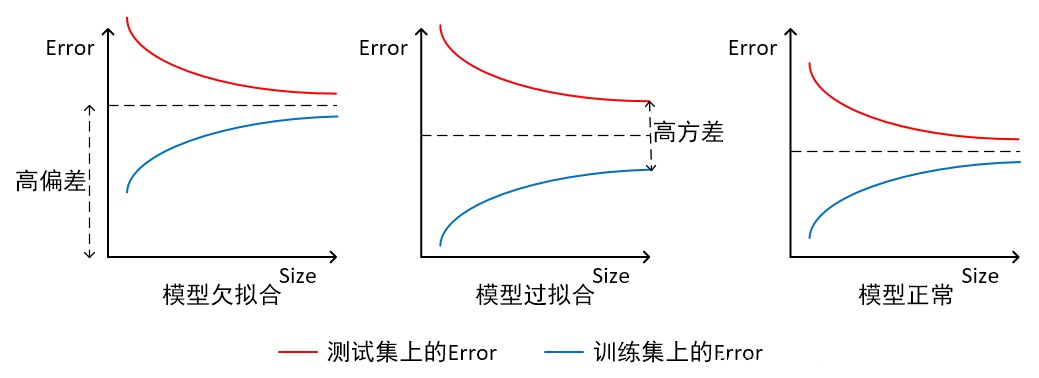
什么是欠拟合 (underfitting)?
![]()
- 指模型拟合程度不高,数据距离拟合曲线较远,或指模型没有很好地捕捉到数据特征,不能够很好地拟合数据
哪些原因导致产生过拟合?
- 数据及模型问题
- 样本选取有误,如样本数量太少,选样方法错误,样本标签错误等,导致选取的样本数据不足以代表预定的分类规则
- 样本噪音干扰过大,使得机器将部分噪音认为是特征从而扰乱了预设的分类规则
- 模型不合理,假设成立的条件实际并不成立
- 参数太多
- 构造过程
- 决策树模型过度生长,其自由生长有可能使节点只包含单纯的事件数据或非事件数据,使其虽然可以完美匹配(拟合)训练数据,但是无法适应其他数据集
- 神经网络迭代次数足够多,拟合了训练数据中的噪声和训练样例中没有代表性的特征
如何解决过拟合 (高方差)?
- 增加训练数据 : 因为过拟合可能原因是数据量太少而模型太复杂,也按照以下方法做数据增广: 在计算机视觉领域中,对图像旋转,缩放,剪切,添加噪声等;在自然语言处理领域中,可以做同义词替换扩充数据集;语音识别中可以对样本数据添加随机的噪声
- 特征选择 : 减少非共线性特征数,降低干扰特征打来的误差,相当与人工选择模型(特征少,模型参数也减少)
- 模型集成 : 装袋算法 (Bagging) 通过平均多个模型的结果,来降低模型的方差提升算法 (Boosting) 不仅能够减小偏差,还能减小方差
- 选择模型参数 : 通过交叉检验得到较优的模型参数
- 降低模型复杂度 : 在数据较少时,适当的降低模型复杂度是比较有效的方法,可以降低模型对噪声的拟合度,有以下方法: 正则项则:可以考虑增大正则项参数,常用的有 L1 正则化 L2 正则化,一般 l2 正则应用比较多;神经网络调参: 减少网络层数,减少神经元个数,dropout,逐层归一化;提前终止;决策树可以控制树的深度,剪枝
如何解决欠拟合 (高偏差)?
- 增加特征(不是增加样本):增加更多的特征,使输入数据具有更强的表达能力,考虑加入进特征组合、高次特征
- 减少正则化参数,减少正则化参数 调整参数和超参数:如神经网络中的学习率、学习衰减率、batch_size 数值、神经网络的隐藏层数和隐藏单元数 ;决策树的深度、随机森林的树数量 K-Means 中的 K 值 使用集成学习 (ensemble) 方法:如 Bagging , 将多个弱学习器 Bagging 选择更加复杂的算法或模型:例如用神经网络来替代,随机森林 (Random Forest) 来代决策树 (ID3,ID4.5,C4.5) 等
算法的误差一般是由那几个方面引起的?
- 数据噪声,表示算法误差下界
- 因模型无法表示基本数据的复杂度而造成的偏差 (bias).— 欠拟合
- 因模型过度拟合训练集数据而造成的方差 (variance).— 过拟合
决策树算法中如何避免过拟合和欠拟合?
- 决策树 (ID3,ID4.5,C4.5) 中,过拟合:剪枝操作 (前置剪枝和后置剪枝);K 折交叉验证
- 欠拟合:增加树的深度随机森林 (Random Forest)
什么是经验风险最小化?
![]()
- 只侧重训练数据集上的损失降到最低;
- 采用了极大似然(MLE)的参数评估方法,更侧重从数据中学习模型的潜在参数,而且是只看重数据样本本身。这样在数据样本缺失的情况下,很容易管中窥豹,模型发生过拟合的状态;
什么是结构风险最小化?
![]()
- 结构风险最小化:在经验风险最小化的基础上约束模型的复杂度,使其在训练数据集的损失降到最低的同时,模型不至于过于复杂,相当于在损失函数上增加正则化 (regularization),防止模型出现过拟合状态。
- 结构风险最小化:采用了最大后验概率估计 (MAP) 的思想来推测模型参数,不仅仅是依赖数据,还依靠模型参数的先验假设。这样在数据样本不是很充分的情况下,我们可以通过模型参数的先验假设,辅助以数据样本,做到尽可能的还原真实模型分布
统计学习中的损失函数、风险函数?
- 用损失函数或代价函数来度量预测错误的程度
- 模型 f (X) 关于联合分布 P (X,Y) 的平均意义下的损失,称为风险函数或期望损失
- 模型 f (X) 关于训练数据集的平均损失称为经验风险或经验损失
- 根大数定律,当样本容量 N 趋于无穷时,经验风险 emp (f) 趋于期望风险 exp (f) 。所以一个很自然的想法是用经验风险估计期望风险