K 近邻 - KNN
直观的分类方法,规定距离内标签最多 K 个样本是当前样本的标签,关键步骤在于确定 K、距离度量和投票方式
什么是形心 (centroid)?
- 聚类的中心,由 K-means 或 k-median 算法决定
- 例如,如果 k 为 3,则 k-means 或 k-median 算法会找出 3 个形心
什么是最近邻 (KNN) 分类?
- 一个对象的类别是由其 k 个最近邻居的 “表决” 确定的,若 k = 1,则该对象的类别直接由最近的一个邻居确定
- K-NN 是一种基于实例的学习,或者是局部近似和将所有计算推迟到分类之后的惰性学习。k - 近邻算法是所有的机器学习算法中最简单的之一
K 近邻三个基本要素?
- k 值的选择
- 距离度量
- 分类决策规则
K 近邻中 K 值的影响及如何选择?
- 选小值,模型变复杂,容易出现过拟合 (overfitting)
- 选大值,模型变简单
- 在应用中, k 值一般取一个比较小的数值。通常采用交叉验证法来选取最优的 k 值
K 近邻的两种 “最近邻搜索策略”?
- 线性扫描:要计算输入实例与每一个训练实例的距离。当训练集很大时,计算非常耗时,这种方法是不可行的
- kd 树搜索:进行局部搜索即可,计算量减少
K 近邻的为什么采用 “多数表决规则” 作为分类规则?
- 采用 “多数表决规则”,多数表决规则等价于经验风险最小化
![]()
K 近邻算法有什么优缺点?
- 优点
- KNN 算法简单、有效
- 对异常值不敏感、无数据输入假定
- 适用数据范围:数值型和标称型
- 由于 KNN 方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN 方法较其他方法更为适合
- 缺点
- KNN 算法计算量较大
- KNN 算法需要事先确定 K 值
- KNN 算法对样本容量较小的类域很容易产生误分
如何构造 K 近邻的 kd 搜索树?
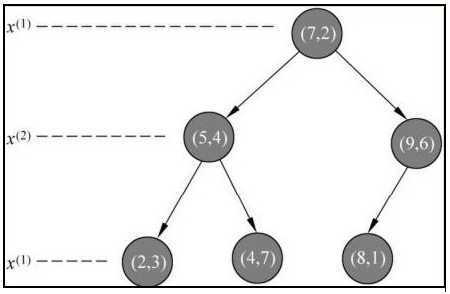
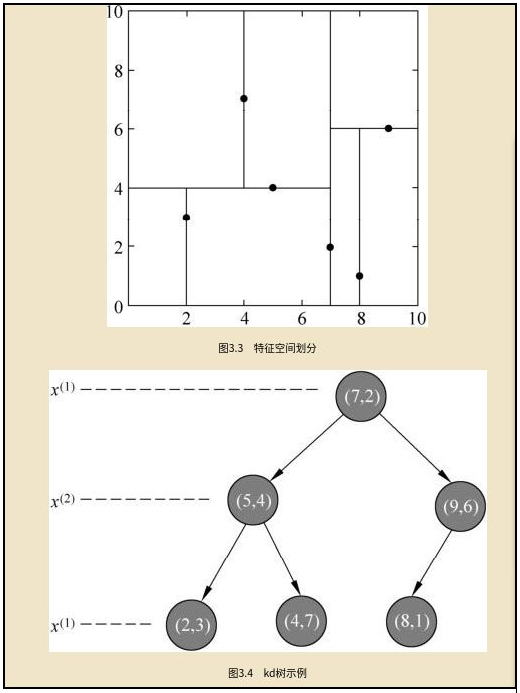
- kd 树是一种对 k 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构, 并且是二叉树
- 构造 kd 树相当于不断地用垂直于坐标轴的超平面将 k 维空间切分(按序循环使用属性划分),构成一系列的 k 维超矩形区域。 kd 树的每个结点对应于一个 k 维超矩形区域
![]()
![]()
解释 K 近邻算法、流程及特点?
- 利用训练数据集对特征向量空间进行划分,并作为其分类的 “模型”;如果一个样本在特征空间中的 k 个最相似(特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别
- 计算距离:计算训练样本和测试样本中每个样本点的距离(常见的距离度量有欧式距离,马氏距离等)
- 排序:对上面所有的距离值进行排序
- 选择样本:选择前 k 个最小距离的样本
- 投票:根据这 k 个样本的标签进行投票,得到最后的分类类别
求二维空间最近邻点?
- 已知二维空间的 3 个点,试求在 p 取不同值时,Lp 距离下 x1 的最近邻点
![]()
构造一个平衡 kd 树?
求 kd 树的最近邻
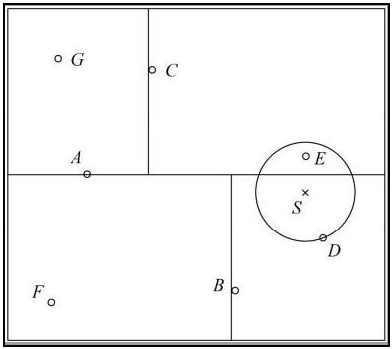
- 给定一个如图 3.5 所示的 kd 树,根结点为 A,其子结点为 B,C 等。树上共存储 7 个实例点;另有一个输入目标实例点 S,求 S 的最近邻
![]()
- 首先在 kd 树中找到包含点 S 的叶结点 D(图中的右下区域),以点 D 作为近似最近邻。真正最近邻一定在以点 S 为中心通过点 D 的圆的内部。然后返回结点 D 的父结点 B,在结点 B 的另一子结点 F 的区域内搜索最近邻。结点 F 的区域与圆不相交,不可能有最近邻点。继续返回上一级父结点 A,在结点 A 的另一子结点 C 的区域内搜索最近邻。结点 C 的区域与圆相交;该区域在圆内的实例点有点 E,点 E 比点 D 更近,成为新的最近邻近似。最后得到点 E 是点 S 的最近邻
scikit-learn 无监督最近邻实现办法?
- NearestNeighbors 实现了无监督的近邻学习。它作为一个统一的接口,连接到三种不同的最近的邻居算法:BallTree、KDTree 和基于 sklearn.metrics.pairwise 中的例程的强制算法。邻居搜索算法的选择是通过关键字 "算法" 控制的,它必须是 [‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’] 中的一个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19>>> from sklearn.neighbors import NearestNeighbors
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> nbrs = NearestNeighbors(n_neighbors=2, algorithm='ball_tree').fit(X)
>>> distances, indices = nbrs.kneighbors(X)
>>> indices
array([[0, 1],
[1, 0],
[2, 1],
[3, 4],
[4, 3],
[5, 4]]...)
>>> distances
array([[0. , 1. ],
[0. , 1. ],
[0. , 1.41421356],
[0. , 1. ],
[0. , 1. ],
[0. , 1.41421356]])
如何理解 scikit-learn 无监督最近邻中的 Ball-tree?
- 用于快速泛化 N 点问题的 BallTree ,最近邻居快速寻找邻居的算法之一
- 为了解决 KD-tree 在更高维度上的低效率问题,我们开发了球树数据结构。KD 树沿直角坐标轴划分数据,而球树则以一系列嵌套的超球体划分数据。这使得树的构造比 KD 树的构造更昂贵,但是这种数据结构在高度结构化的数据上可以非常有效,甚至在非常高的维度上也是如此,查询时间为:
1
2
3
4
5
6
7
8
9
10>>> import numpy as np
>>> from sklearn.neighbors import BallTree
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((10, 3)) # 10 points in 3 dimensions
>>> tree = BallTree(X, leaf_size=2)
>>> dist, ind = tree.query(X[:1], k=3)
>>> print(ind) # indices of 3 closest neighbors
[0 3 1]
>>> print(dist) # distances to 3 closest neighbors
[ 0. 0.19662693 0.29473397]
如何理解 scikit-learn 无监督最近邻中的 KD-tree?
- 用于快速泛化 N 点问题的 KDTree,最近邻居快速寻找邻居的算法之一
- 通过有效编码样本的总距离信息来减少所需的距离计算次数。其基本思想是,如果 A 点与 B 点非常遥远,而 B 点与 C 点非常接近,那么我们就知道 A 点和 C 点非常遥远,而不必明确计算它们的距离。
- 对于小的 D(小于 20 个左右),查询成本大约是 O [Dlog (N)],KD 树查询可以非常有效。对于较大的 D,查询成本增加到近 O [DN],并且由于树状结构的开销会导致查询比蛮力更慢
1
2
3
4
5
6
7
8
9
10>>> import numpy as np
>>> from sklearn.neighbors import KDTree
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((10, 3)) # 10 points in 3 dimensions
>>> tree = KDTree(X, leaf_size=2)
>>> dist, ind = tree.query(X[:1], k=3)
>>> print(ind) # indices of 3 closest neighbors
[0 3 1]
>>> print(dist) # distances to 3 closest neighbors
[ 0. 0.19662693 0.29473397]
scikit-learn 中最近邻算法如何进行分类任务?
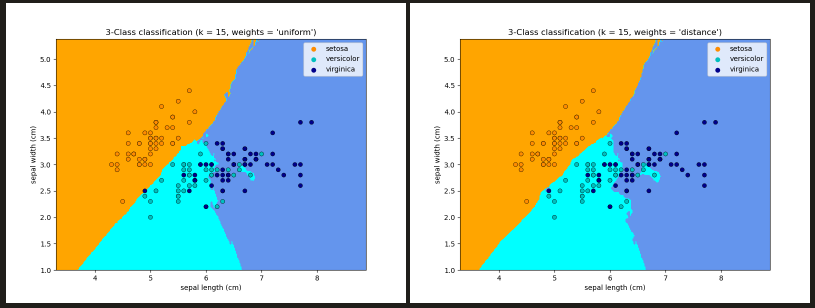
- 基于邻居的分类是一种基于实例的学习或非泛化学习:它不试图构建一个通用的内部模型,而是简单地存储训练数据的实例。分类是通过每个点的近邻的简单多数投票来计算的:一个查询点被分配到在该点的近邻中拥有最多代表的数据类别
- scikit-learn 实现了两种不同的近邻分类器,KNeighborsClassifier 基于每个查询点的 k 个最近的邻居的学习,其中 k 是用户指定的整数值;**RadiusNeighborsClassifier:** 基于每个训练点的固定半径 r 内的邻居数量进行学习,其中 r 是用户指定的浮点值
- 基本的近邻分类使用统一的权重:也就是说,分配给一个查询点的值是由近邻的简单多数投票计算出来的,即 weights = ‘uniform’ ; weights = ‘distance’,按与查询点距离的倒数分配权重。或者,可以提供一个用户定义的距离函数来计算权重
![]()
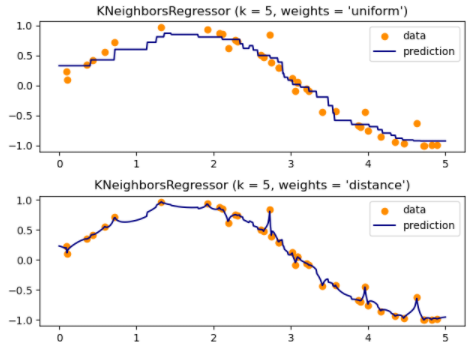
最近邻算法如何进行回归任务?
- 基于邻居的回归可用于数据标签为连续变量而非离散变量的情况。分配给查询点的标签是根据其最近的邻居的标签的平均值计算出来的
- scikit-learn 实现了两种不同的邻居回归器。**KNeighborsRegressor:** 基于每个查询点的 k 个最近的邻居的学习,其中 k 是用户指定的整数值。**RadiusNeighborsRegressor:** 基于查询点的固定半径 r 内的邻居的学习,其中 r 是用户指定的浮点值
- 基本的近邻分类使用统一的权重:也就是说,分配给一个查询点的值是由近邻的简单多数投票计算出来的,即 weights = ‘uniform’ ; weights = ‘distance’,按与查询点距离的倒数分配权重。或者,可以提供一个用户定义的距离函数来计算权重
![]()
scikit-learn 中最近邻算法如何实现快速搜索最近邻?
- brute force (暴力实现): 最天真的邻居搜索实现方式包括对数据集中所有点对之间的距离进行粗暴的计算:对于 D 维中的 N 个样本,构建规模为 ,查询规模为
- KD-tree
- Ball-tree
如何理解 scikit-learn 最近质心分类?
- NearestCentroid 分类器是一种简单的算法,它通过其成员的中心点来代表每个类别。实际上,这使它类似于 KMeans 算法的标签更新阶段。它也没有参数需要选择,这使它成为一个很好的基准分类器
1
2
3
4
5
6
7
8
9>>> from sklearn.neighbors import NearestCentroid
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = NearestCentroid()
>>> clf.fit(X, y)
NearestCentroid()
>>> print(clf.predict([[-0.8, -1]]))
[1]
如何理解 scikit-learn 最近邻转换器?
- 许多 scikit-learn 估计器都依赖于最近的邻居。一些分类器和回归器,如 KNeighborsClassifier 和 KNeighborsRegressor,还有一些聚类方法,如 DBSCAN 和 SpectralClustering,以及一些流形嵌入,如 TSNE 和 Isomap
1
2
3
4
5
6
7
8
9
10
11
12
13
14>>> import tempfile
>>> from sklearn.manifold import Isomap
>>> from sklearn.neighbors import KNeighborsTransformer
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.datasets import make_regression
>>> cache_path = tempfile.gettempdir() # we use a temporary folder here
>>> X, _ = make_regression(n_samples=50, n_features=25, random_state=0)
>>> estimator = make_pipeline(
... KNeighborsTransformer(mode='distance'),
... Isomap(n_components=3, metric='precomputed'),
... memory=cache_path)
>>> X_embedded = estimator.fit_transform(X)
>>> X_embedded.shape
(50, 3)
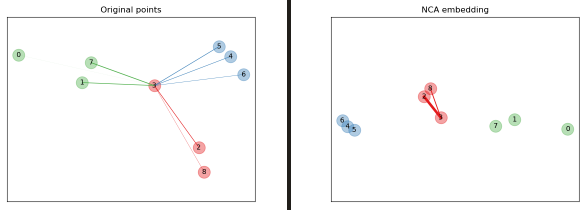
什么是邻里成分分析(NCA,NeighborhoodComponentsAnalysis)?
- 邻里成分分析(NCA,NeighborhoodComponentsAnalysis)是一种距离度量学习算法,与标准的欧氏距离 (L2 距离) 相比,旨在提高近邻分类的准确性。该算法直接将训练集上的随机变体留出的 k - 近邻(KNN)得分最大化。它还可以学习数据的低维线性投影,可用于数据的可视化和快速分类
![]()
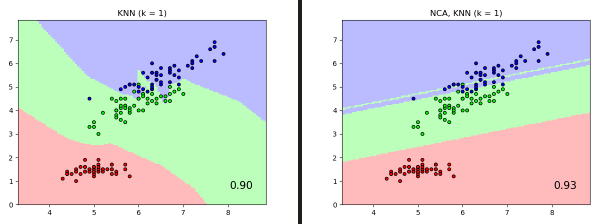
邻里成分分析(NCA,NeighborhoodComponentsAnalysis)如何应用到分类任务?
- NeighborhoodComponentsAnalysis 实例与一个在投影空间中执行分类的 KNeighborsClassifier 实例结合起来
![]()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15>>> from sklearn.neighbors import (NeighborhoodComponentsAnalysis,
... KNeighborsClassifier)
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import Pipeline
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... stratify=y, test_size=0.7, random_state=42)
>>> nca = NeighborhoodComponentsAnalysis(random_state=42)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> nca_pipe = Pipeline([('nca', nca), ('knn', knn)])
>>> nca_pipe.fit(X_train, y_train)
Pipeline(...)
>>> print(nca_pipe.score(X_test, y_test))
0.96190476...
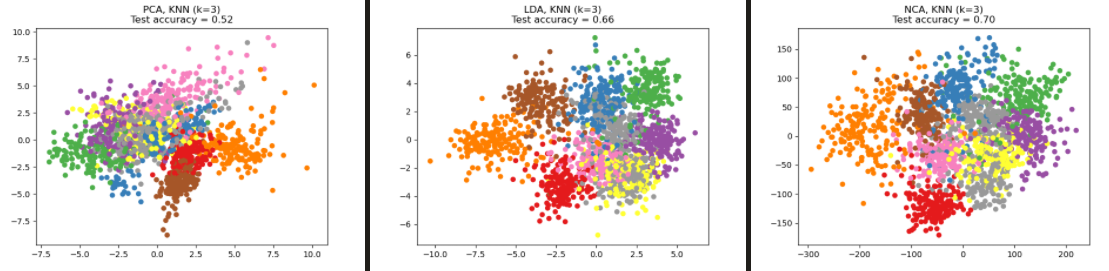
邻里成分分析(NCA,NeighborhoodComponentsAnalysis)如何应用到降维任务?
- NCA 可以用来进行有监督的降维。输入的数据被投射到一个由最小化 NCA 目标的方向组成的线性子空间。所需的维度可以通过参数 n_components 来设置
![]()