VQ-VAE
(图 A->z)->z’ (离散化)-> 图 A’,随机图片
什么是 VQ-VAE ?
![]()
- 在 VAE 上,中间隐变量 z 被约束服从正态分布,后续在正态分布上采样,输入解码器可以生成有意义的图片,但是隐变量 z 的每一维是连续值,这和自然界期待生成样本的方式不符合,比如一般来说,我希望生成 “狗” 的样本,但是不知道从正态分布如何采样才能生成
- VQ-VAE 在隐变量前插入 “codebook”(DxK),将提取的特征 (DxHxW),从 K 个 D 维特征拿出最近的 HxW 个,作为表示当前图片的特征
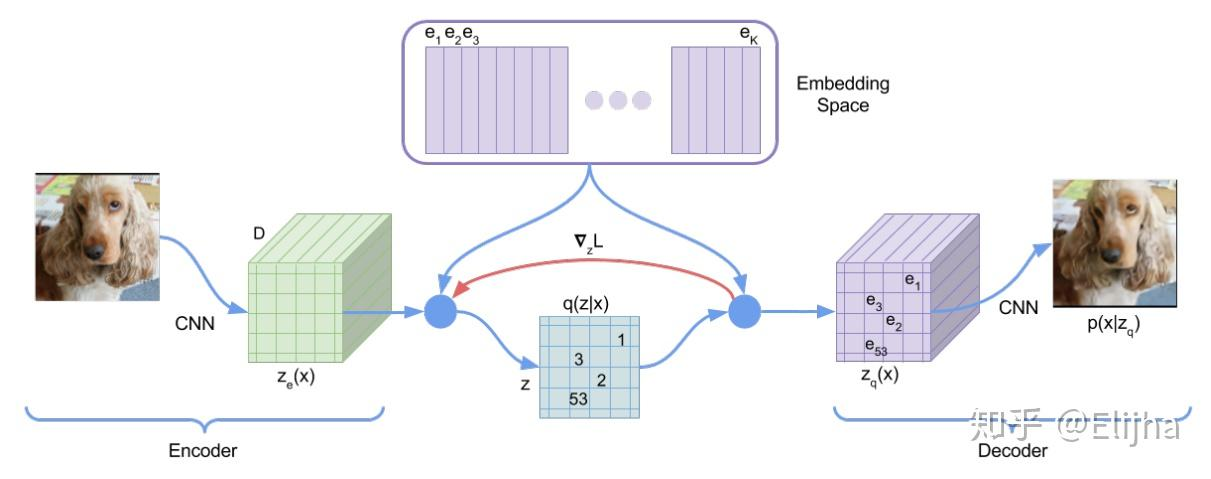
VQ-VAE 的网络结构?
![]()
- 编码器:从图片提取特征,得到特征 (DxH’xW’)
- 查询 codebook: 根据提取到的特征,查询 codebook (DxN) 与之最近的隐变量索引,得到离散化后的特征 (1xH’xW’)
- 解码器:离散化后的特征通过 one-hot,得到 (NxH’xW’),输入解码器后,输出 (1xHxW)
如何理解 VQ-VAE 的 “codebook” 过程?
- 查询 “codebook” 过程就是输入特征 (HW, D),根据 codebook (N, D) 查询之最近的隐变量索引,得到最近索引表 (HW, 1),然后从 codebook 取出对应索引的过程。假设 N=512,D=64,HW=128,那么就是从 512 个 64 维向量中取出 128 个,代表当前图片特征
- 1)隐变量 q (z|x) 的取值范围为整数索引,相应隐空间为所有索引构成的空间,因此是离散的
- 2)codebook 里的 codes 是可学习的,随着训练过程自适应地调整
- 3)从 到 这个变化可以看成一个聚类,即把 encoder 得到的乱七八糟的向量用 codebook 里离它最近的一个 embedding 代表;也可以看成一个特殊的 non-linear transformation
VQ-VAE 的损失函数?
- 在 VQ-VAE 中,codebook 里的 codes 是可学习的,随着训练过程自适应地调整。所以可学习的参数一共包含编码器、解码器和 codebook 三个部分。如果我们简单地取先验分布 p (z) 为离散的均匀类别分布,那么一件有趣的事情是 ELBO 中 KL 正则项变成了常
- 于是 ELBO 只剩下了重构项 . 然而重构项并不能训练到 codebook,所以最终的损失函数其实是这样
- reconstruction 重构误差 :可以看到这里重构误差与普通的 AutoEncoder 重构误差不一样,因为使用了量子化,解码器的输入变为量子化后的字典向量 e。这一项同时更新编码器和解码器
- vq 训练 codebook:编码器得到的潜在向量与字典向量的距离,并将其作为辅助误差项。此误差项只向字典向量 e 传递,通过对误差惩罚来学习 e 向量,不更新编码器和解码器。目的是让 codebook 里的 codes 接近编码器的输出
- commitment 训练编码器 :计算潜在向量与字典向量的距离。不过这里对字典向量 e 使用了 stop gradient 约束,使得此误差项只向编码器反向传递。目的是让编码器的输出接近对应的 codes,避免输出波动太大在 codes 之间乱跳,影响训练
- sg 是 stop gradient 的缩写,表示不对 sg [] 方括号里的变量计算梯度,误差不向此变量传递,在 bp 的时候 的梯度直接 copy 给 ,在 pytorch 中可以用
detach()操作实现
VQ-VAE 如何生成图像?
- 设输入图像 ,其编码器输出为 ,量化操作的索引矩阵记作 ,VQ-VAE 并没有对索引矩阵中索引之间的关系进行建模,如果我们直接随机均匀采样 个索引凑在一起组成一张索引矩阵,它大概率并不对应一个自然图像的编码结果,所以也不能生成一个自然图像
- 因此,为了生成新图像,我们必须学习一个新的生成模型,对索引之间的分布做建模。鉴于索引是离散的,一个自然的选择就是 PixelCNN. 如果是音频数据,那么就用 WaveNet. 当然,也可以利用比较火的 transformer
VQ-VAE 的 Index Collapse & Perplexity 问题?
- Index Collapse & Perplexity 问题:编码器输出的所有特征向量全部被量化到一个或少数几个 codes 上
- 在代码实现中有一个 trick 是输出 perplexity 来监视是否发生了 index collapse. 当发生 index collapse 时,所有特征向量被量化到一个或少数几个 codes 上,这意味着熵很低;而理想情况是各个索引被均匀地选到,意味着熵很高
- 因此,perplexity 可以视作平均有多少个索引会被选择。如果训练时发现 perplexity 太小,甚至是 1,那就要赶紧处理 index collapse 问题了
AE 、 VAE、VQ-VAE 的关系?
- AE:包括编码器和解码器,编码器任务是将图片变化到隐变量 z、解码器任务是从隐变量还原图片
- VAE:在 VAE 中,encoder 不再直接输出 隐向量 z,而是输出隐向量 z 的分布的均值 μ 与标准差 σ,再从这个分布中采样得到隐向量 z
- VQ-VAE:VAE 想学到连续 (continuous) 的隐空间,而 VQ-VAE 想学到离散 (discrete) 的隐空间。VQ-VAE 的 隐空间 codebook 中的 隐向量 是离散的,数量是固定有点多个的;而 VAE 的 隐空间 中的 隐向量 是连续的,数量是无限多个的
参考: