机器学习模型计算模型在数据集上的效果,包括分类、聚类、回归等平均函数
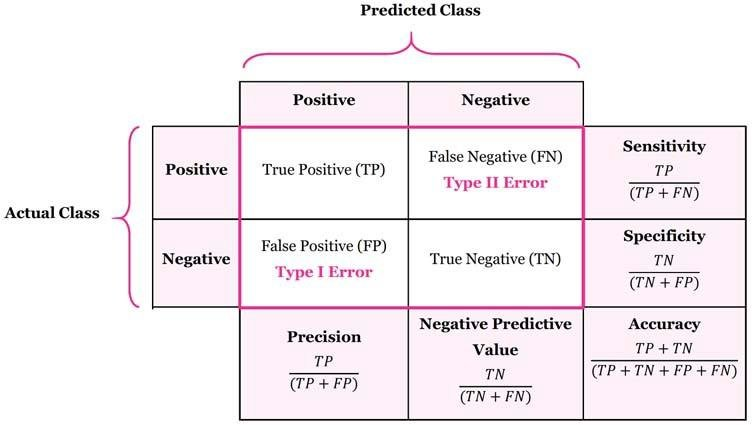
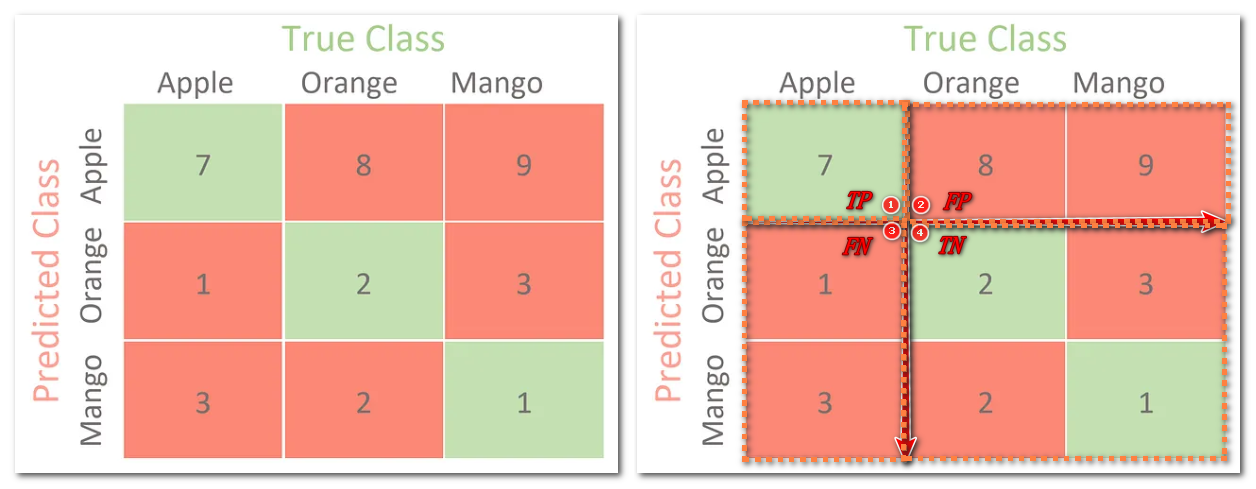
对于分类任务,术语真阳性 (TP)、真阴性 (TN)、假阳性 (FP) 和假阴性 (FN),术语 “阳” 和 “阴” 指的是分类器的预测,术语 “真” 和 “假” 指的则是该预测是否符合外部判断 Positive (P) :正样本Negative (N) :负样本TP :预测为正样本,实际为正样本FP :预测为正样本,实际为负样本FN :预测为负样本,实际为正样本TN :预测为负样本,实际为负样本混淆矩阵是用来总结一个分类器结果的矩阵。对于二分类来说,其混淆矩阵是 2 x 2,对于多分类来说,其混淆矩阵是 kx k 统计 TP、FP、TN、FN:对于二分类来说,其混淆矩阵四个值就是这四个值;对于多分类来说,因为没有所谓的正样本,所以需要拆分每个类去统计这 4 个值,下图统计 Apple 类的 4 个值分别为 {7,8+9,2+3+2+1,1+3}: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 >>> y_true = [0 , 0 , 0 , 1 , 1 , 1 , 1 , 1 ]>>> y_pred = [0 , 1 , 0 , 1 , 0 , 1 , 0 , 1 ]>>> confusion_matrix(y_true, y_pred, normalize='all' ) array([[0.25 , 0.125 ], [0.25 , 0.375 ]]) >>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() >>> tn, fp, fn, tp (2 , 1 , 2 , 3 ) >>> y_true = ["cat" , "ant" , "cat" , "cat" , "ant" , "bird" ]>>> y_pred = ["ant" , "ant" , "cat" , "cat" , "ant" , "cat" ]>>> confusion_matrix(y_true, y_pred, labels=["ant" , "bird" , "cat" ]) array([[2 , 0 , 0 ], [0 , 0 , 1 ], [1 , 0 , 2 ]])
a c c u r a c y ( y , y ′ ) = 1 n ∑ 1 n 1 ( y = y ′ ) = T P + T N T P + F P + T N + F N accuracy(y,y')=\frac{1}{n}\sum_1^{n}1(y=y')=\frac{TP+TN}{TP+FP+TN+FN} a c c u r a c y ( y , y ′ ) = n 1 1 ∑ n 1 ( y = y ′ ) = T P + F P + T N + F N T P + T N
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 >>> import numpy as np >>> from sklearn.metrics import accuracy_score >> X=np.array([0 ,2 ,1 ,3 ]) >> Y=np.array([0 ,1 ,2 ,3 ]) >>> X==Y array([ True , False , False , True ]) >>> np.sum (X==Y) 2 >>> np.sum (X==Y)/len (X) 0.5 >>> accuracy_score(y_true,y_pred,normalize=False ) 2 >>> accuracy_score(y_true,y_pred) 0.5 // 多标签情况下,需要绝对匹配才算预测准确 >>> accuracy_score(np.array([[0 ,1 ],[1 ,1 ]]),np.ones((2 ,2 ))) 0.5
该值是准确率 (accuracy) 的泛化,不同之处在于,只要真实标签被最高分数的前 K 个命中即认为是正确的。K=1 时,该指标等于正确率 a c c u r a c y ( y , y ′ ) = 1 n ∑ i = 1 n ∑ j = 1 k 1 ( y i = y j ′ ) accuracy(y,y')=\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^k1(y_i=y_j') a c c u r a c y ( y , y ′ ) = n 1 i = 1 ∑ n j = 1 ∑ k 1 ( y i = y j ′ )
1 2 3 4 5 6 7 8 9 10 11 12 >>> import numpy as np >>> from sklearn.metrics import top_k_accuracy_score >>> y_true = np.array([0 , 1 , 2 , 2 ]) >>> y_score = np.array([[0.5 , 0.2 , 0.2 ], ... [0.3 , 0.4 , 0.2 ],... [0.2 , 0.4 , 0.3 ],... [0.7 , 0.2 , 0.1 ]]) >>> top_k_accuracy_score(y_true, y_score, k=2 ) 0.75 >>> >>> top_k_accuracy_score(y_true, y_score, k=2 , normalize=False ) 3
该指标用于解决不平衡数据下 直接使用准确率导致的性能偏高的问题,对于平衡数据集,该指标等于准确率 (accuracy),它是每个类 的召回率和真阴性率的平 b a l a n c e d A c c u r a c y = T P V + N P V 2 = T P / ( T P + F N ) + T N / ( T N + F P ) 2 balancedAccuracy=\frac{TPV+NPV}{2}=\frac{TP/(TP+FN)+TN/(TN+FP)}{2} b a l a n c e d A c c u r a c y = 2 T P V + N P V = 2 T P / ( T P + F N ) + T N / ( T N + F P )
1 2 3 4 5 6 >>> from sklearn.metrics import balanced_accuracy_score >>> y_true = [0 , 1 , 0 , 0 , 1 , 0 ] >>> y_pred = [0 , 1 , 0 , 0 , 0 , 1 ] >>> balanced_accuracy_score(y_true, y_pred) 0.625
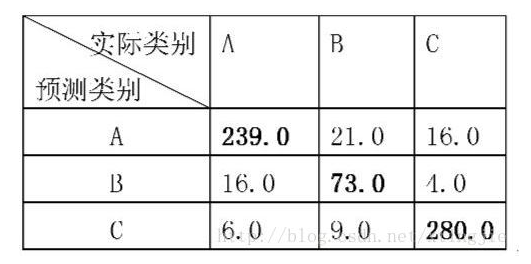
kappa 系数用来 衡量两种标注结果的吻合程度 ,用于评价分类模型,标注指的是把 N 个样本标注为 C 个互斥类别 k a p p a = p o − p e 1 − p e kappa = \frac{p_o-p_e}{1-p_e} k a p p a = 1 − p e p o − p e
现有例子, p 0 = 239 + 73 + 289 664 − 0.8916. p e = 263 × 296 + 103 + 33 + 360 × 205 664 × 604 = 0.3884 k = 0.8916 − 0.3883 1 − 0.3883 . \begin{aligned}p_0=\frac{239+73+289}{664}-0.8916.\\ p_e=\frac{263\times296+103+33+360\times205}{664\times604}=0.3884\\ k=\frac{0.8916-0.3883}{1-0.3883}.\end{aligned} p 0 = 6 6 4 2 3 9 + 7 3 + 2 8 9 − 0 . 8 9 1 6 . p e = 6 6 4 × 6 0 4 2 6 3 × 2 9 6 + 1 0 3 + 3 3 + 3 6 0 × 2 0 5 = 0 . 3 8 8 4 k = 1 − 0 . 3 8 8 3 0 . 8 9 1 6 − 0 . 3 8 8 3 .
kappa 分数是介于 -1 和 1 之间的数字。高于 0.8 的分数通常被认为是良好的一致性;零或更低意味着没有协议(实际上是随机标签) 可以为二元或多类问题计算 Kappa 分数,但不能针对多标签问题 1 2 3 4 5 >>> from sklearn.metrics import cohen_kappa_score >>> y_true = [2 , 0 , 2 , 2 , 0 , 1 ] >>> y_pred = [0 , 0 , 2 , 2 , 0 , 2 ] >>> cohen_kappa_score(y_true, y_pred) 0.4285714285714286
1 2 3 4 5 6 7 8 9 10 11 12 >>> from sklearn.metrics import classification_report >>> y_true = [0 , 1 , 2 , 2 , 0 ] >>> y_pred = [0 , 0 , 2 , 1 , 0 ] >>> target_names = ['class 0' , 'class 1' , 'class 2' ] >>> print (classification_report(y_true, y_pred, target_names=target_names)) precision recall f1-score support class 0 0.67 1.00 0.80 2 class 1 0.00 0.00 0.00 1 class 2 1.00 0.50 0.67 2 accuracy 0.60 5 macro avg 0.56 0.50 0.49 5 weighted avg 0.67 0.60 0.59 5
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数,换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数 L Hamming ( y , y ^ ) = 1 n labels ∑ j = 0 n l a b e l s − 1 1 ( y ^ j ≠ y j ) L_{\text {Hamming }}(y, \hat{y})=\frac{1}{n_{\text {labels}}} \sum_{j=0}^{n_{labels}-1} 1\left(\hat{y}_{j} \neq y_{j}\right) L Hamming ( y , y ^ ) = n labels 1 j = 0 ∑ n l a b e l s − 1 1 ( y ^ j = y j )
1 2 3 4 5 6 7 >>> from sklearn.metrics import hamming_loss >>> y_pred = [1 , 2 , 3 , 4 ] >>> y_true = [2 , 2 , 3 , 4 ] >>> hamming_loss(y_true, y_pred) 0.25 >>> hamming_loss(np.array([[0 , 1 ], [1 , 1 ]]), np.zeros((2 , 2 ))) 0.75
又称查全率、真阳性率 (true positive rate, TPR)、灵敏度 (sensitivity),定义为正确预测的正例数 / 实际正例总数 R e c a l l = T P / ( 真实 P 总数 ) = T P / ( T P + F N ) Recall =TP/(真实 P 总数) =TP/(TP+FN) R e c a l l = T P / ( 真 实 P 总 数 ) = T P / ( T P + F N )
1 2 3 4 5 6 7 8 9 10 11 >>> from sklearn.metrics import recall_score >>> y_true = [0 , 1 , 2 , 2 , 1 , 0 ] >>> y_pred = [0 , 2 , 1 , 0 , 1 , 0 ] >>> recall_score(y_true, y_pred, average='macro' ) 0.5 >>> recall_score(y_true, y_pred, average='micro' ) 0.5 >>> recall_score(y_true, y_pred, average='weighted' ) 0.5 >>> recall_score(y_true, y_pred, average=None ) array([1. , 0.5 , 0. ])
又称查准率、阳性预测值 (positive predictive value, PPV),表示为正确预测的正例数 / 预测正例总数, P r e c i s i o n = T P / ( 预测 P 总数 ) = T P / ( T P + F P ) Precision =TP/(预测 P 总数) =TP/(TP+FP) P r e c i s i o n = T P / ( 预 测 P 总 数 ) = T P / ( T P + F P )
1 2 3 4 5 6 7 8 9 10 11 12 from sklearn.metrics import precision_score >>> y_true = [0 , 1 , 2 , 2 , 1 , 0 ] >>> y_pred = [0 , 2 , 1 , 0 , 1 , 0 ] >>> precision_score(y_true, y_pred, average='macro' ) 0.38888888888888884 >>> precision_score(y_true, y_pred, average='micro' ) 0.5 >>> precision_score(y_true, y_pred, average='weighted' ) 0.38888888888888884 >>> precision_score(y_true, y_pred, average=None ) array([0.66666667 , 0.5 , 0. ])
F P R = F P N = F P F P + T N FPR=\frac{FP}{N}=\frac{FP}{FP+TN} F P R = N F P = F P + T N F P
F 值是精确率 (Precision) 和召回率 (Recall) 评估指标的调和值,假设召回率的权重是精准率的 β 倍,F 值通式为 F − S c o r e = ( 1 + β 2 ) ∗ P r e c i s i o n ∗ R e c a l l ( β 2 ∗ P r e c i s i o n ) + R e c a l l F-Score=(1+\beta^2)*\frac {Precision*Recall} {(\beta^2*Precision)+Recall} F − S c o r e = ( 1 + β 2 ) ∗ ( β 2 ∗ P r e c i s i o n ) + R e c a l l P r e c i s i o n ∗ R e c a l l
根据 β 的不同,F 值倾向不同,β<1 时,侧重精准率(查准率);β>1 时,侧重召回率(查全率);β=1 时,两者重要性相同。一般来说,使用 β=1 较多,即 F1 分数值,用于评价二分类模型 宏标准(Macro-F1) :先统计各个类别的 TP、FP、FN、TN,然后分别计算各自的 Precision 和 Recall,并得到各自的 F1 值,最后取平均值。宏标准(macro)平等地看待各个类别,它的值会受到稀有类别的影响;而微标准(Micro)则更容易受到常见类别的影F 1 s c o r e i = 2 ∗ R e c a l l i ∗ P r e c i s i o n i R e c a l l i + P r e c i s i o n i m a c r o − F 1 s c o r e = ∑ i = 1 N F 1 s c o r e i N F1score_i=2*\frac{Recall_i*Precision_i}{Recall_i+Precision_i}\\ macro-F1score=\frac{\sum_{i=1}^NF1score_i}{N} F 1 s c o r e i = 2 ∗ R e c a l l i + P r e c i s i o n i R e c a l l i ∗ P r e c i s i o n i m a c r o − F 1 s c o r e = N ∑ i = 1 N F 1 s c o r e i
Micro-F1 (微标准) :先统计各个类别的 TP、FP、FN、TN,然后计算总的 Precision 和 Recall,并得到总的 F1 值,也即 Micro-F1。 若数据极度不平衡会影响结R e c a l l a l l = T P 1 + T P 2 + T P 3 + … T P 1 + T P 2 + T P 3 + … + F N 1 + F N 2 + F N 3 + … Recall_{all}=\frac{TP_1+TP_2+TP_3+…}{TP_1+TP_2+TP_3+…+FN_1+FN_2+FN_3+…} R e c a l l a l l = T P 1 + T P 2 + T P 3 + … + F N 1 + F N 2 + F N 3 + … T P 1 + T P 2 + T P 3 + …
P r e c i s i o n a l l = T P 1 + T P 2 + T P 3 + … T P 1 + T P 2 + T P 3 + … + F P 1 + F P 2 + F P 3 + … Precision_{all}=\frac{TP_1+TP_2+TP_3+…}{TP_1+TP_2+TP_3+…+FP_1+FP_2+FP_3+…} P r e c i s i o n a l l = T P 1 + T P 2 + T P 3 + … + F P 1 + F P 2 + F P 3 + … T P 1 + T P 2 + T P 3 + …
m i c r o − F 1 s c o r e = 2 ∗ R e c a l l a l l ∗ P r e c i s i o n a l l R e c a l l a l l + P r e c i s i o n a l l micro-F1score=2*\frac{Recall_{all}*Precision_{all}}{Recall_{all}+Precision_{all}} m i c r o − F 1 s c o r e = 2 ∗ R e c a l l a l l + P r e c i s i o n a l l R e c a l l a l l ∗ P r e c i s i o n a l l
1 2 3 4 5 6 7 8 9 10 11 12 13 >>> from sklearn.metrics import f1_score >>> from sklearn.metrics import precision_recall_fscore_support >>> y_true = [0, 1, 2, 2, 1, 0] >>> y_pred = [0, 2, 1, 0, 1, 0] >>> f1_score(y_true,y_pred,average='micro' ) 0.5 >>> f1_score(y_true,y_pred,average='macro' ) 0.43333333333333335 >>> p_class, r_class, f_class, support_micro = precision_recall_fscore_support(y_true,y_pred,labels=[0,1,2]) >>> p_class, r_class, f_class (array([0.66666667, 0.5 , 0. ]), array([1. , 0.5, 0. ]), array([0.8, 0.5, 0. ])) >>> support_micro array([2, 2, 2])
衡量两个集合的相似度一种指标, 两个集合交集元素在并集中所占的比例 J ( y i , y ^ i ) = ∣ y i ∩ y ^ i ∣ ∣ y i ∪ y ^ i ∣ J\left(y_{i}, \hat{y}_{i}\right)=\frac{\left|y_{i} \cap \hat{y}_{i}\right|}{\left|y_{i} \cup \hat{y}_{i}\right|} J ( y i , y ^ i ) = ∣ y i ∪ y ^ i ∣ ∣ y i ∩ y ^ i ∣
1 2 3 4 5 6 7 8 9 10 11 12 13 14 >>> import numpy as np >>> from sklearn.metrics import jaccard_score >>> y_true = np.array([[0 , 1 , 1 ], ... [1 , 1 , 0 ]]) >>> y_pred = np.array([[1 , 1 , 1 ], ... [1 , 0 , 0 ]]) >>> jaccard_score(y_true[0 ], y_pred[0 ]) 0.6666 ... >>> jaccard_score(y_true, y_pred, average='samples' ) 0.5833 ... >>> jaccard_score(y_true, y_pred, average='macro' ) 0.6666 ... >>> jaccard_score(y_true, y_pred, average=None ) array([0.5 , 0.5 , 1. ])
用作衡量二元(两类)分类质量的指标。它考虑了真假阳性和阴性,通常被认为是一种平衡的度量,即使类的大小非常不同,也可以使用它,二分类计算公式如下: M C C = t p × t n − f p × f n ( t p + f p ) ( t p + f n ) ( t n + f p ) ( t n + f n ) . MCC = \frac{tp \times tn - fp \times fn}{\sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}. M C C = ( t p + f p ) ( t p + f n ) ( t n + f p ) ( t n + f n ) t p × t n − f p × f n .
MCC 本质上是 - 1 和 + 1 之间的相关系数值。+1 的系数表示完美预测,0 表示平均随机预测,-1 表示逆预测。该统计量也称为 phi 系数 1 2 3 4 5 >>> from sklearn.metrics import matthews_corrcoef >>> y_true = [+1, +1, +1, -1] >>> y_pred = [+1, -1, +1, +1] >>> matthews_corrcoef(y_true, y_pred) -0.33...
ROC 是 0.0 到 1.0 之间许多不同候选阈值的误报率(x 轴)与真阳性率(y 轴)的图。换句话说,它绘制了误报率与查全率 (漏报) 的关系 横座标:假阳率 (FPR) 纵座标: 真正率 / 查全率 (TPR) F P R = F P N = F P F P + T N T P R = T P P = T P T P + F N \begin{array}{l} FPR=\frac{FP}{N}=\frac{FP}{FP+TN} \\ TPR=\frac{TP}{P}=\frac{TP}{TP+FN}\end{array} F P R = N F P = F P + T N F P T P R = P T P = T P + F N T P
1 2 3 4 5 6 7 8 9 >>> from sklearn.metrics import roc_curve,roc_auc_score >>> y=[1,1,2,2] >>> score=[0.1,0.4,0.35,0.8] >>> fpr,tpr,thresholds=roc_curve(y,score,pos_label=2) >>> fpr,tpr,thresholds (array([0. , 0. , 0.5, 0.5, 1. ]), array([0. , 0.5, 0.5, 1. , 1. ]), array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])) >>> auc=roc_auc_score(y,score) >>> auc 0.75
点 (0,1):即 FPR=0, TPR=1,意味着 FN=0 且 FP=0,将所有的样本都正确分类 点 (1,0):即 FPR=1,TPR=0,最差分类器,避开了所有正确答案 点 (0,0):即 FPR=TPR=0,FP=TP=0,分类器把每个实例都预测为负类 点 (1,1):分类器把每个实例都预测为正类 一种会考虑所有可能分类阈值的评估指标 计算 :ROC 曲线下的面积 (又称 ROC 的积分),通常大于 0.5 小于 1,即随机挑选一个正样本以及一个负样本,分类器判定正样本的值高于负样本的概率就是 AUC 值AUC = 1,代表完美分类器 0.5 < AUC < 1,优于随机分类器 0 < AUC < 0.5,差于随机分类器 1 2 3 4 5 6 7 8 9 >>> from sklearn.metrics import roc_curve,roc_auc_score >>> y=[1 ,1 ,2 ,2 ] >>> score=[0.1 ,0.4 ,0.35 ,0.8 ] >>> fpr,tpr,thresholds=roc_curve(y,score,pos_label=2 ) >>> fpr,tpr,thresholds (array([0. , 0. , 0.5 , 0.5 , 1. ]), array([0. , 0.5 , 0.5 , 1. , 1. ]), array([1.8 , 0.8 , 0.4 , 0.35 , 0.1 ])) >>> auc=roc_auc_score(y,score) >>> auc 0.75
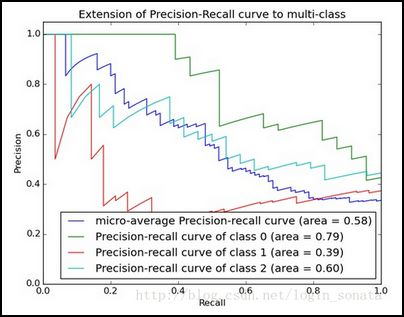
PR 曲线 ROC 是 0.0 到 1.0 之间许多不同候选阈值的真阳性率(x 轴)与查准率(y 轴)的图。换句话说,它绘制了查全率 (1 - 漏报) 与查准率(1 - 误报)的关系 横座标:真正率 / 查全率 (TPR) 纵座标: 查准率 (Precision) R e c a l l = T P P = T P T P + F N P r e c i s i o n = T P T P + F P \begin{array}{l}Recall=\frac{TP}{P}=\frac{TP}{TP+FN}\\ Precision=\frac{TP}{TP+FP}\end{array} R e c a l l = P T P = T P + F N T P P r e c i s i o n = T P + F P T P
PR 曲线的绘制原理看绘制 PR 曲线的原理?,使用 sklearn 可以快速得到 PR 曲线 1 2 3 4 5 6 7 from sklearn.metrics import precision_recall_curve,average_precision_scorenum=100 predict_scores=np.random.rand(num) eval_labels=np.random.randint(0 ,2 ,(num)) precision, recall, thresholds = precision_recall_curve(eval_labels, predict_scores)
PR 曲线指某个类别 的预测效果,绘制主要在于获得一组有顺序 的 PR 值对,所谓有顺序,PR 曲线从左到右进行绘制。实际使用时,按照 box 预测置信度从高到低的顺序求 PR 值对 1)按照 box 预测置信度降序排序 2)新加一个预测 box,根据 IOU 阈值统计当前加入的所有 box 的 TP、FP、FN 值,并计算 P、R 值 3)加完所有预测 box,得到一批 P、R 值,按顺序绘制到座标上,得到 PR 曲线 平均精度 (Average Precision) 是指 PR 曲线下的面积,通常使用一定数量的点对应的 Precision 求平均得到,这个面积的数值不会大于 1。PR 曲线下的面积越大,模型性能则越好 平均精度 (AP) 是按类计算的 ,需要借助其他指标(如 IoU、置信度、混淆矩阵(TP、FP、FN)、精度和召回率等)进行计算的AP 值的计算有 2 种方法,分别是:插值计算 AP (Interpolated average precision)、矩形近似计算 AP (Interpolated average precision),以下是 sklearn 的计算方法 1 2 3 4 5 6 7 8 9 from sklearn.metrics import precision_recall_curve,average_precision_scorenum=100 predict_scores=np.random.rand(num) eval_labels=np.random.randint(0 ,2 ,(num)) precision, recall, thresholds = precision_recall_curve(eval_labels, predict_scores) average_precision = average_precision_score(eval_labels, predict_scores)
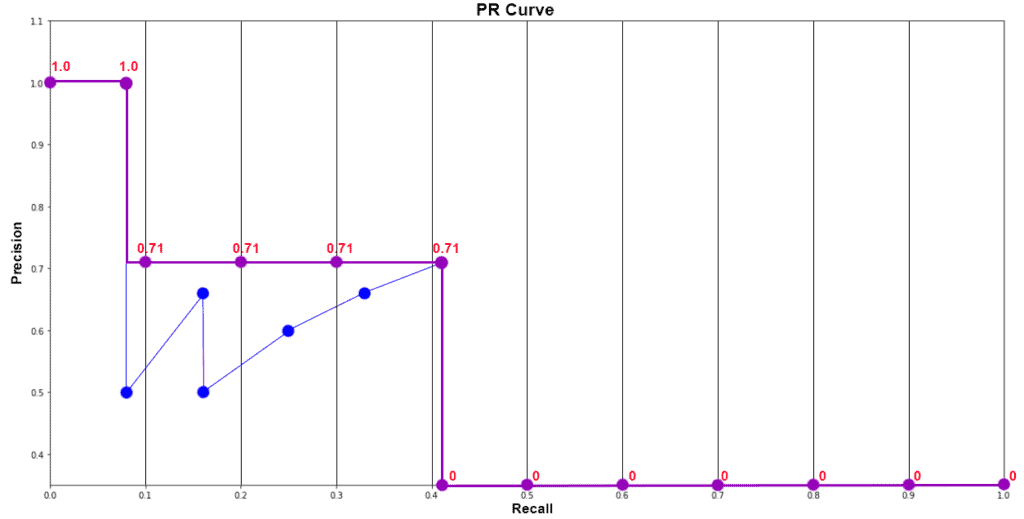
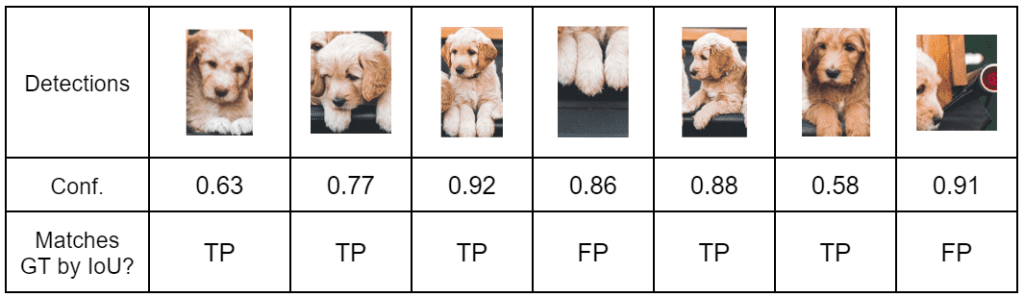
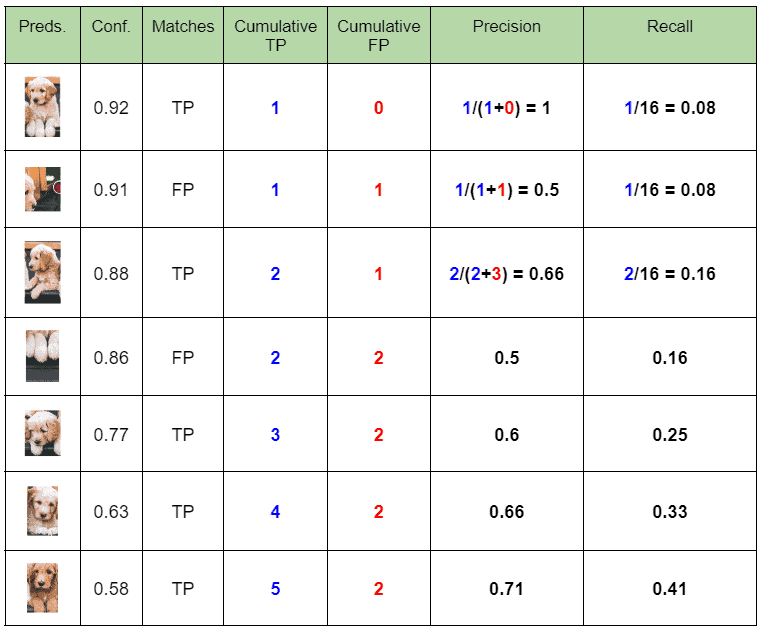
(1) 记录每个狗的检测以及置信度分数 (2) 计算精度和召回率: 先按置信度进行降序排序,然后累积 TP、FP,最后按行计算精度和召回率 (3) 绘制精度 - 召回率图: 如果表中包含相同召回值的多个精度值,则可以考虑最大值并丢弃其余值。不这样做不会影响 最终结果 (4) 使用 PASCAL VOC 11 点插值法计算平均精度 (AP): 精度值在 11 个召回值之间进行插值,即 0、0.1、0.2、0.3,…, 1.0。插值精度是对应于召回率值大于当前召回值的最大精度 。简单来说,它是右边的最大精度值。然后使用以下公式计算 A P = 1 / 11 ∗ S u m ( 11 − p o i n t ) = 1 / 11 ∗ ( 1 + 4 ∗ 0.71 + 6 ∗ 0 ) = 0.349 AP = 1/11 * Sum(11-point)=1/11*(1+4*0.71+6*0)=0.349 A P = 1 / 1 1 ∗ S u m ( 1 1 − p o i n t ) = 1 / 1 1 ∗ ( 1 + 4 ∗ 0 . 7 1 + 6 ∗ 0 ) = 0 . 3 4 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def cal_ap (prec,rec ): ap = 0. for t in np.arange(0. , 1.1 , 0.1 ): if np.sum (rec >= t) == 0 :p = 0 else :p = np.max (prec[rec >= t]) ap = ap + p / 11. return ap num=1000 prec=np.random.rand(num) rec=np.random.rand(num) cal_ap(prec,rec)
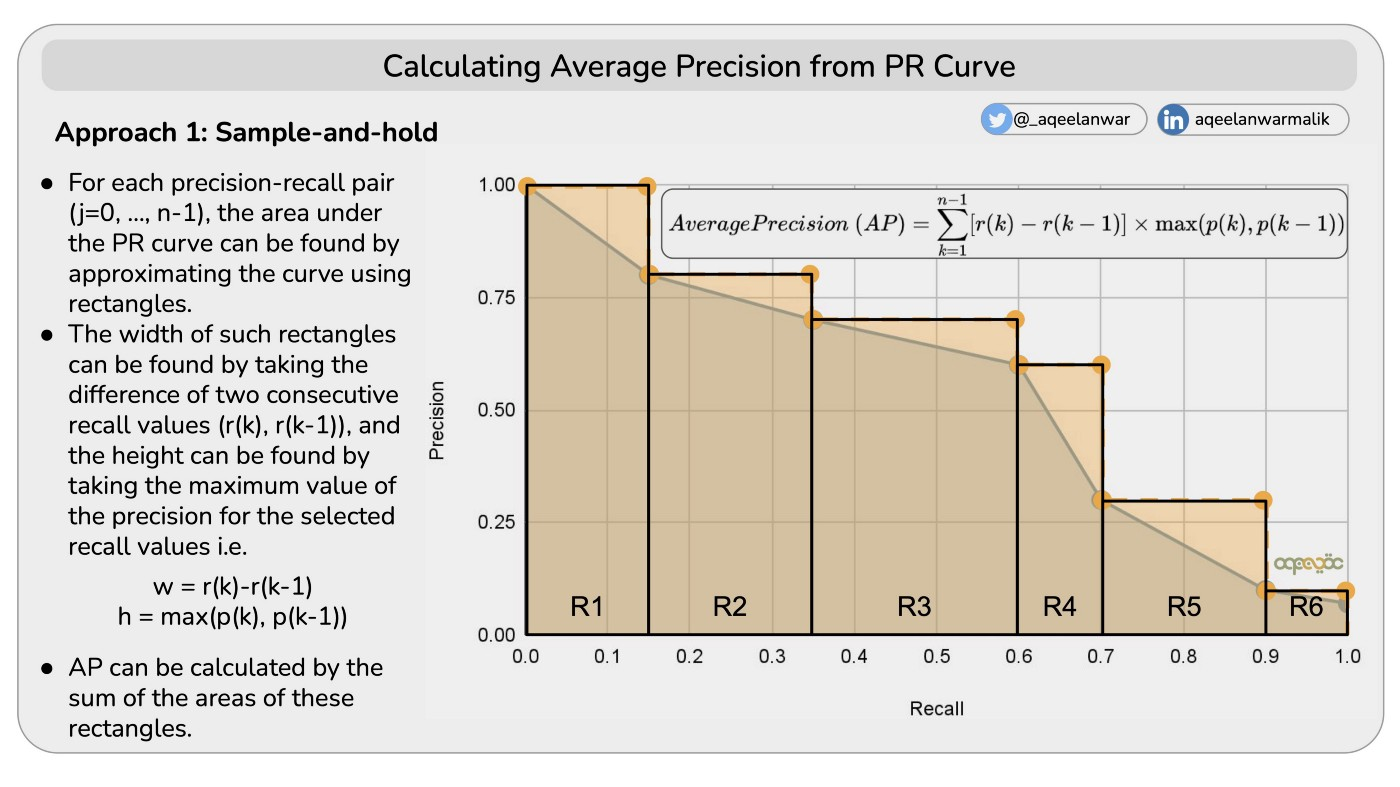
对于每个精度召回率对(j=0, …, n-1),可以通过使用矩形近似曲线来找到 PR 曲线下的面积 A P = ∑ n ( R n − R n − 1 ) P n \mathrm{AP}=\sum_{n}\left(R_{n}-R_{n-1}\right) P_{n} A P = n ∑ ( R n − R n − 1 ) P n
这种矩形的宽度可以通过取两个连续召回值 r (k),r (k-1) 的差值来找到,高度可以通过取所选召回值的精度的最大值来找到,即 w = r (k) - r (k-1),h = max (p (k),p (k-1)) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def cal_ap (rec, prec ): mrec = np.concatenate(([0. ], rec, [1. ])) mpre = np.concatenate(([0. ], prec, [0. ])) for i in range (mpre.size - 1 , 0 , -1 ): mpre[i - 1 ] = np.maximum(mpre[i - 1 ], mpre[i]) i = np.where(mrec[1 :] != mrec[:-1 ])[0 ] ap = np.sum ((mrec[i + 1 ] - mrec[i]) * mpre[i + 1 ]) return ap num=1000 prec=np.random.rand(num) rec=np.random.rand(num) pr=[[prec[i],rec[i]] for i in range (num)] pr=sorted (pr,key=lambda x:x[1 ],reverse=True ) cal_ap(np.array(pr)[0 ,:],np.array(pr)[1 ,:])
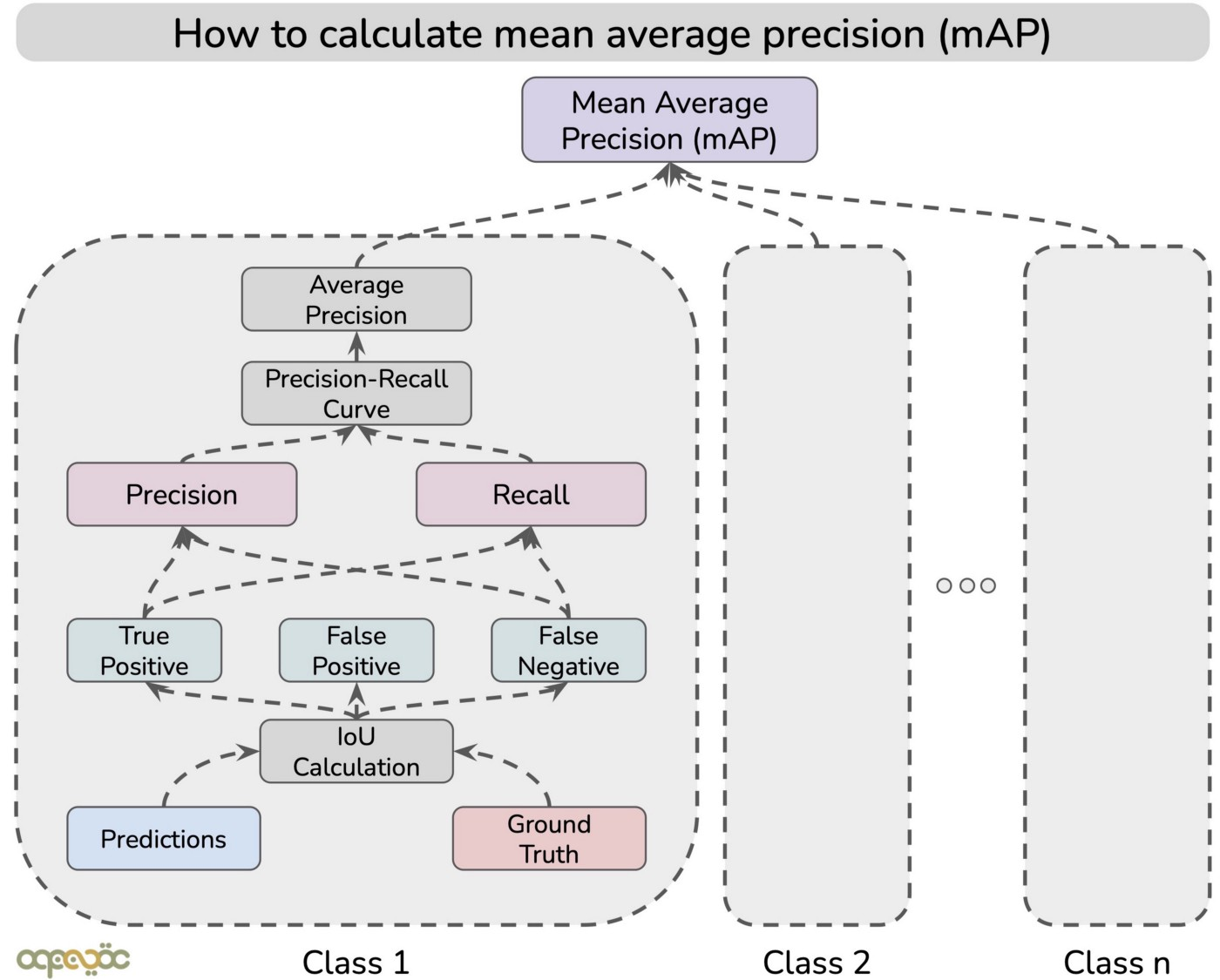
MAP 计算分成如下两步:(1) 计算某一类别的 AP 值;(2) mAP:所有类别 AP 值的平均 (1) 计算精度和召回率: 先按置信度进行降序排序,然后累积 TP、FP,最后按行计算精度和召回率 (2) 绘制精度 - 召回率图: 如果表中包含相同召回值的多个精度值,则可以考虑最大值并丢弃其余值。不这样做不会影响 最终结果 (3) 使用 PASCAL VOC 11 点插值法计算平均精度 (AP): 精度值在 11 个召回值之间进行插值,即 0、0.1、0.2、0.3,…, 1.0。插值精度是对应于召回率值大于当前召回值的最大精度 。简单来说,它是右边的最大精度值。然后使用以下公式计算 A P = 1 / 11 ∗ S u m ( 11 − p o i n t ) = 1 / 11 ∗ ( 1 + 4 ∗ 0.71 + 6 ∗ 0 ) = 0.349 AP = 1/11 * Sum(11-point)=1/11*(1+4*0.71+6*0)=0.349 A P = 1 / 1 1 ∗ S u m ( 1 1 − p o i n t ) = 1 / 1 1 ∗ ( 1 + 4 ∗ 0 . 7 1 + 6 ∗ 0 ) = 0 . 3 4 9
(4) 计算 mAP :按照以上方式计算所有类别的 AP 值,然后求平均 m A P = 1 / 5 ∗ ( 0.349 + 0.545 + 0.00 + 1.00 + 0.50 ) = 0.47 mAP=1/5*(0.349+0.545+0.00+1.00+0.50)=0.47 m A P = 1 / 5 ∗ ( 0 . 3 4 9 + 0 . 5 4 5 + 0 . 0 0 + 1 . 0 0 + 0 . 5 0 ) = 0 . 4 7
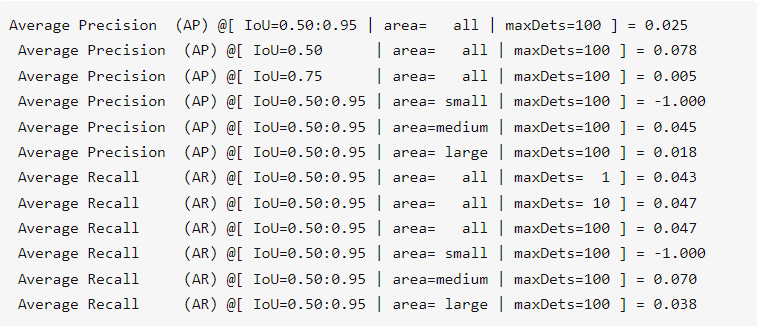
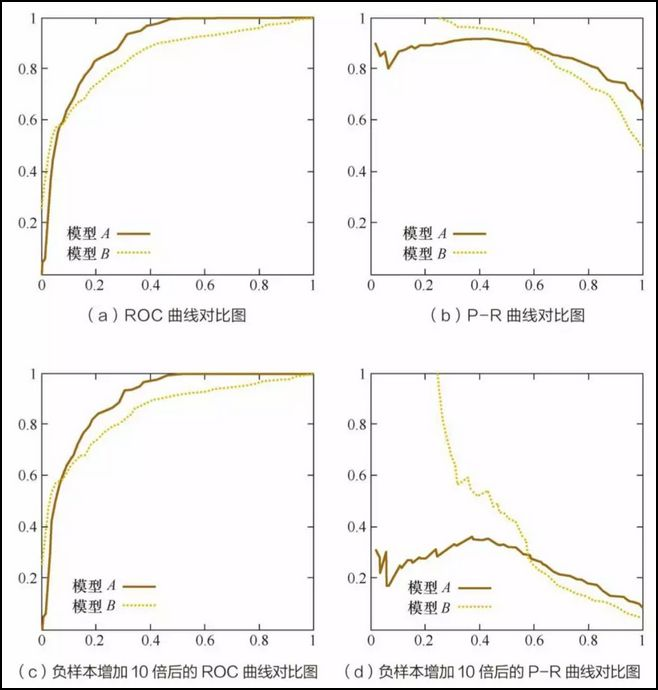
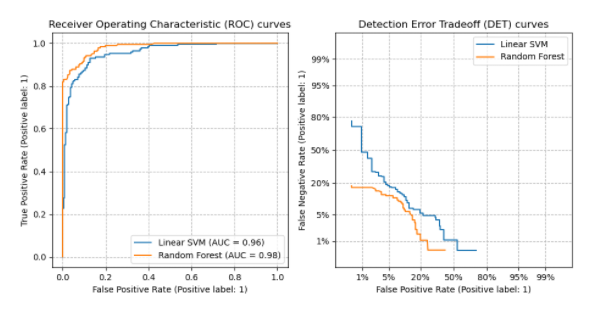
(1)VOC 2007 ,在 [0,1] 之间共计 11 个位置 Precision 的平均值 (2)VOC 2010 及以后 ,计算平滑后的 PR 曲线与 recall 轴围成的面积 (3)COCO ,设定多个 IOU 阈值(0.5-0.95,0.05 为步长),在每一个 IOU 阈值下都有某一类别的 AP 值,然后求不同 IOU 阈值下的 AP 平均,就是所求的最终的某类别的 AP 值 AP 值:准确率,你测到的 && 是真的 / 你测到的 AR 值:召回率,你测到的 && 是真的 / 是真的 IOU:交并比,用来判断东西是不是真的。比如你测到的 IoU=0.50 意味着 IoU 大于 0.5 被认为是检测到IoU=0.50:0.95 意味着 IoU 在 0.5 到 0.95 的范围内被认为是检测到限制 gt 框尺寸 : small 表示标注的框面积小于 32 * 32;medium 表示标注的框面积同时小于 96 * 96;large 表示标注的框面积大于等于 96 * 96;all 表示不论大小,都统计限制预测框数量 :maxDets=100 表示最大检测目标数为 100当每个类的观测值数量大致相等时,应使用 ROC 曲线 当存在中度到大型类不平衡时,应使用精度 - 召回率曲线 图中是 A、B 两个模型使用 ROC、PR 指标评估同一数据进行分类效果,可以看出负样本增加 10 倍后,PR 曲线出现波动 假如负样本增加 10 倍,FP、和 TN 的值均增大,对于横坐标而言,PR 的分母变小,而 ROC 的分子和分母同时变化,所以 ROC 曲线相对 PR 曲线更稳定 是二元分类系统错误率的图形图,绘制了错误拒绝率 与错误接受率 。X 轴和 y 轴通过其标准正态偏差(或仅通过对数变换)非线性缩放,产生比 ROC 曲线更线性的权衡曲线,并使用大部分图像区域来突出重要性的差异关键操作区域 DET 曲线是接受者操作特征 (ROC 曲线) 曲线的变体,其中假阴性率绘制在 y 轴上,而不是真阳性率 KS 曲线是两条线 ,其横轴是阈值,纵轴是召回率 (recall) 与假阳率 (FPR) 的值,值范围 [0,1] 。 KS 值:两条曲线之间之间相距最远的地方对应的阈值,就是最能划分模型的阈值 K S = max ( T P R − F P R ) K S=\max (T P R-F P R) K S = max ( T P R − F P R )
> 0.3 模型预测性较好 0.2~0.3 模型可用 0~0.2 模型预测能力较差 <0 模型错误 计算我们需要经过多大的排名分数才能覆盖所有真实标签。最佳值等于每个样本的 y_true 中的平均标签数 c o v e r a g e ( y , f ^ ) = 1 n samples ∑ i = 0 n samples − 1 max j : y i j = 1 rank i j coverage(y, \hat{f}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1} \max_{j:y_{ij} = 1} \text{rank}_{ij} c o v e r a g e ( y , f ^ ) = n samples 1 i = 0 ∑ n samples − 1 j : y i j = 1 max rank i j
1 2 3 4 5 6 >>> import numpy as np >>> from sklearn.metrics import coverage_error >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> coverage_error(y_true, y_score) 2.5
对于每个真实标签,排名较高的标签中有多少是真实标签?如果您能够为与每个样本关联的标签提供更好的排名,则此性能度量会更高。得到的分数总是严格大于 0,最佳值为 1 1 2 3 4 5 6 >>> import numpy as np >>> from sklearn.metrics import label_ranking_average_precision_score >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_average_precision_score(y_true, y_score) 0.416...
用于评价同一 object 在两种分类结果中是否被分到同一类别。现有真实类别列表 C 和聚类结果 K,a 表示在 C 与 K 中都是同类别的元素对数,b 表示在 C 与 K 中都是不同类别的元素对数,C 2 n C_2^n C 2 n R I = a + b C 2 n RI=\frac{a+b}{C_2^n} R I = C 2 n a + b 1 2 3 4 5 6 7 >>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2] >>> metrics.rand_score(labels_true, labels_pred) 0.66... >>> 3/6 0.66...
衡量两个分布的吻合程度,用于评价聚类结果 ,值越大表示聚类效果与真实情况越吻合,该度量方法有两种不同的标准化版本,标准化互信息 (NMI) 和调整互信息 (AMI) 假设 U, V 是 N 个目标的标签序列,他们各自的熵为 H (U)、H (V),MI (U, V) 为两者的互信息,其中 P ( i ) = ∣ U i ∣ / N , P ′ ( j ) = ∣ V i ∣ / N P(i)=|U_i|/N,P'(j)=|V_i|/N P ( i ) = ∣ U i ∣ / N , P ′ ( j ) = ∣ V i ∣ / N P ( i , j ) = ∣ U i ⋂ V j ∣ / N P(i,j)=|U_i \bigcap V_j|/N P ( i , j ) = ∣ U i ⋂ V j ∣ / N MI ( U , V ) = ∑ i = 1 ∣ U ∣ ∑ j = 1 ∣ V ∣ P ( i , j ) log ( P ( i , j ) P ( i ) P ′ ( j ) ) = H ( U ) + H ( V ) − H ( U , V ) H ( U ) = − ∑ i = 1 ∣ U ∣ P ( i ) log ( P ( i ) ) H ( V ) = − ∑ j = 1 ∣ V ∣ P ′ ( j ) log ( P ′ ( j ) ) \operatorname{MI}(U, V)=\sum_{i=1}^{|U|} \sum_{j=1}^{|V|} P(i, j) \log \left(\frac{P(i, j)}{P(i) P^{\prime}(j)}\right)=H(U)+H(V)-H(U,V)\\ H(U)=-\sum_{i=1}^{|U|} P(i) \log (P(i))\\ H(V)=-\sum_{j=1}^{|V|} P^{\prime}(j) \log \left(P^{\prime}(j)\right) M I ( U , V ) = i = 1 ∑ ∣ U ∣ j = 1 ∑ ∣ V ∣ P ( i , j ) log ( P ( i ) P ′ ( j ) P ( i , j ) ) = H ( U ) + H ( V ) − H ( U , V ) H ( U ) = − i = 1 ∑ ∣ U ∣ P ( i ) log ( P ( i ) ) H ( V ) = − j = 1 ∑ ∣ V ∣ P ′ ( j ) log ( P ′ ( j ) )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 >>> from sklearn import metrics >>> labels_true = [0 , 0 , 0 , 1 , 1 , 1 ] >>> labels_pred = [0 , 0 , 1 , 1 , 2 , 2 ] >>> metrics. Mutual_info_score (labels_true, labels_pred) 0.4620981203732969 >>> import math >>> H_true=-(3.0 /6 )*math.log(3.0 /6 )+(-(3.0 /6 )*math.log(3.0 /6 )) >>> H_true 0.6931471805599453 >>> H_pred=-(2.0 /6 )*math.Log (2.0 /6 )+(-(2.0 /6 )*math.Log (2.0 /6 ))+(-(2.0 /6 )*math.Log (2.0 /6 )) >>> H_pred 1.0986122886681096 >>> H_true_pred=-(1.0 /6 )*math.log(1.0 /6 )*2 -(2.0 /6 )*math.log(2.0 /6 )*2 >>> H_true_pred 1.3296613488547582 >>> H_true+H_pred-H_true_pred 0.4620981203732968
用于度量聚类结果的相似程度,是标准化的互信息 (Mutual Information, MI),其取值范围在 [0 1] 之间,值越大表示聚类结果越相近 NMI ( U , V ) = MI ( U , V ) mean ( H ( U ) , H ( V ) ) \operatorname{NMI}(U, V)=\frac{\operatorname{MI}(U, V)}{\operatorname{mean}(H(U), H(V))} N M I ( U , V ) = m e a n ( H ( U ) , H ( V ) ) M I ( U , V )
1 2 3 4 5 6 7 8 9 10 11 12 >>> labels_true = [0 , 0 , 0 , 1 , 1 , 1 ] >>> labels_pred = labels_true[:] >>> metrics.normalized_mutual_info_score(labels_true, labels_pred) 1.0 >>> import math >>> H_true=-(3.0 /6 )*math.log(3.0 /6 )+(-(3.0 /6 )*math.log(3.0 /6 )) >>> H_true 0.6931471805599453 >>> H_pred=H_true >>> MI_true_pred=metrics.mutual_info_score(labels_true, labels_pred) >>> MI_true_pred/((H_true+H_pred)/2 ) 0.999999999999999
对于随机结果,不能保证分数为 0,所以提出调整互信息,E [MI] 为互信息 (Mutual Information, MI) 的期望 A M I = M I − E [ M I ] mean ( H ( U ) , H ( V ) ) − E [ M I ] \mathrm{AMI}=\frac{\mathrm{MI}-E[\mathrm{MI}]}{\operatorname{mean}(H(U), H(V))-E[\mathrm{MI}]} A M I = m e a n ( H ( U ) , H ( V ) ) − E [ M I ] M I − E [ M I ]
1 2 3 4 5 >>> from sklearn import metrics >>> labels_true = [0 , 0 , 0 , 1 , 1 , 1 ] >>> labels_pred = [0 , 0 , 1 , 1 , 2 , 2 ] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) 0.22504 ...
用于评估聚类任务中真实标签未知的效果,定义两个中间量,a 表示任意一个点与同簇所有点的平均距离,b 表示任意一点与某一簇所有点的平均距离,则轮廓系数 (Silhouette Coefficient) 计算为: s = b − a max ( a , b ) s=\frac{b-a}{\max (a, b)} s = max ( a , b ) b − a
1 2 3 4 5 6 7 8 9 10 >>> from sklearn import metrics >>> from sklearn.metrics import pairwise_distances >>> from sklearn import datasets >>> X, y = datasets.load_iris(return_X_y=True ) >>> import numpy as np >>> from sklearn.cluster import KMeans >>> kmeans_model = KMeans(n_clusters=3 , random_state=1 ).fit(X) >>> labels = kmeans_model.labels_ >>> metrics.silhouette_score(X, labels, metric='euclidean' ) 0.55 ...
对于总样本有 n 个的聚类任务,样本 s 1 , s 2 , … , s n s_1,s_2,…,s_n s 1 , s 2 , … , s n n ∗ ( n − 1 ) / 2 n*(n-1)/2 n ∗ ( n − 1 ) / 2 TP:样本对在 GT 中是一个簇,同时在 Pred 中也是一个簇 FP:样本对在 Pred 中是一个簇,但是在 GT 中不是一个簇 FN:样本对在 GT 中是一个簇,但是在 Pred 中不是一个簇 TN:样本对在 GT 中不是一个簇,同时在 Pred 中也不是一个簇 FMI = TP ( TP + FP ) ( TP + FN ) \text { FMI }=\frac{\text { TP }}{\sqrt{(\text { TP }+\text { FP })(\text { TP }+\text { FN })}} FMI = ( TP + FP ) ( TP + FN ) TP 1 2 3 4 5 >>> from sklearn import metrics >>> labels_true = [0 , 0 , 0 , 1 , 1 , 1 ] >>> labels_pred = [0 , 0 , 1 , 1 , 2 , 2 ] >>> metrics. Fowlkes_mallows_score (labels_true, labels_pred) 0.47140 ...
同质性和完整性是用于评估衡量聚类算法聚类结果的两个标准。二者往往具有一定的负相关性 同质性:每一个 cluster (聚类结果簇) 中所包含的数据应归属于一个 class (类) 完整性:所有属于同一个 class 的数据应该被归到相同的 cluster 中 1 2 3 4 5 6 7 8 9 >>> from sklearn import metrics >>> labels_true = [0 , 0 , 0 , 1 , 1 , 1 ] >>> labels_pred = [0 , 0 , 1 , 1 , 2 , 2 ] >>> metrics. Homogeneity_score (labels_true, labels_pred) 0.66 ... >>> metrics.completeness_score(labels_true, labels_pred) 0.42 ... >>> metrics.v_measure_score(labels_true, labels_pred) 0.51 ...
兰德指数 (Rand index, RI) 不能保证在类别标签随机分配情况下,其值接近 0,为接近该问题提出调整兰德系数 ARI R I = R I − E [ R I ] m a x ( R I ) − E [ R I ] RI=\frac{RI-E[RI]}{max(RI)-E[RI]} R I = m a x ( R I ) − E [ R I ] R I − E [ R I ]
1 2 3 4 5 >>> from sklearn import metrics >>> labels_true = [0 , 0 , 0 , 1 , 1 , 1 ] >>> labels_pred = [0 , 0 , 1 , 1 , 2 , 2 ] >>> metrics.adjusted_rand_score(labels_true, labels_pred) 0.24 ...
评估聚类结果的指标,表示集群之间的平均 “相似性”,其中相似性是一个度量,用于比较集群之间的距离与集群本身的大小 假设一份数据,被分为 k 个聚簇,其中 s i s_i s i d i j d_{ij} d i j R i j R_{ij} R i j R i j = s i + s j d i j D B = 1 k ∑ i = 1 k max i ≠ j R i j R_{i j}=\frac{s_{i}+s_{j}}{d_{i j}}\\ D B=\frac{1}{k} \sum_{i=1}^{k} \max _{i \neq j} R_{i j} R i j = d i j s i + s j D B = k 1 i = 1 ∑ k i = j max R i j
1 2 3 4 5 6 7 8 9 >>> from sklearn import datasets >>> iris = datasets.load_iris() >>> X = iris.data >>> from sklearn.cluster import KMeans >>> from sklearn.metrics import davies_bouldin_score >>> kmeans = KMeans(n_clusters=3 , random_state=1 ).fit(X) >>> labels = kmeans.labels_ >>> davies_bouldin_score(X, labels) 0.6619 ...
所有簇间和簇内离散度之和之比 (其中离散度定义为距离的平方和) 计算公式s 为 ch 值,t r ( B k ) tr(B_k) t r ( B k ) t r ( W k ) tr(W_k) t r ( W k ) n E n_E n E c q c_q c q c E c_E c E 回归模型评价标准,在统计学中是指给定数据中的变异能被数学模型所解释的部分。通常会用方差来量化变异,故又称为可解释方差。 y , y ^ y,\hat y y , y ^ e x p l a i n e d _ v a r i a n c e ( y , y ^ ) = 1 − V a r { y − y ^ } V a r { y } explained\_{}variance(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}} e x p l a i n e d _ v a r i a n c e ( y , y ^ ) = 1 − V a r { y } V a r { y − y ^ }
1 2 3 4 5 6 7 8 9 10 11 >>> from sklearn.metrics import explained_variance_score >>> y_true = [3 , -0.5 , 2 , 7 ] >>> y_pred = [2.5 , 0.0 , 2 , 8 ] >>> explained_variance_score(y_true, y_pred) 0.957 ... >>> y_true = [[0.5 , 1 ], [-1 , 1 ], [7 , -6 ]] >>> y_pred = [[0 , 2 ], [-1 , 2 ], [8 , -5 ]] >>> explained_variance_score(y_true, y_pred, multioutput='raw_values' ) array([0.967 ..., 1. ]) >>> explained_variance_score(y_true, y_pred, multioutput=[0.3 , 0.7 ]) 0.990 ...
Max Error ( y , y ^ ) = m a x ( ∣ y i − y ^ i ∣ ) \text{Max Error}(y, \hat{y}) = max(| y_i - \hat{y}_i |) Max Error ( y , y ^ ) = m a x ( ∣ y i − y ^ i ∣ )
1 2 3 4 5 >>> from sklearn.metrics import max_error >>> y_true = [3 , 2 , 7 , 1 ] >>> y_pred = [9 , 2 , 7 , 1 ] >>> max_error(y_true, y_pred) 6
评价回归模型的标准,通过估计值与真实值的绝对误差衡量 MAE ( y , y ^ ) = 1 n samples ∑ i = 0 n samples − 1 ∣ y i − y ^ i ∣ . \text{MAE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \left| y_i - \hat{y}_i \right|. MAE ( y , y ^ ) = n samples 1 i = 0 ∑ n samples − 1 ∣ y i − y ^ i ∣ .
MAE 虽能较好衡量回归模型的好坏,但是绝对值的存在导致函数不光滑,在某些点上不能求导,可以考虑将绝对值改为残差的平方,这就是均方误差 (MSE, Mean Squared Error) 1 2 3 4 5 6 7 8 9 10 11 12 13 >>> from sklearn.metrics import mean_absolute_error >>> y_true = [3 , -0.5 , 2 , 7 ] >>> y_pred = [2.5 , 0.0 , 2 , 8 ] >>> mean_absolute_error(y_true, y_pred) 0.5 >>> y_true = [[0.5 , 1 ], [-1 , 1 ], [7 , -6 ]] >>> y_pred = [[0 , 2 ], [-1 , 2 ], [8 , -5 ]] >>> mean_absolute_error(y_true, y_pred) 0.75 >>> mean_absolute_error(y_true, y_pred, multioutput='raw_values' ) array([0.5 , 1. ]) >>> mean_absolute_error(y_true, y_pred, multioutput=[0.3 , 0.7 ]) 0.85 ...
每个样本的平均平方损失。MSE 的计算方法是平方损失除以样本数 MSE ( y , y ^ ) = 1 n samples ∑ i = 0 n samples − 1 ( y i − y ^ i ) 2 . \text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2. MSE ( y , y ^ ) = n samples 1 i = 0 ∑ n samples − 1 ( y i − y ^ i ) 2 .
1 2 3 4 5 6 7 8 9 >>> from sklearn. Metrics import mean_squared_error >>> y_true = [3 , -0.5 , 2 , 7 ] >>> y_pred = [2.5 , 0.0 , 2 , 8 ] >>> mean_squared_error (y_true, y_pred) 0.375 >>> y_true = [[0.5 , 1 ], [-1 , 1 ], [7 , -6 ]] >>> y_pred = [[0 , 2 ], [-1 , 2 ], [8 , -5 ]] >>> mean_squared_error(y_true, y_pred) 0.7083 ...
不希望在预测值和真值都是巨大数字时惩罚预测值和实际值的巨大差异时,通常使用 RMSLE,均方根对数误差便向预测值大值的(因为惩罚小值) MSLE ( y , y ^ ) = 1 n samples ∑ i = 0 n samples − 1 ( log e ( 1 + y i ) − log e ( 1 + y ^ i ) ) 2 . \text{MSLE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (\log_e (1 + y_i) - \log_e (1 + \hat{y}_i) )^2. MSLE ( y , y ^ ) = n samples 1 i = 0 ∑ n samples − 1 ( log e ( 1 + y i ) − log e ( 1 + y ^ i ) ) 2 .
1 2 3 4 5 6 7 8 9 >>> from sklearn.metrics import mean_squared_log_error >>> y_true = [3 , 5 , 2.5 , 7 ] >>> y_pred = [2.5 , 5 , 4 , 8 ] >>> mean_squared_log_error(y_true, y_pred) 0.039 ... >>> y_true = [[0.5 , 1 ], [1 , 2 ], [7 , 6 ]] >>> y_pred = [[0.5 , 2 ], [1 , 2.5 ], [8 , 8 ]] >>> mean_squared_log_error(y_true, y_pred) 0.044 ...
也称为平均绝对百分比偏差(MAPD),是回归问题的评估指标。这个度量的想法是对相对误差敏感。ϵ \epsilon ϵ 1 2 3 4 5 >>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [1 , 10 , 1e6 ] >>> y_pred = [0.9 , 15 , 1.2e6 ] >>> mean_absolute_percentage_error(y_true, y_pred) 0.2666 ...
通过取目标和预测之间的所有绝对差的中值来计算的,假设 y ^ \hat y y ^ 1 2 3 4 5 >>> from sklearn.metrics import median_absolute_error >>> y_true = [3 , -0.5 , 2 , 7 ] >>> y_pred = [2.5 , 0.0 , 2 , 8 ] >>> median_absolute_error(y_true, y_pred) 0.5
表示模型中的自变量已解释的方差(y)的比例。它提供了拟合优度的指示,因此通过解释方差的比例来衡量模型预测未见样本的可能性,假设 y ^ \hat y y ^ y y y 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 >>> from sklearn.metrics import r2_score >>> y_true = [3 , -0.5 , 2 , 7 ] >>> y_pred = [2.5 , 0.0 , 2 , 8 ] >>> r2_score(y_true, y_pred) 0.948 ... >>> y_true = [[0.5 , 1 ], [-1 , 1 ], [7 , -6 ]] >>> y_pred = [[0 , 2 ], [-1 , 2 ], [8 , -5 ]] >>> r2_score(y_true, y_pred, multioutput='variance_weighted' ) 0.938 ... >>> y_true = [[0.5 , 1 ], [-1 , 1 ], [7 , -6 ]] >>> y_pred = [[0 , 2 ], [-1 , 2 ], [8 , -5 ]] >>> r2_score(y_true, y_pred, multioutput='uniform_average' ) 0.936 ... >>> r2_score(y_true, y_pred, multioutput='raw_values' ) array([0.965 ..., 0.908 ...]) >>> r 2_score (y_true, y_pred, multioutput=[0.3 , 0.7 ]) 0.925 ...
计算解释的偏差百分比。它是 R² 的推广,其中平方误差被 Tweedie 偏差所取代。D²,也称为麦克法登似然比指数 D 2 ( y , y ^ ) = 1 − D ( y , y ^ ) D ( y , y ˉ ) . D^2(y, \hat{y}) = 1 - \frac{\text{D}(y, \hat{y})}{\text{D}(y, \bar{y})} \,. D 2 ( y , y ^ ) = 1 − D ( y , y ˉ ) D ( y , y ^ ) .
像 R² 一样,最好的分数是 1.0,它可以是负数(因为模型可以任意变差)。始终预测 y 的期望值的常量模型,不考虑输入特征,将获得 0.0 的 D² 分数 1 2 >>> from sklearn. Metrics import d 2_tweedie_score, make_scorer>>> d2_tweedie_score_15 = make_scorer(d2_tweedie_score, power=1.5 )
使用参数计算平均 Tweedie 偏差误差 power (),这是一个引出回归目标的预测期望值的度量 当 power=0 它相当于均方误差 (MSE, Mean Squared Error) 当 power=1 它相当于 mean_poisson_deviance 当 power=2 它相当于 mean_gamma_deviance 1 2 3 4 5 6 7 8 9 10 11 12 13 >>> from sklearn.metrics import mean_tweedie_deviance >>> mean_tweedie_deviance([1.0 ], [1.5 ], power=0 ) 0.25 >>> mean_tweedie_deviance([100. ], [150. ], power=0 ) 2500.0 >>> mean_tweedie_deviance([1.0 ], [1.5 ], power=1 ) 0.18 ... >>> mean_tweedie_deviance([100. ], [150. ], power=1 ) 18.9 ... >>> mean_tweedie_deviance([1.0 ], [1.5 ], power=2 ) 0.14 ... >>> mean_tweedie_deviance([100. ], [150. ], power=2 ) 0.14 ...
用于评估分位数回归模型的预测性能。所述弹球损失相当于 mean_absolute_error 当位数参数 alpha 被设置为 0.5 pinball ( y , y ^ ) = 1 n samples ∑ i = 0 n samples − 1 α max ( y i − y ^ i , 0 ) + ( 1 − α ) max ( y ^ i − y i , 0 ) \text{pinball}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \alpha \max(y_i - \hat{y}_i, 0) + (1 - \alpha) \max(\hat{y}_i - y_i, 0) pinball ( y , y ^ ) = n samples 1 i = 0 ∑ n samples − 1 α max ( y i − y ^ i , 0 ) + ( 1 − α ) max ( y ^ i − y i , 0 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 >>> from sklearn.metrics import mean_pinball_loss >>> y_true = [1 , 2 , 3 ] >>> mean_pinball_loss(y_true, [0 , 2 , 3 ], alpha=0.1 ) 0.03 ... >>> mean_pinball_loss(y_true, [1 , 2 , 4 ], alpha=0.1 ) 0.3 ... >>> mean_pinball_loss(y_true, [0 , 2 , 3 ], alpha=0.9 ) 0.3 ... >>> mean_pinball_loss(y_true, [1 , 2 , 4 ], alpha=0.9 ) 0.03 ... >>> mean_pinball_loss(y_true, y_true, alpha=0.1 ) 0.0 >>> mean_pinball_loss(y_true, y_true, alpha=0.9 ) 0.0
语义分割常用的评价指标,指所有类别的 IOU 值平均就是 mIOU 首先统计某个类别在所有图片上的累计 TP、FP、FN 像素数量、然后计算这个类别的 IOU,不是针对每张图计算 IOU ,再算平均 参考文献:
![机器学习常见评价指标-20230704222045]()
![机器学习常见评价指标-20230704222046]()
![机器学习常见评价指标-20230704222047]()
![机器学习常见评价指标-20230704222048]() 计算结果如下
计算结果如下![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![机器学习常见评价指标-20230704222247]()
![]()
![]()
![]()
![机器学习常见评价指标-20230704222249]() $$I o U=\frac{T P}{F P+T P+F N}$$
$$I o U=\frac{T P}{F P+T P+F N}$$![机器学习常见评价指标-20230704222249-1]()

 计算结果如下
计算结果如下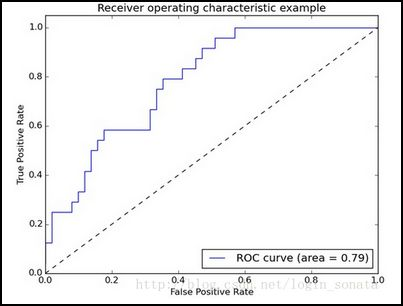





 $$I o U=\frac{T P}{F P+T P+F N}$$
$$I o U=\frac{T P}{F P+T P+F N}$$