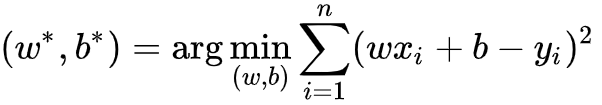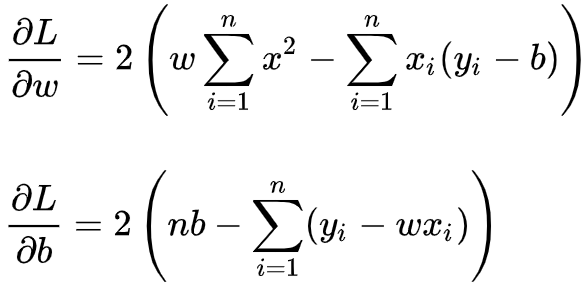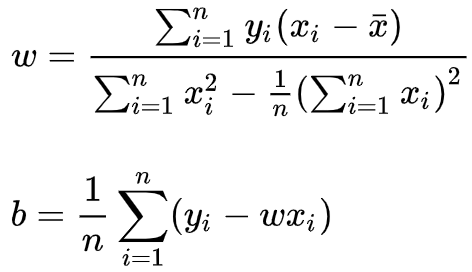普通最小二乘回归 - OLSR

最小二乘法，通过求导全局求解函数参数

什么是普通最小二乘模型 (OLS)？

• 最基础的线性模型，最小化数据集中观察到的目标与通过线性近似预测的目标之间的残差平方和，

  $$\min_{w} || X w - y||_2^2$$

  >>> from sklearn import linear_model
  >>> reg = linear_model.LinearRegression()
  >>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
      LinearRegression()
  >>> reg.coef_
      array([0.5, 0.5])

• 普通最小二乘法的系数估计依赖于特征的独立性。当特征相关且设计矩阵的列 X 具有近似线性相关性，设计矩阵变得接近奇异，因此，最小二乘估计对观察目标中的随机误差变得高度敏感，产生很大的方差

求解线性回归的目标函数的最小二乘法？

• 目标函数
• 分别对 w,b 求导
• 令两式为 0，解得

什么是非负最小二乘法？

• 将所有系数约束为非负数，这在它们表示一些物理或自然非负量（例如，频率计数或商品价格）时可能很有用

普通最小二乘法的复杂度？

• 使用 X 的奇异值分解计算最小二乘解。如果 X 是形状矩阵，则 此方法的成本为$O(n_{\text{samples}} n_{\text{features}}^2)$

极大似然估计和最小二乘法区别

• 对于最小二乘法，当从模型总体随机抽取 n 组样本观测值后，最合理的参数估计量应该使得模型能最好地拟合样本数据，也就是估计值和观测值之差的平方和最小
• 而对于最大似然法，当从模型总体随机抽取 n 组样本观测值后，最合理的参数估计量应该使得从模型中抽取该 n 组样本观测值的概率最大

最小均方误差（LMSE）和最小二乘法（LS）有什么区别与联系？

• 均方误差＝方差＋偏差的平方，当估计量无偏时，均方误差等于方差。所以，当满足最小二乘法条件且估计量是无偏估计量，那么求最小均方误差等价于最小二乘法
• 均方误差可以看作是加权的最小二乘法，其中的权值表示概率
• 

参考：

1. 如何理解最小二乘法？