HSSN：Deep Hierarchical Semantic Segmentation

发表于 更新于 分类于 ， 阅读次数： 本文字数： 4.4k 阅读时长 ≈ 4 分钟

HSSN抛弃传统的每个像素进行扁平分类的思想，在借鉴层次聚类的想法后，在网络输出端增加"类别树"约束，使得网络学习到的特征更加鲁棒

什么是 HSSN？

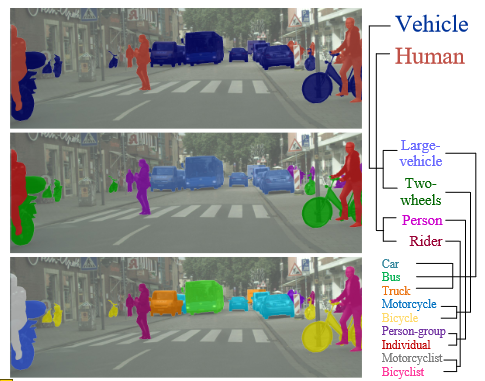
  • HSSN-20230408143142
  • 人类能够在观察中识别结构化关系，使我们能够将复杂的场景分解为更简单的部分，并在多个层次上抽象视觉世界。然而，人类感知的这种分层推理能力在当前的语义分割文献中仍然在很大程度上没有得到探索。现有工作通常知道扁平化标签，并专门针对每个像素预测目标类
  • 在本文中，我们讨论了分层语义分割（HSS），它旨在根据类层次结构对视觉观察进行结构化的像素级描述。我们设计了 HSSN，这是一个通用的 HSS 框架，解决了这项任务中的两个关键问题：i）如何有效地使现有的与层次结构无关的分段网络适应 HSS 设置，以及 ii）如何利用层次结构信息来规范 HSS 网络学习
  • 了解决第1个问题，HSSN直接将HSS视为一个像素级多标签分类问题，因此相比于现在的分割模型只引入了极小的改动，对于第2个问题，HSSN网络首先将探索语义层次作为训练目标，这将会迫使分割结果遵从语义结构，同时，通过施加类别间的边缘约束，HSSN将会对像素映射空间进行重新构造，最终产生更好的像素表示并提升模型的效果

HSSN 的网络结构？

  • Hierarchical Semantic Segmentation Networks：这一部分确保了类别的连贯性以及一致性（推测在取类别最大值的时候会做一些额外的处理，来确保所有取到的最大值都处于同一个类别树的分支上保证类别的连贯，但是作者在正文中没给出）
  • Hierarchy-Aware Segmentation Learning：
    • pixel-wise hierarchical segmentation learning strategy：像素级层次分割学习策略，确保预测能够在层次关系上保持一致
      • 每个像素分配的标签都应该具有层次上的一致性，因此需要遵守以下的两个原则 HSSN-20230408143142-1
      • Tree-Min Loss：如果子节点是对的，就取概率最小的节点路径（保证子节点要比父节点概率小，这条路径还没到当前的节点，也保证了之前的路径最短），如果子节点是错的，就取概率最大的节点路径（因为是错的取最大，最大最小一样的概率很小，所以就能够防止在这条路径上走下去，另外这条路径已经包括了当前的节点，或者说这条路径的最后一个节点就是当前这个节点）。相比于直接使用BCE Loss，Tree-Min Loss得出的score能确保完全符合作者设定的两个限制条件，并能够加大对不符合条件预测的惩罚
      • Focal Tree-Min Loss：受到focal Loss的启发，作者在其中增加了调节因子，以便能够对困难的例子更好的学习
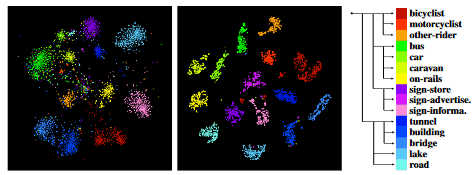
    • pixel-wise hierarchical representation learning strategy：像素级层次表示学习策略，确保在表示空间中能够将不同类别的表示有效地重构，从而学习到更好的表示。类似于对比学习，作者会挑选标准图、正样本、负样本三张图作为一组，通过多组计算损失，里面的参数 m 会迫使正负样本的距离超过 m HSSN-20230408143143

HSSN 如何更新预测分数的？

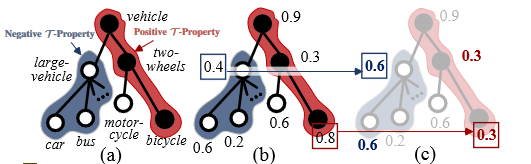
  • HSSN-20230408143143-1
  • 上图是计算图像某一个像素点类别时画出的树状图，图（a）中将正确的分类路径用红色标注出来，错误的用蓝色标注（实心代表 positive class，空心代表 negative class），图（b）则显示了相对应的 BCE 损失，作者将两个不合理的点单独做了标注（在数字上添加了方框），可以看到在使用 BCE Loss 时，第二层节点的损失是差不多的，图（c）则采用了作者的 LtmL^{tm} 损失（后面会提到，这个损失可以保证在计算时让每个点都符合作者给出的两个限制条件），能够成功地在不同类别上显示出区分性，保证模型训练的层次结构较为合理
  • 假设模型直接输出是 s，更新后是 p，其中 AvA_v 与 CvC_v 代表 vv 的父集和子类集，第二行也可以更新为 pv=max(su)p_v=max(s_u) ，按照以下公式更新得到图 c 的新分数

    {pv=min⁡u∈Av(su)ifl^v=1,1−pv=min⁡u∈Cv(1−su)=1−max⁡u∈Cv(su)ifl^v=0,\begin{cases}\quad p_v=\min\limits_{u\in\mathcal{A}_v}(s_u)&\text{if}\hat{l}_v=1,\\ 1-p_v=\min\limits_{u\in\mathcal{C}_v}(1-s_u)=1-\max\limits_{u\in\mathcal{C}_v}(s_u)&\text{if}\hat{l}_v=0,\end{cases}

  • 总结：在父节点 uu 往下辨别子节点 vv 时，如果子节点是对的，就取概率最小的节点路径（保证子节点要比父节点概率小，这条路径还没到当前的节点，也保证了之前的路径最短），如果子节点是错的，就取概率最大的节点路径（因为是错的取最大，最大最小一样的概率很小，所以就能够防止在这条路径上走下去，另外这条路径已经包括了当前的节点，或者说这条路径的最后一个节点就是当前这个节点）

HSSN 如何强制预测符合类别层次关系的？

  • HSSN-20230408143143
  • 挑选标准图、正样本、负样本三张图作为一组，通过多组计算损失，里面的参数 m 会迫使正负样本的距离超过 m，从而使得损失为0

    LTT(i,i+,i−)=max⁡{⟨i,i+⟩−⟨i,i−⟩+m,0},\mathcal{L}^{\mathrm{TT}}(\boldsymbol{i},\boldsymbol{i}^+,\boldsymbol{i}^-)=\max\{\langle\boldsymbol{i},\boldsymbol{i}^+\rangle-\langle\boldsymbol{i},\boldsymbol{i}^-\rangle+m,0\},

HSSN 的 TML 损失函数？

  • Tree-Min Loss：如果子节点是对的，就取概率最小的节点路径（保证子节点要比父节点概率小，这条路径还没到当前的节点，也保证了之前的路径最短），如果子节点是错的，就取概率最大的节点路径（因为是错的取最大，最大最小一样的概率很小，所以就能够防止在这条路径上走下去，另外这条路径已经包括了当前的节点，或者说这条路径的最后一个节点就是当前这个节点）。相比于直接使用 BCE Loss，Tree-Min Loss 得出的 score 能确保完全符合作者设定的两个限制条件，并能够加大对不符合条件预测的惩罚

    LTM(p)=∑v∈V−l^vlog⁡(pv)−(1−l^v)log⁡(1−pv),=∑v∈V−l^vlog⁡(min⁡u∈Av(su))−(1−l^v)log⁡(1−max⁡u∈Cv(su)).\begin{aligned}\mathcal{L}^{\mathtt{TM}}(p)&=\sum\limits_{v\in\mathcal{V}}-\hat{l}_v\log(p_v)-(1-\hat{l}_v)\log(1-p_v),\\ &=\sum\limits_{v\in\mathcal{V}}-\hat{l}_v\log(\min_{u\in\mathcal{A}_v}(s_u))-\\ &(1-\hat{l}_v)\log(1-\max_{u\in\mathcal{C}_v}(s_u)).\end{aligned}

  • Focal Tree-Min Loss：受到 focal Loss 的启发，作者在其中增加了调节因子，以便能够对困难的例子更好的学习

    LTM(p)=∑v∈P−l^v(1−pv)γlog⁡(pv)−(1−l^v)(pv)γlog⁡(1−pv),=∑v∈V−l^v(1−min⁡u∈Av(su))γlog⁡(min⁡u∈Av(su))−(1−l^v)(max⁡u∈Cv(su))γlog⁡(1−max⁡u∈Cv(su)),\begin{array}{l}\mathcal{L}^{\mathrm{TM}}(p)=\sum\limits_{v\in\mathcal{P}}-\hat{l}_v(1-p_v)^\gamma\log(p_v)-(1-\hat{l}_v)(p_v)^\gamma\log(1-p_v),\\ =\sum\limits_{v\in\mathcal{V}}-\hat{l}_v(1-\operatorname*{min}_{u\in\mathcal{A}_v}(s_u))^\gamma\log(\operatorname*{min}_{u\in A_v}(s_u))-(1-\hat{l}_v)(\max_{u\in\mathcal{C}_v}(s_u))^\gamma\log(1-\max_{u\in\mathcal{C}_v}(s_u)),\end{array}

HSSN 的 TTL 损失函数？

  • 挑选标准图、正样本、负样本三张图作为一组，通过多组计算损失，里面的参数 m 会迫使正负样本的距离超过 m，从而使得损失为0

    LTT(i,i+,i−)=max⁡{⟨i,i+⟩−⟨i,i−⟩+m,0},\mathcal{L}^{\mathrm{TT}}(\boldsymbol{i},\boldsymbol{i}^+,\boldsymbol{i}^-)=\max\{\langle\boldsymbol{i},\boldsymbol{i}^+\rangle-\langle\boldsymbol{i},\boldsymbol{i}^-\rangle+m,0\},

参考：
Papers - Deep Hierarchical Semantic Segmentation - 知乎