VAE

发表于 2023-12-09 更新于 2025-01-18 分类于 2-深度学习， B-视觉模型， 2-高级视觉任务GAN ，生成图片阅读次数：本文字数： 4.1k 阅读时长 ≈ 4 分钟

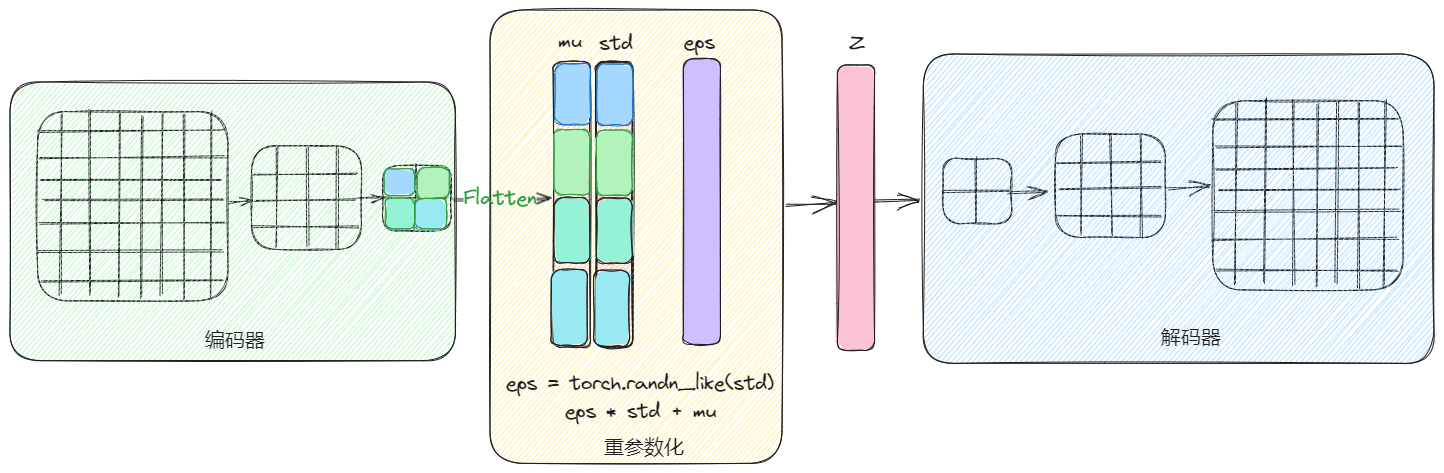
和 AE 生成样本的过程类似，但是引入对隐变量的约束，利用高斯混合模型 (GMM) 的概念去逼近真实样本的分布

什么是 VAE ？

假设我们有一批样本数据 $\{X_1, X_1,..., X_n\}$ ，类似全概率公式，生成模型的本质是为了得到等于或靠近分布 p (X)，如果能得到这个分布，输入任意随机变量就可以生成样本，但是这是不可能的。于是将分布改

p(X)=\sum_Z p(X|Z)p(Z)

也就是通过另一个随机变量 Z 去生成 X，并且假设 $p(Z)=\mathcal{N}(0,I)$ ，也就是先从标准正态分布采样一个 Z，然后根据 Z 去算 X
上图是先由 X 生成隐变量，然后通过采样方差和均值，生成服从正太分布的 Z，即通过多组正太分布的组合去逼近 X 的真实分布，这里使用了高斯混合模型 (GMM) 的概念

VAE 的重参数化技巧？

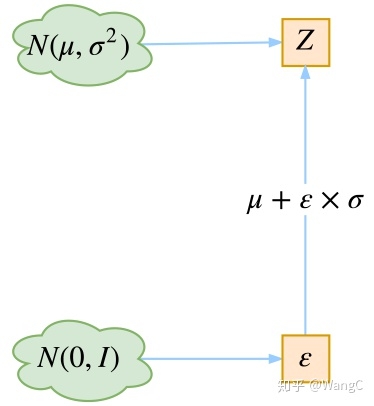
若希望从高斯分布 $N(\mu,\sigma^2)$ 中采样，可以先从标准分布 ${\cal N}(0,1)$ 采样出 z ，再得到 $\sigma*z+\mu$ ，这就是我们想要采样的结果。这样做的好处是将随机性转移到了 z 这个常量上，而 $\sigma$ 和 $\mu$ 则当作仿射变换网络的一部分

同样 VAE 已知正态分布采样得到隐变量 Z，但是直接采样无法实现梯度反向传播的，因此因此不通过

y\sim N(\mu,\sigma^2)

采样，而是使用

\epsilon\sim{\cal N}(0,1)

# 用标准正态分布采样任意高斯分布，假设输入是(N,m)
def noise_reparameterize(mean,logvar):
	# mean，logvar是N*m个高斯函数的均值和方差
	eps = torch.randn(mean.shape).to(device)
	z = mean + eps * torch.exp(logvar)
	return z

VAE 的损失函数？

(1) 已知模型输出分布计算如下：对 latency space 随机采样 m 个点，其中 m 服从多项式分布 $p(x)$ ，每采样一个点 m，将其对应到一个高斯分布 $N(\mu^{m},\sigma^{m})$ ，于是一个多项式分布利用高斯混合模型 GMM 可以表示

p(x)=\sum_mp(m)p(x\mid m)=\int_zp(z)p(x\mid z)dz

(2) VAE 训练目的：是使得以上尽可能大，

\begin{aligned}Maxinum\log p(x)& =\int_{z}q(z\mid x)\log p(x)dz \\&=\int_zq(z\mid x)\log\biggl(\frac{p(z,x)}{p(z\mid x)}\biggr)dz \\&=\int_{z}q(z\mid x)\log\biggl(\frac{p(z,x)}{q(z\mid x)}\frac{q(z\mid x)}{p(z\mid x)}\biggr)dz& \left(4\right) \\&=\int_zq(z\mid x)\log\biggl(\frac{p(z,x)}{q(z\mid x)}\biggr)dz+\int_zq(z\mid x)\log\biggl(\frac{q(z\mid x)}{p(z\mid x)}\biggr)dz \\&=\int_zq(z\mid x)\log\biggl(\frac{p(z,x)}{q(z\mid x)}\biggr)dz+KL(q(z\mid x)\Vert p(z\mid x))\end{aligned}

(3) 损失的下确界：公式右边的 KL 散度是一个 >=0 的部分，于是 $\log p(x)$ 的下确界由以上公式的左边定义，

\log p(x)\geq\int_zq(z\mid x)\log\biggl(\frac{p(x|z)p(z)}{q(z|x)}\biggr)dz

(4) 下确界分析：由下确界的定义可知，最大化 $log p(x)$ 等价于最大化下确界，

\begin{aligned}L_{b}& =\int_{z}q(z\mid x)\log\biggl(\frac{P(z,x)}{P(z\mid x)}\biggr)dz \\&=\int_zq(z\mid x)\log\biggl(\frac{P(x\mid z)P(z)}{q(z\mid x)}\biggr)dz \\&=\int_zq(z\mid x)\log\biggl(\frac{P(z)}{q(z\mid x)}\biggr)dz+\int_zq(z\mid x)\log P(x\mid z)dz \\&=-KL(q(z\mid x)\|P(z))+\int_zq(z\mid x)\log P(x\mid z)dz\end{aligned}

(5) 损失分析：以上公式左边是一个 KL 散度，表示的是生成的隐变量分布和隐变量先验分布的差距，其实就是生成的隐变量分布和标准正太分布的差距，由于是负值，所以需要最小化 KL 散度，也即隐变量分布和标准正太分布越接近越好。等式右边是重建损失，表示期望 Encoder 输出 $q(z|x)$ 的情况下 Decoder 输出 p (x|z) 尽可能的大。即需要从编码器 Encoder 得到的隐变量空间中采样隐变量 z，对采样得到的隐变量 z 进行解码 Decoder，使得解码得到的 $\hat x$ 分布中，对应是输入 x 的概率尽可能

\text{Maximum}\int_zq(z\mid x)\log p(x\mid z)dz=\text{Maximum}E_{q(z\mid x)}[\log p(x\mid z)]

总的来说，VAE 以最大化对数似然的下界（Evidence Lower Bound，ELBO） 为目的，通过 KL 散度和重建损失完成模型的训练

VAE 与 AE 的区别？

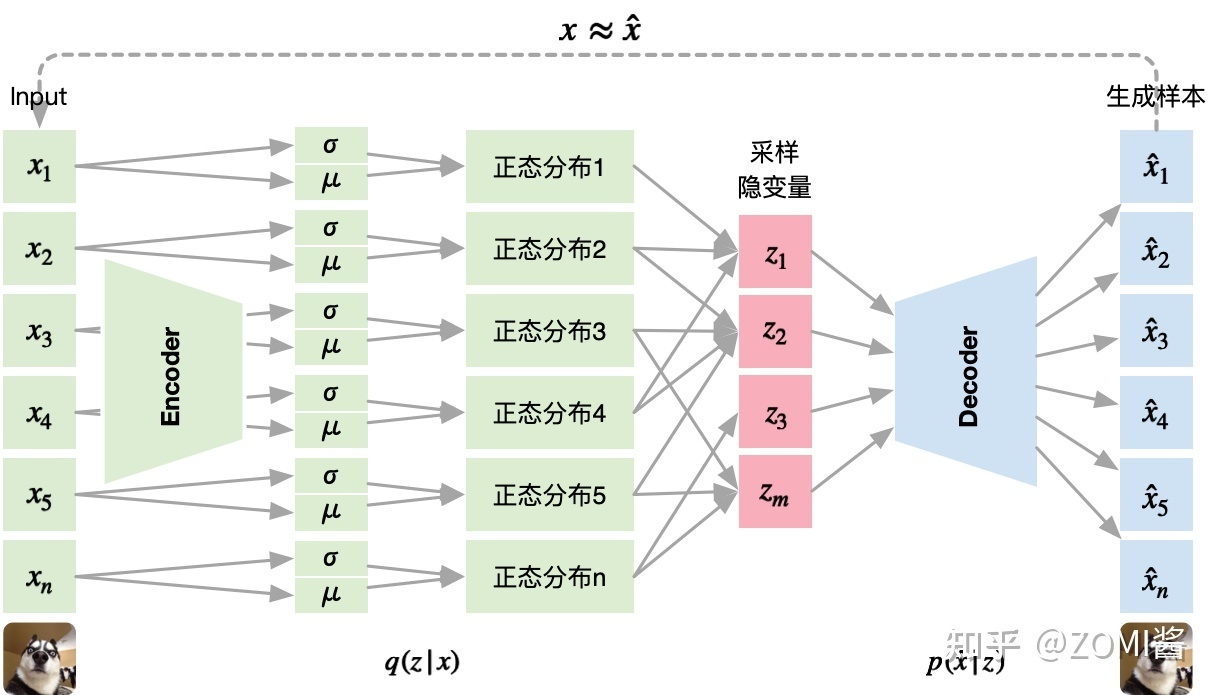
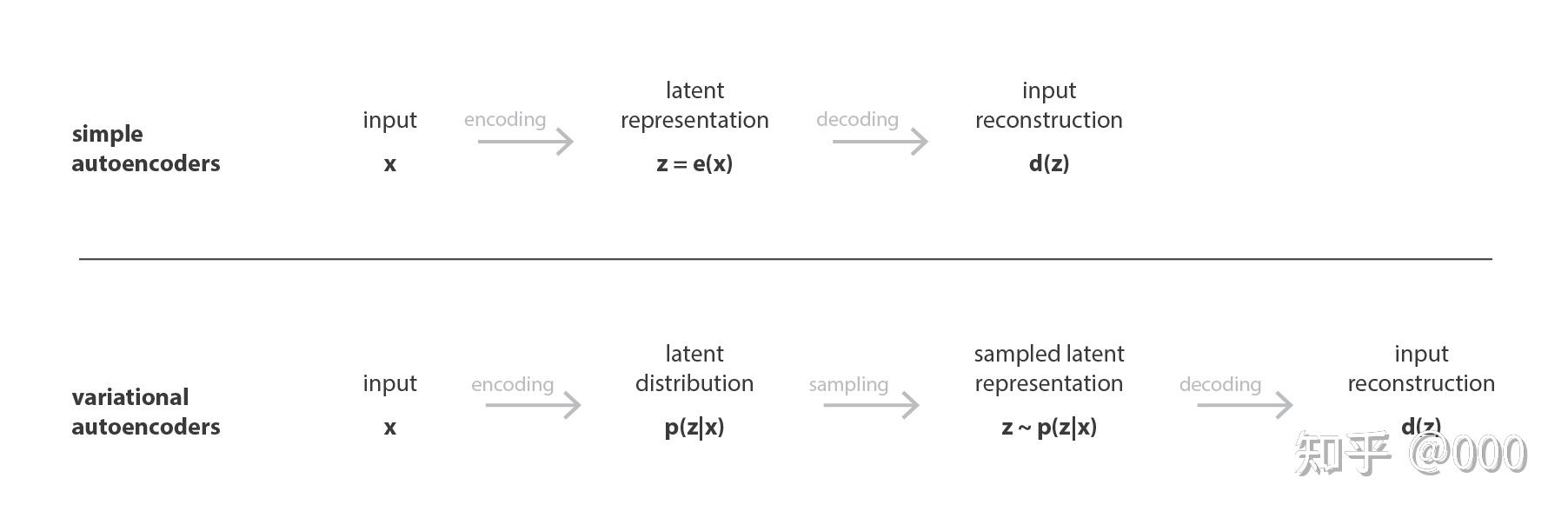
与自编码器是直接生成确定隐变量 z 不同，在 VAE 中，encoder 输出隐向量 z 的分布的均值 μ 与标准差 σ，再从这个分布中采样得到隐向量 z。
换句话说，AE 将输入 encode 成隐空间里的单个点，而 VAE 则是将输入 encode 成隐空间里的分布 (distribution)
AE 更容易过拟合训练过的数据，对没见过的数据生成效果差。而 VAE 直接学习原始数据隐空间的分布，其隐变量鲁棒性更强

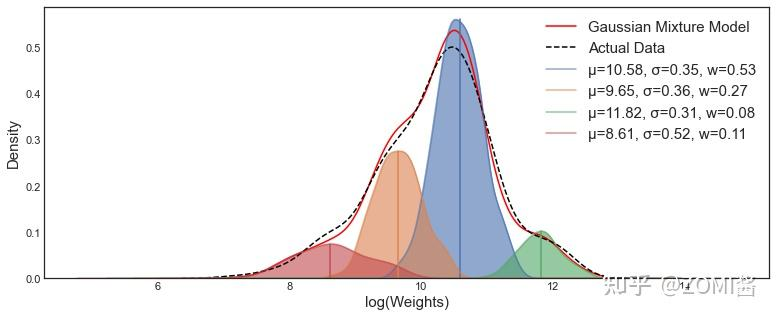
什么是高斯混合模型 GMM？

一种聚类算法，通过多个高斯分布函数的线性组合，理论上可以逼近任意类型的分布。上图虚线是真实分布，红线是通过 4 个高斯分布拟合出来的曲线，可以看出很接近真实分布
GMM 一般使用 EM 优化算法去估计参数的隐变量 Z

参考：