本文使用一个两层的神经网络,推导深度学习中经典的过程:链式求导
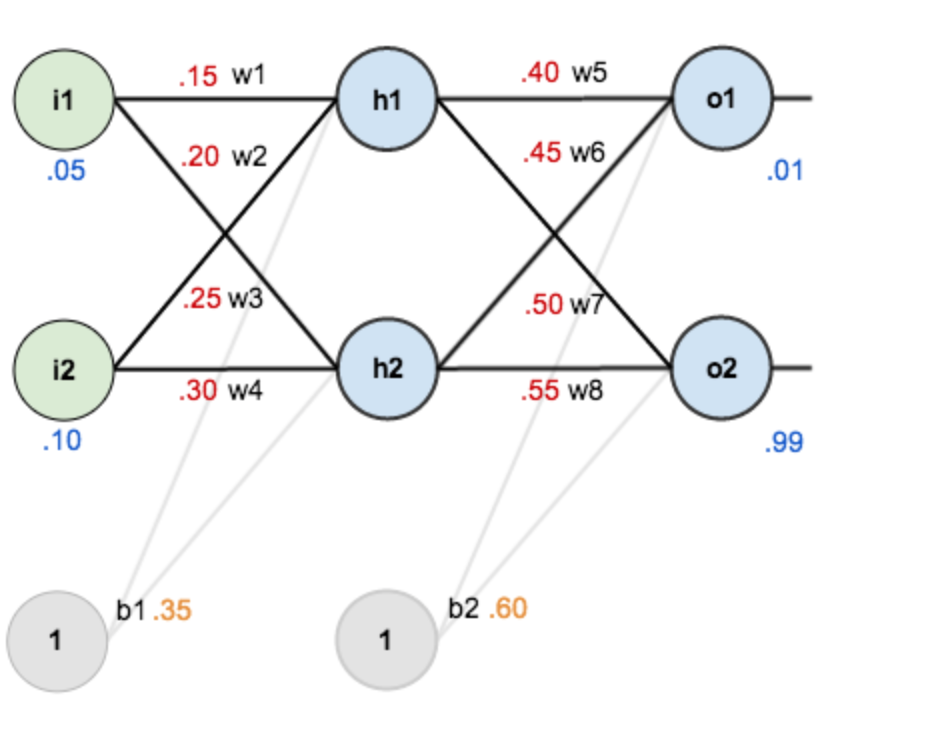
原始网络结构
![网络结构]()
链式求导法则,从网络的输出层将输入层逐层回传误差,并求得每个参数要下降的梯度。
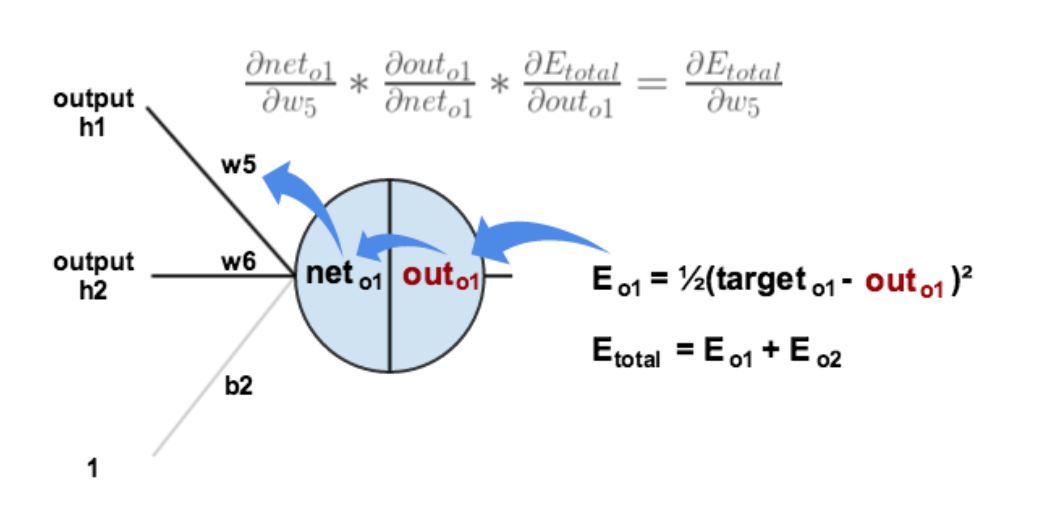
1. 输出层的前一层之间的参数更新
![倒数第二层参数更新示意图]()
对于一个神经元来说,其更新节点前的边权重过程需要求三个导数,分别是:
(1) 边上尾节点总的误差与输出之间的导数,即目标函数与输出之间的导数
Der1=σ(Outo1)σ(Etotal)=σ(Outo1)σ(Eo1+Eo2)=σ(Outo1)σ(21((trage1−Outo1)2+(trage2−Outo2)2)=Outo1−trage1
(2) 边上尾节点输出和其激活函数的导数
Der2=σ(neto1)σ(Outo1)=σ(neto1)σ(1+e−neto11)=outo1(1−outo1)
(3) 边上尾节点输入与该边的导数
Der3=σ(w5)σ(neto1)=σ(w5)σ(Outh1∗w5+b)=Outh1
边权重w5下降的梯度为以上三个导数的乘积。
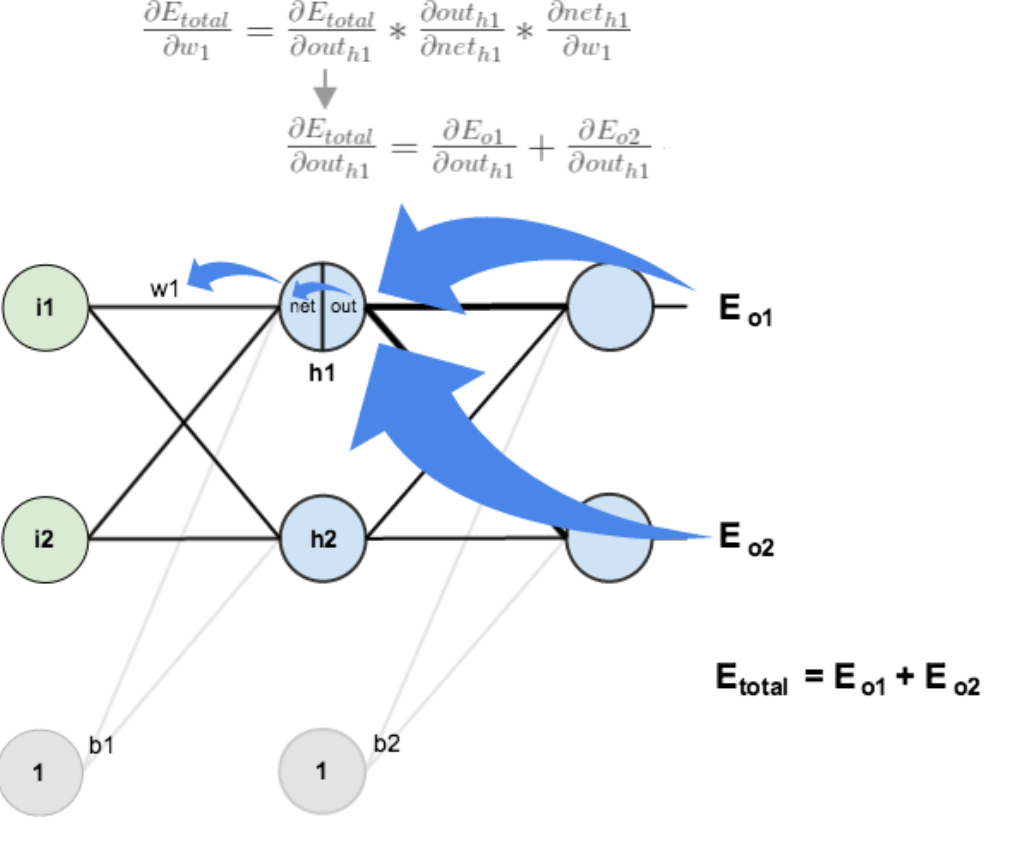
2. 其他层参数更新
![倒数第三层参数更新示意图]()
下面展示求目标函数对权重w1的梯度,
总体公式:
σ(w1)σ(Etotal)=σ(Outh1)σ(Etotal)∗σ(neth1)σ(Outh1)∗σ(w1)σ(neth1)
其中:
σ(Outh1)σ(Etotal)=σ(Outh1)σ(Eo1)+σ(Eo2)=σ(Outh1)σ(Eo1)+σ(Outh1)σ(Eo2)=σ(Outh1)σ(Eo1+Eo2)
σ(Outh1)σ(Eo1)=σ(neto1)σ(Eo1)∗σ(Outh1)σ(neto1)
σ(neto1)σ(Eo1)=σ(Outo1)σ(Eo1)∗σ(neto1)σ(Outo1)
通过以上公式可以计算出,目标函数对权重w1的梯度。
参考:
大白话讲解 BP 算法