损失函数 - 交差熵演进过程

发表于 2023-05-10 更新于 2025-02-07 分类于 2-深度学习， A-深度学习基础阅读次数：本文字数： 7.1k 阅读时长 ≈ 6 分钟

本脚本用于分析交叉熵的计算原理，主要分析从模型输出到交叉熵损失计算结果的过程

在 Pytorch 中，计算交差熵的过程如下：

import torch

torch.manual_seed(1)

dummy_input = torch.rand([3, 3])
dummy_target = torch.LongTensor([0, 1, 2])
print(dummy_input.shape,dummy_input)
print(dummy_target.shape,dummy_target)

certerion = torch.nn.CrossEntropyLoss(reduction='mean')
loss = certerion(dummy_input, dummy_target)
print(loss)

torch.Size([3, 3]) tensor([[0.7576, 0.2793, 0.4031],
		[0.7347, 0.0293, 0.7999],
		[0.3971, 0.7544, 0.5695]])
torch.Size([3]) tensor([0, 1, 2])
tensor(1.2005)

交叉熵的计算是基于 “熵” 的，熵在物理上是表示混乱程度、不确定性的度量，在信息论中表示对分布 “信息量” 期望，所以下面我们将按照 " 信息量 -> 熵 -> 交叉熵 " 的顺序讲解

信息量

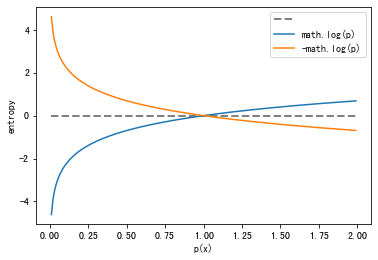
信息量表示概率空间中的单一事件或离散随机变量的值相关信息量的量度，如果一件事情的概率很低，那么它的信息量就很大；反之，如果一件事情的概率很高，它的信息量就很低。简而言之，概率小的事件信息量大。其计算公式如下：

H(x)=log{\frac {1} {p(x)}}=- log[p(x)]

，其中 $p(x)$ 表示事件发生的概率， $p(x) \in [0,1]$

# 熵和概率的关系
import matplotlib.pyplot as plt
import math
px = [i/100.0 for i in range(1, 200)]

plt.plot(px, [0 for p in px], color='gray',
         linewidth=2.0, linestyle='--')  # x轴
plt.plot(px, [math.log(p) for p in px])
plt.plot(px, [-math.log(p) for p in px])
plt.xlabel('p(x)')
plt.ylabel('entropy')
plt.legend(["", "math.log(p)", "-math.log(p)"], loc='upper right')
plt.show()

png

例子： 在一次国际象棋比赛中张三获得冠军的可能性为 0.1（记为事件 A），而在另一次国际象棋比赛中她得到冠军的可能性为 0.9（记为事件 B）。试分别计算当你得知她获得该次比赛冠军时，从中获得的信息量各为多少？

\begin{aligned} &\mathrm{H}(\mathrm{A})=-\log _{2} p(0.1) \approx 3.32 \\ &\mathrm{H}(\mathrm{B})=-\log _{2} p(0.9) \approx 0.152 \end{aligned}

熵

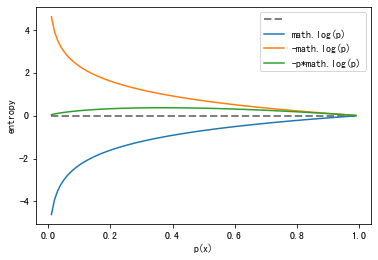
熵在物理上是表示混乱程度、不确定性的度量，在信息论中表示对分布 “信息量” 期望，已知期望是概率与值的乘积，所以熵计算公式如下：

H(p)=-\sum_xp(x)log(p(x))

， $p(x) in [0,1]$ 为概率，可知 p (i)=0 或 p (i)=1 时，事件已经确定，熵最小；p (i)=0.5 时，事件不确定性最大，熵最大

# 熵和概率的关系
import matplotlib.pyplot as plt
import math
px = [i/100.0 for i in range(1, 100)]

plt.plot(px, [0 for p in px], color='gray',
         linewidth=2.0, linestyle='--')  # x轴
plt.plot(px, [math.log(p) for p in px])
plt.plot(px, [-math.log(p) for p in px])
plt.plot(px, [-p*math.log(p) for p in px])
plt.xlabel('p(x)')
plt.ylabel('entropy')
plt.legend(["", "math.log(p)", "-math.log(p)",
           '-p*math.log(p)'], loc='upper right')
plt.show()

png

交叉熵

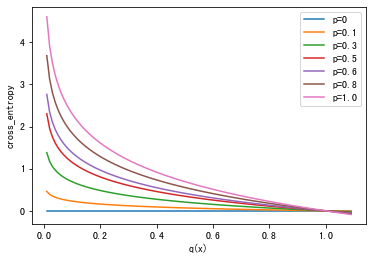
交叉熵表示实际输出（概率）与期望输出（概率）分布的距离，也就是交叉熵的值越小，两个概率分布就越接近

# 交叉熵不同P值的变化的关系
import matplotlib.pyplot as plt
import math
p=[0,0.1,0.3,0.5,0.6,0.8,1.0]
q = [i/100.0 for i in range(1, 110,1)]

lines=[]
titles=[]
for i in range(len(p)):
    p_=p[i]
    plt.plot(q, [-p_*math.log(q_) for q_ in q])
    titles.append(F'p={p_}')

plt.xlabel('q(x)')
plt.ylabel('cross_entropy')
plt.legend(titles, loc='upper right')
plt.show()

png

现有模型输出 p=[0.5,0.2,0.3]，期望输出 q1=[1,0,0], 则其交叉熵损失应该如何计算？比较模型输出 q2=[0.8,0.1,0.1] 的交叉熵损失？

对应 p 和 q1, 整理得到以下数据

含义	值	备注
q1	[1,0,0]	期望输出
p	[0.5,0.2,0.3]	模型对 1 的预测

按照熵的计算公式，得到以下：

\begin{array}{l} \left.H\left(p, q_{1}\right)=-(1 \log 0.5+0 \log 0.2+0 \log 0.3\right)=0.6931 \\ \left.H\left(p, q_{2}\right)=-(1 \log 0.8+0 \log 0.1+0 \log 0.1\right)=0.2231 \end{array}

其中 q2 比 q1 的预测更准确，其熵更低

可以发现，计算交叉熵时，要求模型输出按 [0,1] 的概率输出，且各个类别加起来等于 1，所以经常在模型输出后使用 softmax 函数对输出进行处理。softmax 的计算公式为：

\sigma(z)_j = \frac{p}{\sum_{k=1}^K p^{k}}

, 其中 p 为某个类别的输出值，K 表示类别数量。以上例子 softmax 后的概率是 [0.5,0.2,0.3],[0.8,0.1,0.1]，通过以上公式反向计算模型输出为 [0.7467,-0.1696,0.2359],[1.2666,-0.8129,-0.8129]，调用 Pytorch 的交叉熵函数计算损失为 [0.6931, 0.2231]

import torch

# 由概率逆向计算模型输出
dummy_input = torch.FloatTensor([[0.5, 0.2, 0.3], [0.8, 0.1, 0.1]])
model_output = torch.sum(torch.exp(dummy_input),
                         dim=1).view(-1, 1).expand_as(dummy_input)
print(model_output)  # 逆softmax过程

model_output = torch.log(model_output*dummy_input)
print(model_output)  # 模型输出
probs = torch.nn.functional.softmax(model_output, dim=1)
print(probs)  # 对模型输出求softmax，可以看出与dummy_input相等

# 调用Pytorch的CrossEntropyLoss计算损失
dummy_target = torch.LongTensor([0, 0])
certerion = torch.nn.CrossEntropyLoss(reduction='none')
loss = certerion(model_output, dummy_target)
print(loss)

tensor([[4.2200, 4.2200, 4.2200],
		[4.4359, 4.4359, 4.4359]])
tensor([[ 0.7467, -0.1696,  0.2359],
		[ 1.2666, -0.8129, -0.8129]])
tensor([[0.5000, 0.2000, 0.3000],
		[0.8000, 0.1000, 0.1000]])
tensor([0.6931, 0.2231])

实际上，Pytorch 的 CrossEntropyLoss 包含以下 3 个过程：

softmax 过程：得到每个类别的预测结果
log 过程：求取各个类别的熵
nlll 过程：取出对应类别的熵，并做平均

# 模型输出计算softmax，此时可以看到每一行加到一起结果都是1
softmax_func = torch.nn.Softmax(dim=1)
soft_output = softmax_func(model_output)
print(soft_output)

# 在softmax的基础上取log
log_output = torch.log(soft_output)
print(log_output)

# 对比softmax与log的结合与nn.LogSoftmaxloss(负对数似然损失)的输出结果，发现两者是一致的。
logsoftmax_func = torch.nn.LogSoftmax(dim=1)
logsoftmax_output = logsoftmax_func(model_output)
print(logsoftmax_output)

# pytorch中关于NLLLoss的默认参数配置为：reducetion=True、size_average=True
nllloss_func = torch.nn.NLLLoss(reduction='none')
nlloss_output = nllloss_func(logsoftmax_output, dummy_target)
print(nlloss_output)

tensor([[0.5000, 0.2000, 0.3000],
		[0.8000, 0.1000, 0.1000]])
tensor([[-0.6931, -1.6094, -1.2040],
		[-0.2231, -2.3026, -2.3026]])
tensor([[-0.6931, -1.6094, -1.2040],
		[-0.2231, -2.3026, -2.3026]])
tensor([0.6931, 0.2231])

torch.nn.NLLLoss 的作用：取出对应位置的值并乘上 - 1，如果 reduction=‘mean’, 则对所有位置求均值

# 举例
dummy_input = torch.arange(0, 9, 1).view([3, 3])/10
dummy_target = torch.LongTensor([0, 1, 2])
print(dummy_input, dummy_target)

nllloss_func = torch.nn.NLLLoss(reduction='none')
nlloss_output = nllloss_func(dummy_input, dummy_target)
print(nlloss_output)

tensor([[0.0000, 0.1000, 0.2000],
		[0.3000, 0.4000, 0.5000],
		[0.6000, 0.7000, 0.8000]]) tensor([0, 1, 2])
tensor([-0.0000, -0.4000, -0.8000])

二分类的交叉熵

在深度学习的分类任务中，常常还遇到多标签的情况，这时候激活函数由 softmax 变为 sigmoid，损失函数变为 torch.nn.BCELoss, 注意：此时的标签要变为 one-hot 模式

import torch

torch.manual_seed(1)

dummy_input = torch.Tensor([[0.4, 0.3, 0.2]])
dummy_target = torch.FloatTensor([[1, 0, 1]])
print(dummy_input)
print(dummy_target)

certerion = torch.nn.BCELoss(reduction='none')
loss = certerion(dummy_input, dummy_target)
print(loss)

1
2
3

tensor([[0.4000, 0.3000, 0.2000]])
tensor([[1., 0., 1.]])
tensor([[0.9163, 0.3567, 1.6094]])

现有模型输出 p=[0.4,0.3,0.2]，期望输出 q1=[1,0,1], 则其交叉熵损失应该如何计算？比较模型输出 q2=[0.8,0.1,0.9] 的交叉熵损失？

含义	值	备注
q1	[1,0,1]	期望输出
p	[0.4,0.3,0.2]	模型对 1 的预测
p	[0.6,0.7,0.8]	模型对 1 的预测

由于存在 “多标签”，所以每个标签都需要学习，即都学习计算损失

\begin{array}{l} \left.H\left(p, q_{1}\right)=-(1 \log 0.4+ (1-0)\log (1-0.3)+1 \log 0.2\right)=2.8824 \\ \left.H\left(p, q_{2}\right)=-(1 \log 0.8+ (1-0)\log (1-0.9)+1 \log 0.9\right)=0.4338 \end{array}

可以看出，q2 更接近期望输出，所以其损失更小

总结：

计算熵表示变量的混乱程度，通过交叉熵评估模型输出和真实数据之间的不匹配程度，然后神经网络通过参数更新，减小这种不匹配程度，达到数据学习的目的。其本质就是 “熵减” 的过程
对于一个样本而言，如果其只是单标签分类，交叉熵只关注其真实类别对应的熵，而不关注其他类别对应的熵，这点从 torch.nn.NLLLoss 取值体现出来；如果是多标签分类，由于每个类别都需要被监督，因此需要计算所有类别的损失
CE 主要用于多分类，也可用于二分类，用于二分类时输出 2 个特征
BCE 用于二分类，输出 1 个特征即可
CE 搭配 softmax 使用，BCE 搭配 sigmoid 使用，Pytorch 的 CE 自带 softmax 过程，BCE 没有自带 sigmoid，但是 BCEWithLogic 是自带的