深度学习的损失函数

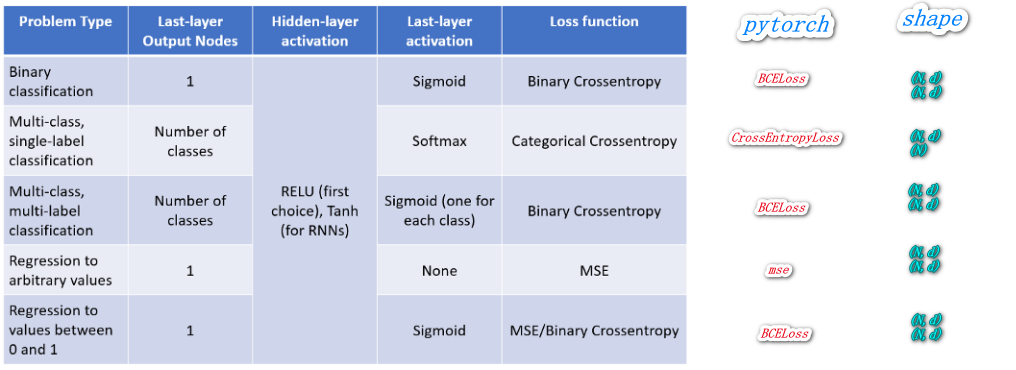
发表于 2023-10-30 分类于 2-深度学习， A-基础知识阅读次数：本文字数： 28k 阅读时长 ≈ 25 分钟

本文讲解神经网络使用的损失，用于衡量模型输出与标签值的差异，尤其需要把握的是不同模型输出使用不同的激活函数，然后使用不同损失函数去计算

什么是损失函数？

损失函数是用来度量模型预测值和真实值间的偏差，偏差越小，模型越好，所以我们需要最小化损失函数
神经网络的学习过程就是不断减小模型损失的过程，这个过程设计 2 个步骤：1）计算损失函数；2）通过优化函数修改参数以减小损失值
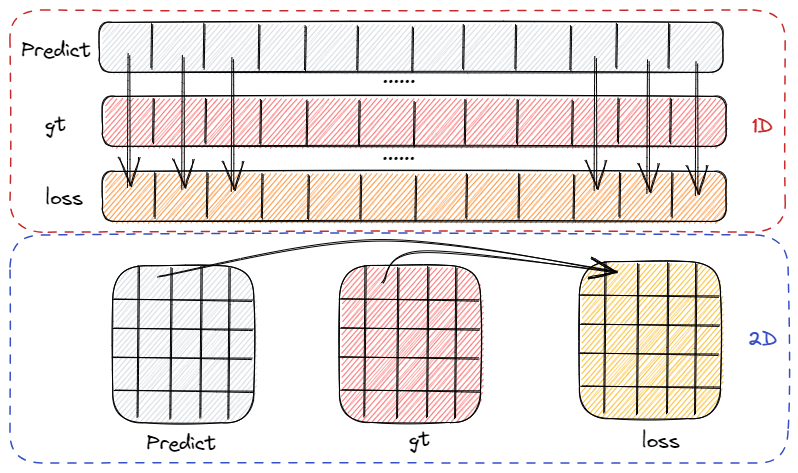
计算损失值的过程是针对每个预测点位计算损失，如图是 1D、2D 场景下的损失计算示意图，每个点位都有对应损失。计算过程可以是只有对应位置参加，如 MSE，交叉熵，也可以是全局点位参加，如 Dice loss

损失函数和目标函数的区别？

损失函数(代价函数)： 损失函数越小，就代表模型拟合的越好
目标函数： 把要最大化或者最小化的函数（模型迭代时的迭代方向，往目标函数最小化的方向迭代）称为目标函数，有正则化 (regularization) 的必定是目标函数

什么是绝对值损失(L1Loss)？

等价于 L1损失，相当于在做中值回归，相比做均值回归的平方损失函数，绝对损失函数对异常点更鲁棒 $L(Y, f(x)) = |Y-f(x)|$

什么是平方损失(MSELoss/L2Loss)?

等价于 L2损失，是光滑函数，能够使用梯度下降法优化。然而当预测值距离 gt 是只越远时，平方损失函数的惩罚力度越大，因此对异常点比较敏感 $L(Y, f(x)) =\frac {1} {2} \sum_N{(Y-f(x))}^2$

平方损失 (MSELoss/L2Loss) 的梯度分析？

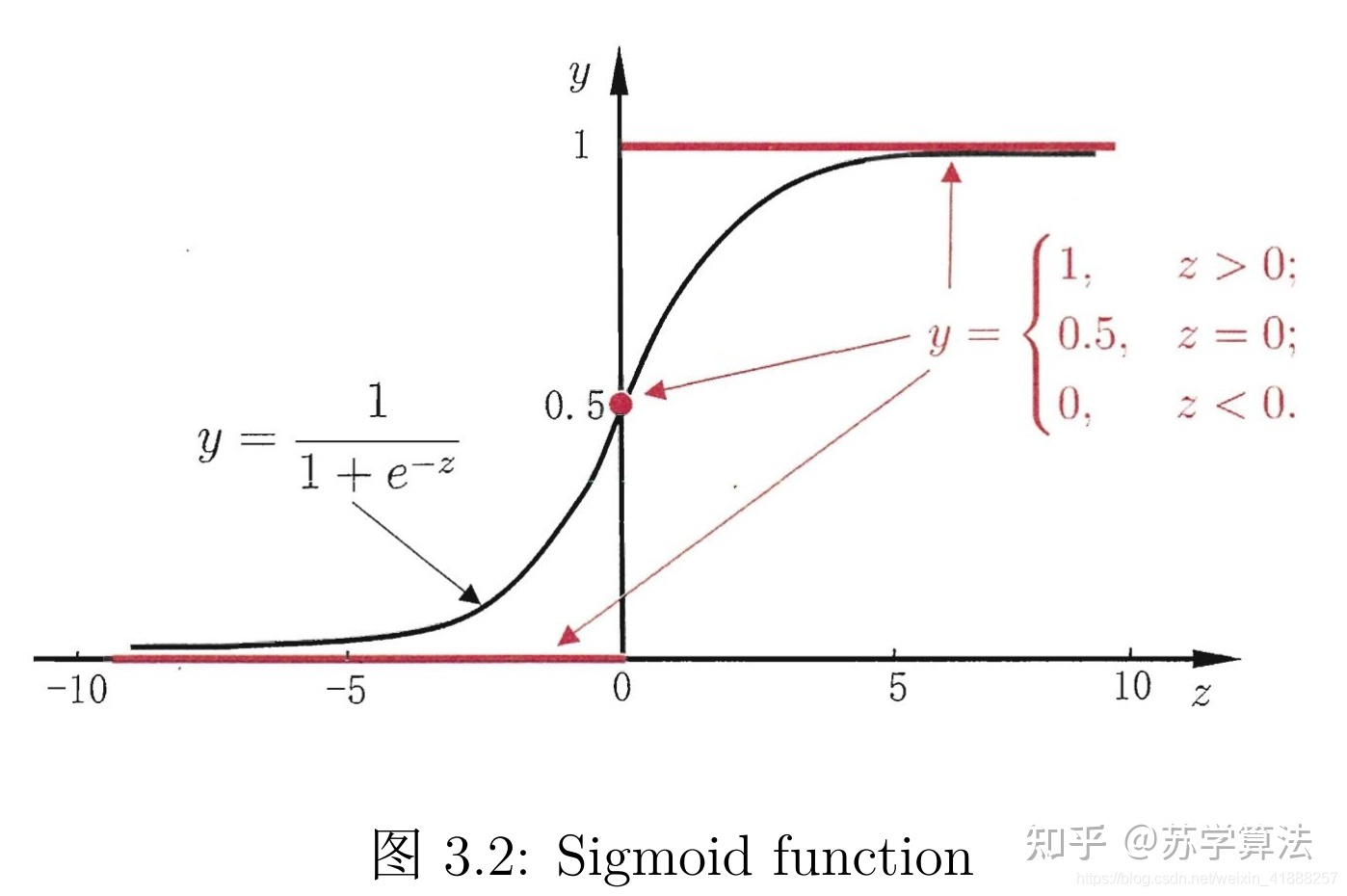
以下公式 y 是期望输出，Y 是实际输出，z=wx+b，Y=sigmoid (z)，已知 Y 关于 z 的梯度是 Y (1-Y)，则 MSE 梯度为
$\begin{aligned}\frac{\partial C}{\partial w} =\frac{\partial C}{\partial z}\frac{\partial z}{\partial w}=(Y-y)x\sigma'(z)=(Y-y)Y(1-Y)x\approx Y\sigma'(z)\\ \frac{\partial C}{\partial b} =(Y-y)\sigma'(z)=(Y-y)Y(1-Y)\approx Y\sigma'(z)\end{aligned}$
网络更新慢：因为 sigmoid 函数的性质，如图的两端，几近于平坦，导致\sigma’ (z)在 z 取大部分值时会很小，这样会使得 w 和 b 更新非常慢
无法区分小梯度：y=1, Y=0 、y=1, Y=1、y=0, Y=1、y=0, Y=0 的梯度一样，都是 0，当梯度很小的时候，MSE无法知道是离目标很远还是已经在目标附近了。（离目标很近和离目标很远，其梯度都很小）

什么是平滑绝对值损失(SmoothL1Loss)?

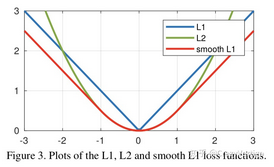
又称Huber Loss，在Fast RCNN提出的损失函数，是在结合绝对值损失(L1Loss) 、平方损失(MSELoss/L2Loss)的基础上提出的
$L(Y,f(x))= \begin{cases}0.5 [Y-f(x)]^{2} & |Y-f(x)|<1 \\ |Y-f(x)|-0.5 & \text { otherwise }\end{cases}$
一阶导数：
$\frac{d s m o o t h L 1_{1}(x)}{x}=\left\{\begin{array}{rr} f(x) & \text { if }|f(x)|<1 \\ \pm 1 & \text { otherswise } \end{array}\right.$
L1损失函数为常数，在训练后期，Y与f(x)很小时，如果学习速率 (learning rate) 不变，损失函数会在稳定值附近波动，很难收敛到更高的精度；L2损失函数对x的导数在x值很大时，其导数也非常大，在训练初期不稳定。 Smooth L1 Loss完美避开了L1、L2损失的缺点

什么是交叉熵损失 (CE Loss) ?

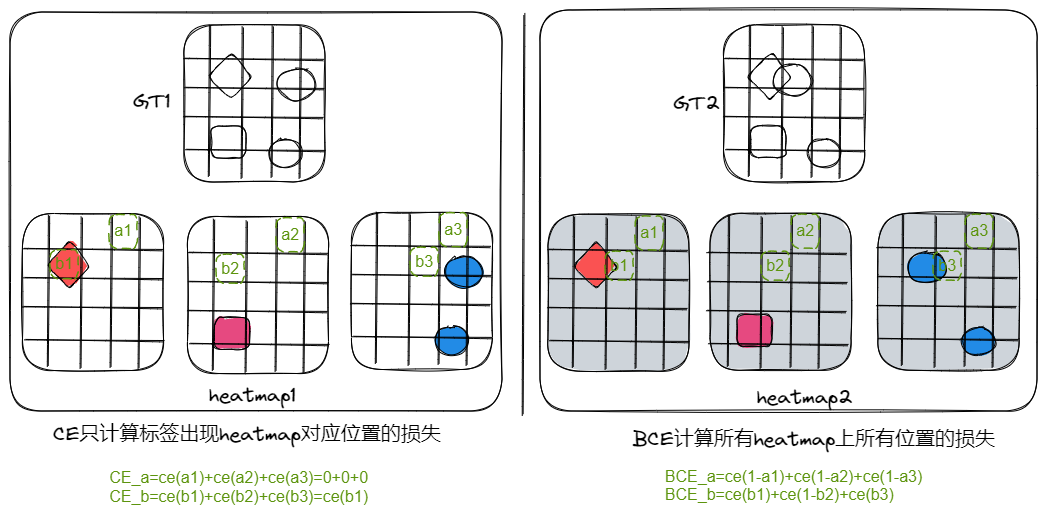
交叉熵(CrossEntropy) 就是交差熵损失，该值表示实际输出（概率）与期望输出（概率）分布的距离，也就是交叉熵的值越小，两个概率分布就越接近
二分类 (BCE)： $y_i$ 表示样本 i 的标签，正类为1，负类为0； $p_i$ 为样本 i 为正类的概率
$L=\frac{1}{N} \sum_{i} L_{i}=\frac{1}{N} \sum_{i}-\left[y_{i} \cdot \log \left(p_{i}\right)+\left(1-y_{i}\right) \cdot \log \left(1-p_{i}\right)\right]$
多分类 (CE)： $M$ 为类别数量； $y_i$ 表示样本 i 的标签， $p_{ic}$ 为样本 i 为 c 的概率
$L=\frac{1}{N} \sum_{i} L_{i}=-\frac{1}{N} \sum_{i} \sum_{c=1}^{M} y_{i c} \log \left(p_{i c}\right)$
在区分前景、背景的二分类时，当前景像素的数量远远小于背景像素的数量时，y=0的数量远大于y=1的数量，损失函数y=0的成分就会占据主导，使得模型严重偏向背景，导致效果不好

在多分类任务中，交叉熵擅长于学习类间的信息，因为它采用了类间竞争机制，它只关心对于正确标签预测概率的准确性，忽略了其他非正确标签的差异，导致学习到的特征比较散

>>> dummy_input=torch.rand([1,10,3,3])
>>> dummy_target = torch.randint(0,11,[1,3,3]) #为每个位置生成一个gt标签                                                                    
>>> dummy_input.shape,dummy_target.shape
(torch.Size([1, 10, 3, 3]), torch.Size([1, 3, 3]))
>>> dummy_target
tensor([[[ 8,  9,  1],  
        [ 4,  0,  6],  
        [10,  0,  1]]])
>>> certerion = torch.nn.CrossEntropyLoss(reduction='none',ignore_index=10)
>>> certerion(dummy_input,dummy_target) # 忽略类别损失为0
tensor([[[1.9907, 2.7757, 2.2835],
        [2.7387, 2.1581, 2.3648],
        [0.0000, 2.4749, 2.0570]]])

什么是二值交叉熵损失(BCELoss)？

二值交叉熵损失 (Binary Cross Entropy Loss，BCELoss)，用于二分类，不能进行多分类，但是可进行多标签分类（一个样本对应多个标签）

BCEWithLogitsLoss 将 sigmoid 和二值交叉熵损失 BCELoss 合并为一步，以下3种方式计算结果相同

>>> dummy_input=torch.rand([1,10,3,3])
>>> dummy_target = torch.randint(0,10,[1,10,3,3],dtype=torch.float32) #为每个位置生成多个gt标签 
>>> dummy_input.shape,dummy_target.shape # shape必须一致
(torch.Size([1, 10, 3, 3]), torch.Size([1, 10, 3, 3]))   
>>> crition1 = torch.nn.BCEWithLogitsLoss()
>>> crition1(dummy_input,dummy_target)      
tensor(-1.2125)
>>> crition2 = torch.nn.MultiLabelSoftMarginLoss()
>>> crition2(dummy_input,dummy_target)
tensor(-1.2125)
>>> crition3 = torch.nn.BCELoss()
>>> crition3(torch.sigmoid(dummy_input), dummy_target) 
tensor(-1.2125)

什么是 KL 散度损失 (KLDivLoss)？

KL散度衡量两个连续分布之间的距离。两个分布越相似，KL散度越接近0，KL散度又称相对熵
$\operatorname{los} s(x, y)=\frac{1}{n} \Sigma_{i}\left(x_{i} \times \log \frac{x_{i}}{y_{i}}\right)$
注意，使用nn.KLDivLoss计算KL(pred|target)时，需要将pred和target调换位置，而且target需要先取对数
在机器学习的分类问题中，我们希望缩小模型预测和标签之间的差距，即 KL 散度越小越好，在这里由于 KL 散度中的 H (p)项不变（在其他问题中未必），故在优化过程中只需要关注交叉熵就可以了，因此一般使用交叉熵作为损失函数

交叉熵损失 (CE Loss) 的梯度分析？

对于交叉熵损失而言，每个位置都有损失，那么每个位置都有梯度，下面展示如何求一个位置的梯度。值得注意的是，对于多类别的分割来说，有类别对应的 heatmap 计算损失并且有梯度，非类别的其他 heatmap 不计算损失但是有梯度
前向计算：计算模型输出是 $z_j$ ，经过 softmax 函数后得到输出概率值，已知 softmax 的计算公式及其导数如下
$\begin{array}{l}f(a_k^L)=\dfrac{e^{z_k^L}}{\sum\limits_{j=1}^N e^{z_j^L}}\\ \dfrac{\partial f(a_k^L)}{\partial a_j} =\dfrac{e^{a_i}\sum-e^{a_j}e^{a_i}}{\sum^2}\end{array}$
计算损失：利用交叉熵计算损失，其中 $a_j$ 是类别 j 的输出概率，N 表示类别数量， $y_i$ 是 gt 值，如果当前点位的类别是 k，则有 $y_k=1$ ，那么这个点位的损失计算如下：
$J=-\sum\limits_{j=1}^N y_j\log a_j^L=-\log a_k^L$
反向传播：反向传播需要对每个 $z_j^L$ 求导数，此时分为两种情况，j=k 和 j!=k，意思是将有类别对应的位置和无类别对应位置的梯度分开处理
J=k 时，激活值使用 softmax 输出，并且计算损失，梯度为：
$\begin{array}{ll}\dfrac{\partial J}{\partial z_j^2}=\dfrac{\partial J}{\partial z_k^2}&=\dfrac{\partial J}{\partial a_k^2}\dfrac{\partial a_k^L}{\partial z_k^2}\\ &=-\dfrac{1}{a_k^2}\dfrac{\left(e^{i\frac{1}{k}}\right)\sum_{j=1}^{N}e^{i\frac{1}{j}}-e^{i\frac{1}{k}}e^{i\frac{1}{k}}}{\left(\sum_{j=1}^{N}e^{i\frac{1}{j}}\right)^2}\\ &=-\dfrac{1}{a_k^2}a_k^{\frac{1}{k}}\left(1-a_k^{\frac{1}{k}}\right)\\ &=a_k-1\end{array}$
J!=k 时，激活值使用 softmax 输出，不计算损失，梯度为：
$\begin{aligned}\frac{\partial J}{\partial z_j^L}&=\frac{\partial J}{\partial a_k^L}\frac{\partial a_k^L}{\partial z_j^L}\\ \\ &=-\frac{1}{a_k^L}\frac{0*\sum\limits_{j=1}^N e^{z_j^L}-e^{z_k^L}e^{z_j^L}}{(\sum\limits_{j=1}^Ne^{z_j^L})^2}\\ \\ &=a_j^L\end{aligned}$
合并以上两个式子，得到以下公式，也就是某个点位上关于某个类别的梯度，等于其激活值减对应 gt 值
$\dfrac{\partial J}{\partial z_j^L}=a_j^L-y_j$

注意：虽然交叉熵不计算背景点位的损失，但是求损失对权重梯度时，背景部分有共享梯度，这是因为根据链式求导损失->激活->输出 (权重计算得到)时，激活函数在背景上有梯度回传

>>> input=torch.tensor([[-0.3589,  0.6440],[ 0.7927, -0.0011]], dtype=torch.float, requires_grad=True)
>>> target=torch.LongTensor([0,1])
>>> loss=torch.nn.CrossEntropyLoss(reduction='mean')
>>> output=loss(input,target)
>>> output
tensor(1.2411, grad_fn=<NllLossBackward0>)
>>> output.backward()
>>> input.grad
tensor([[-0.3658,  0.3658], 
        [ 0.3443, -0.3443]])
>>> m=torch.nn.Softmax(dim=1) 
>>> prob=m(input)
>>> prob
tensor([[0.2684, 0.7316],
        [0.6886, 0.3114]], grad_fn=<SoftmaxBackward0>)
# 确实是prob-target为回传梯度，其中[[1,0],[0,1]]为target的one-hot化
# 并且可以发现背景虽然不计算损失，但是也在回传梯度
>>> (prob-torch.from_numpy(np.array([[1,0],[0,1]])))/2 
tensor([[-0.3658,  0.3658],
        [ 0.3443, -0.3443]], grad_fn=<DivBackward0>)

二值化交叉熵损失 (BCELoss) 的梯度分析？

上图是模型输出概率分布及 ce loss 的梯度，假设 $a^L$ 是模型输出，y 是 gt 值，其损失及损失对模型输出的梯度为
$\begin{aligned}L &=-(y\log a^L+(1-y)\log(1-a^L)) \\ \frac{\partial J}{\partial z^L}&=\frac{\partial J}{\partial a^L}\partial a^L\\ &=(-\frac{y}{a^2}+\frac{1-y}{1-a^2}a^L(1-a^L)\\ &=-y(1-a^2)+(1-y)a^L\\ &=a^L-y\end{aligned}$
背景有梯度：由图可知，ce loss 下背景位置也有梯度累积，尤其是在训练前期，背景梯度占据主导地位
正负样本平等：同样的预测概率，ce loss 正负样本贡献的梯度一样

交叉熵损失 (CELoss) 、二值化交叉熵损失 (BCELoss) 对权重的梯度分析？

输入 (x)+权重 (w)=输出（z），以上已经分析得出两个损失函数对模型输出的梯度为
$\begin{array}{rcl}\frac{\partial J}{\partial z}= &=&a-y\end{array}$
后续针对输出+权重的计算方式求得损失对权重的梯度，已知 z=wx+b，那么
$\begin{aligned}\frac{\partial C}{\partial w_j}=\frac{1}{N}\sum_{i=1}^N(\sigma(z)-y)x_j=\frac{1}{N}\sum_{i=1}^N(a-y)x_j\\ \\ \frac{\partial C}{\partial b}=\frac{1}{N}\sum_{i=1}^N(\sigma(z)-y)=\frac{1}{N}\sum_{i=1}^N(a-y)\end{aligned}$
注意：虽然交叉熵不计算背景点位的损失，但是求损失对权重梯度时，背景部分有共享梯度，这是因为根据链式求导损失->激活->输出 (权重计算得到)时，激活函数在背景上有梯度回传

交叉熵 (CE) 与均方误差（MSE）的区别？

均方误差（MSE）的梯度：已知 MSE 的计算方式是 $C=(y-a)^2/2$ ，其中 y 是期望输出，a 是实际输出，z=wx+b，a=sigmoid (z)，则梯度为
$\begin{aligned}\frac{\partial C}{\partial w}=(a-y)\sigma'(z)x=(a-y)a(1-a)x\approx a\sigma'(z)\\ \frac{\partial C}{\partial b}=(a-y)\sigma'(z)=(a-y)a(1-a)\approx a\sigma'(z)\end{aligned}$
交叉熵 (CE)的梯度：还是使用 sigmoid 输出，然后使用 BCE 计算损失，其梯度如下
$\begin{aligned}\frac{\partial C}{\partial w_j}=\frac{1}{N}\sum_{i=1}^N(\sigma(z)-y)x_j=\frac{1}{N}\sum_{i=1}^N(a-y)x_j\\ \\ \frac{\partial C}{\partial b}=\frac{1}{N}\sum_{i=1}^N(\sigma(z)-y)=\frac{1}{N}\sum_{i=1}^N(a-y)\end{aligned}$
可知，对于 MSE，由于 $\sigma'(z)$ 在大部分区域内取趋向 0 的值，导致梯度较小，网络更新慢；CE 的w 的梯度公式中原来的 $\sigma'(z)$ 被消掉了，权重的更新是受（a-y）这一项影响（表示真实值和输出值之间的误差），即受误差的影响，所以当误差大的时候，权重更新就快，当误差小的时候，权重的更新就慢

神经网络输出激活函数与损失的搭配使用？

交叉熵损失(CrossEntropyLoss)：内部将input做了softmax后再与label进行交叉熵，网络输出搭配torch.nn.Linear(previous_layer_output_num, num_classes)
二值交叉熵损失BCELoss：内部啥也没干，直接将input与label做了交叉熵，网络输出搭配torch.sigmoid
BCEWithLogitsLoss：内部将input做了sigmoid后再与label进行交叉熵，网络输出torch.nn.Linear(previous_layer_output_num, num_classes)

当我们有 C 个目标需要分割时，模型应该如何输出 C 个类别预测还是 C+1 个？

交差熵指出当模型输出是 C 个类别时，目标 (gt)上的值必须是[0, C)之间的，但是由于要考虑背景输出，所以目标 (gt)一定有 C+1 个类别，所以模型输出必须是 C+1

>>> pre=torch.rand(2,4,3,3) # 假设输出是4个类别
>>> target=torch.randint(0,5,(2,3,3),dtype=torch.long) 
>>> crit=torch.nn.CrossEntropyLoss(reduction='none')
>>> crit(pre,target)                                    
Traceback (most recent call last):
IndexError: Target 4 is out of bounds. # 报错，因为gt上的值超过4
>>> target=torch.randint(0,4,(2,3,3),dtype=torch.long)  
>>> crit(pre,target)
tensor([[[1.2303, 1.0533, 1.5691],
        [1.9121, 1.5518, 1.2985],
        [1.6926, 1.4423, 1.7514]],
        [[1.7121, 1.8669, 1.1509],
        [1.6110, 1.5210, 1.0275],
        [1.1983, 1.1457, 1.0641]]])

什么是Dice loss?

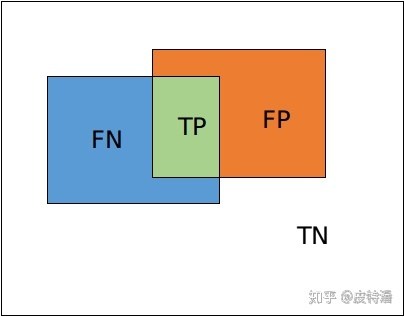
dice loss 来自 dice-coefficient，dice-coefficient 是一种评估两个样本相似性的度量函数，取值范围在0到1之间，取值越大表示越相似。dice loss 是一种区域相关的 loss。意味着某像素点的 loss 以及梯度值不仅和该点的 label 以及预测值相关，和其他点的 label 以及预测值也相关 (看分母)，这点和 ce loss (交叉熵)不同，定义如下： $$DiceLoss=1-dice=1- \frac{2|X \cap Y|}{|X|+|Y|}=1-\frac{2 TP}{2 TP+FP+FN}=1-F1score$$ |X|和|Y|分别表示 X 和 Y 的元素个数. 其中分子中的系数2，是因为分母存在重复计算 X 和 Y 之间的共同元素的原因。并且 dice coefficient 是等同 F1 score，优化 dice 等同于优化 F1 score
$|\mathrm{X} \cap \mathrm{Y}|=\left[\begin{array}{llll}0.01 & 0.03 & 0.01 & 0.03 \\0.02 & 0.02 & 0.02 & 0.02 \\0.85 & 0.85 & 0.86 & 0.86 \\0.95 & 0.95 & 0.96 & 0.96\end{array}\right] *\left[\begin{array}{cccc}0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\1 & 1 & 1 & 1 \\1 & 1 & 1 & 1\end{array}\right] \Rightarrow\left[\begin{array}{cccc}0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\0.85 & 0.85 & 0.86 & 0.86 \\0.95 & 0.95 & 0.96 & 0.96\end{array}\right] =7.24$

Dice loss 对正负样本严重不平衡的场景有着不错的性能，训练过程中更侧重对前景区域的挖掘。但训练 loss 容易不稳定，尤其是小目标的情况下。另外极端情况会导致梯度饱和现象。因此有一些改进操作，主要是结合 ce loss 等改进，比如: dice+ce loss，dice + focal loss 等

class DiceLoss(nn.Module):
 def __init__(self, weight=None, size_average=True):
     super(DiceLoss, self).__init__()
 def forward(self, inputs, targets, smooth=1):
     #comment out if your model contains a sigmoid or equivalent activation layer
     inputs = F.sigmoid(inputs)       
     #flatten label and prediction tensors
     inputs = inputs.view(-1)
     targets = targets.view(-1)
     intersection = (inputs * targets).sum()                            
     dice = (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth)  
     return 1 - dice

dice loss 的梯度分析？

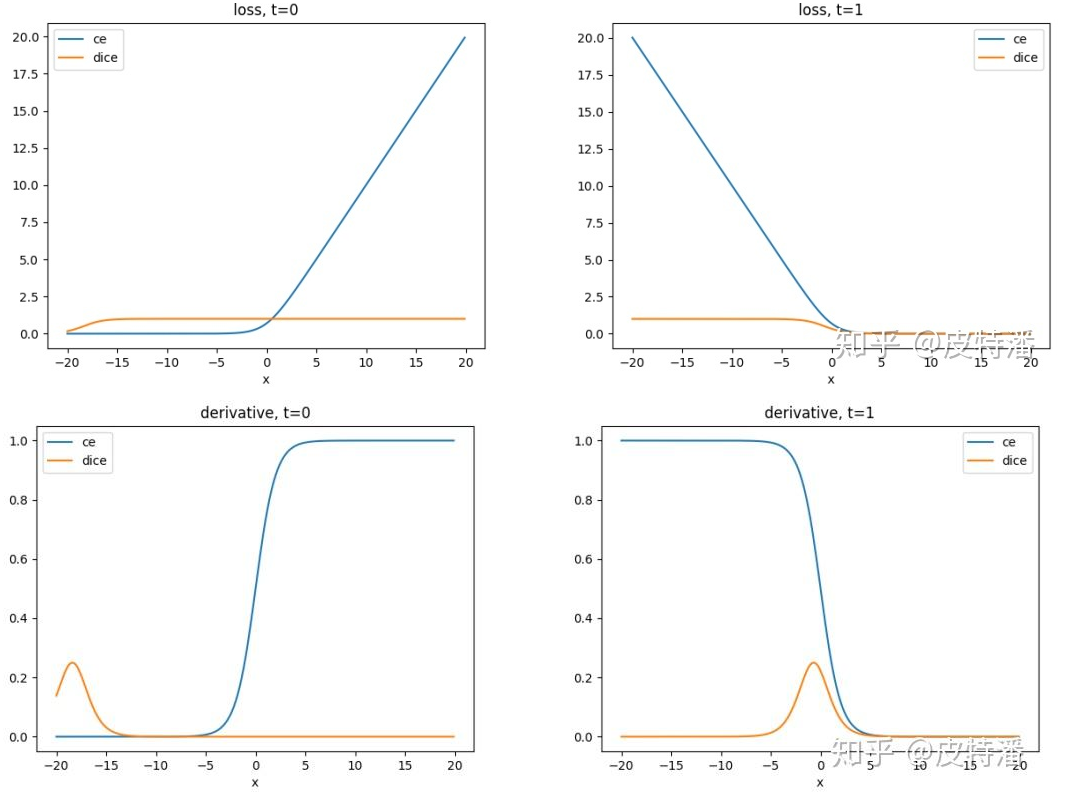
计算输出：假设只考虑 sigmoid 输出的二分类问题，求某一点的损失函公式如下，其中 t 是 gt，y=sigmoid (x) ，
$L_{dice}=1-\frac{2ty+\varepsilon}{t+y+\varepsilon}=\begin{cases}\frac{y}{y+\varepsilon}&\text{t=0}\\ \frac{1-y}{1+y+\varepsilon}&\text{t=1}\end{cases}$
计算梯度：
$\begin{aligned}{l}\frac{dL_{dice}}{dy}&=-\frac{2t\left(t+y+\varepsilon\right)-2ty-\varepsilon}{\left(t+y+\varepsilon\right)^2}=\begin{cases}\frac{\varepsilon}{\left(y+\varepsilon\right)^2}&\text{t=0}\\ -\frac{2+\varepsilon}{\left(1+y+\varepsilon\right)^2}&\text{t=1} \end{cases} \\ \frac{dL_{dice}}{dx}&=\frac{dL_{dice}}{dy}\frac{dy}{dx}\end{aligned}$
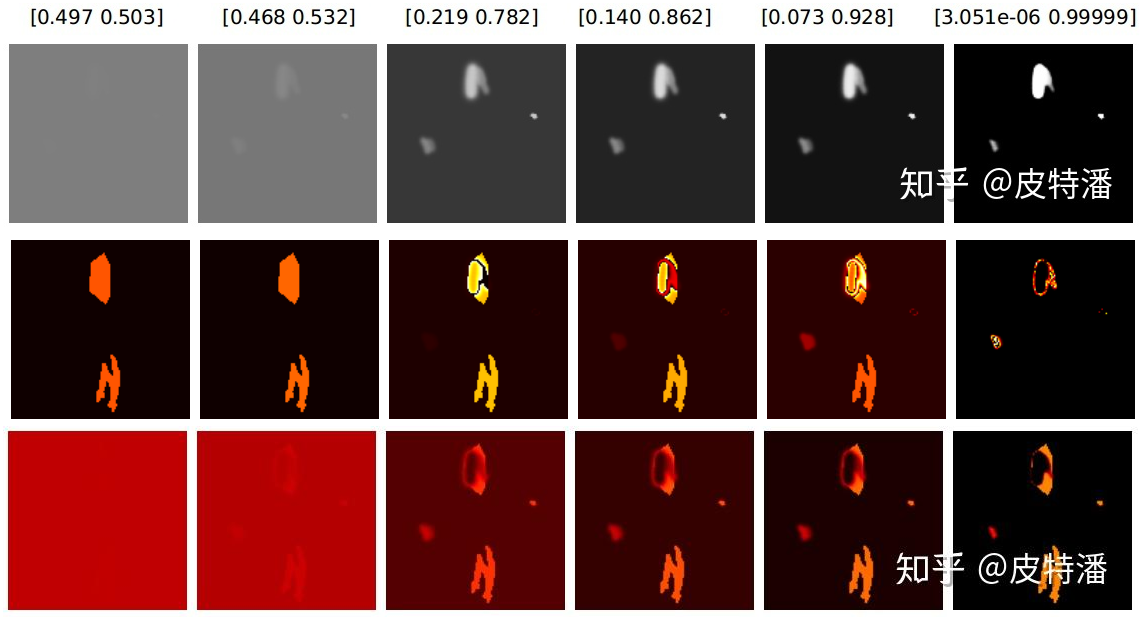
分析：1）当 t=0 时，同样在 x 的正常范围内， x 的梯度值接近 0；2）当 t=1 时， t 在0点附近存在一个峰值，此时 t 接近0.5。随着预测值 t 越接近1或0，梯度越小，出现梯度饱和的现象。下图上下行是不同的输出概率 heatmap 和梯度，可以看出，梯度一开始就集中在前景上，对背景有忽视作用

dice loss 和交叉熵的区别？

上图从上到下，分别是模型输出概率、dice loss 、ce loss 损失的梯度
正负样本处理：dice loss 、ce loss 均有背景梯度，但是，dice loss 正样本的梯度值相对于 ce loss，颜色更亮，值更大，尤其是刚开始网络预测接近0.5的时候，说明 dice loss 对挖掘正样本更加有优势。ce loss 会公平处理正负样本，当出现正样本占比较小时，就会被更多的负样本淹没
结合使用：极端情况下，网络预测接近0或1时，对应点梯度值极小，dice loss 存在梯度饱和现象。此时预测失败 (FN，FP)的情况很难扭转回来（因为错误的点不贡献梯度，所以网络很难扭转回来）。因此结合 ce loss 使用，比如: dice+ce loss，dice + focal loss 等

什么是负对数似然损失(NLLLoss)？

1）极大似然估计(MLE) 通过寻找一组参数，最大化观测值的概率，这是已知数据出现概率的连乘，然后求偏导得到的
2）为了把积变和，对连乘取对数
3）然后在前面加负号，使得最大似然值变为最小对数似然
对参数的不同假设，可以得到不同数据出现的概率，也出现不同的负对数似然函数，如：高斯负对数似然损失、Poisson 负对数似然损失

什么是泊松负对数似然损失(PoissonNLLLoss)？

真实标签服从泊松分布的负对数似然损失，神经网络的输出作为泊松分布的参数λ
对于包含N个样本的batch数据 D( x , y )，x是预测标签，y是真实类别标签，服从泊松分布。x与y的维度相同
$\mathrm{P}(\mathrm{Y}=\mathrm{k})=\frac{\lambda^{\mathrm{k}}}{\mathrm{k} !} \mathrm{e}^{-\lambda}$
若x是神经网络的输出，且未进行归一化和对数化处理。第n个样本对应的损失ln为：
$\begin{aligned} \mathrm{P}\left(\mathrm{Y}=\mathrm{y}_{\mathrm{n}}\right)=\frac{x_{\mathrm{n}}^{\mathrm{y}_{\mathrm{n}}}}{\mathrm{y}_{\mathrm{n}} !} \mathrm{e}^{-\mathrm{x}_{\mathrm{n}}} \\ 1_{\mathrm{n}}=-\log \mathrm{P}\left(\mathrm{Y}=\mathrm{y}_{\mathrm{n}}\right)=\mathrm{x}_{\mathrm{n}}-\mathrm{y}_{\mathrm{n}} \log \mathrm{x}_{\mathrm{n}}+\log \left(\mathrm{y}_{\mathrm{n}} !\right) \end{aligned}$

什么是高斯数似然损失(GaussianNLLLoss)？

真实标签服从高斯分布的负对数似然损失，神经网络的输出作为高斯分布的均值和方差
对于包含N个样本的batch数据D(x,var,y)，x神经网络的输出，作为高斯分布的均值，var神经网络的输出，作为高斯分布的方差，y是样本对应的标签，服从高斯分布。x与y的维度相同，var和x的维度相同
第n个样本对应的损失ln为 $l_{n}=0.5 *\left(\log \left(\max \left(\operatorname{var}_{\mathrm{n}}, \mathrm{eps}\right)\right)+\frac{\left(\mathrm{x}_{\mathrm{n}}-\mathrm{y}_{\mathrm{n}}\right)}{\max \left(\operatorname{var}_{\mathrm{n}}, \mathrm{eps}\right)}\right)$

什么是MarginRankingLoss ？

计算输入input，other 和标签label间的 margin rank loss 损失 $margin\_rank\_loss = max(0, -label * (input - other) + margin)$

什么是MultiLabelMarginLoss？

对于mini-batch(小批量) 中的每个样本

什么是SoftMarginLoss？

$\mathrm{loss}(x,y) = \sum_i \dfrac{\log(1 + \exp (-y[i] \cdot x[i]))}{x.\mathrm{nelement()}}$
$x.\mathrm{nelement()}$ 为输入x中的样本个数。注意这里y也有1和-1两种模式

什么是MultiLabelSoftMarginLoss？

多标签 one-versus-all 损失

什么是HingeEmbeddingLoss？

测量输入张量的损耗x 和一个标签张量y （包含1或-1）。通常用于测量两个输入是否相似或不相似，例如使用L1成对距离作为x ，通常用于学习非线性嵌入或半监督学习 $l_{n}= \begin{cases}x_{n}, & \text { if } y_{n}=1 \\ \max \left\{0, \Delta-x_{n}\right\}, & \text { if } y_{n}=-1\end{cases}$

什么是CosineEmbeddingLoss？

$\operatorname{loss}(x, y)=\left\{\begin{array}{ll} 1-\cos \left(x_{1}, x_{2}\right), & \text { if } y==1 \\ \max \left(0, \cos \left(x_{1}, x_{2}\right)-\operatorname{margin}\right), & \text { if } y==-1 \end{array}\right.$

什么是三元损失TripletMarginLoss？

就构成了一个三元组，学习目标是让Positive和Anchor之间的距离 D ( a , p )尽可能的小，Negative和Anchor之间的距离 D ( a , n )尽可能的大 $L=\sum_{i}^{N}\left[\left\|f\left(x_{i}^{a}\right)-f\left(x_{i}^{p}\right)\right\|_{2}^{2}-\left\|f\left(x_{i}^{a}\right)-f\left(x_{i}^{n}\right)\right\|_{2}^{2}+\alpha\right]_{+}$

什么是CTCLoss？

连接时序分类损失，可以对没有对齐的数据进行自动对齐，主要用在没有事先对齐的序列化数据训练上。比如语音识别、ocr识别等等

什么是0-1损失？

计算 0-1 分类损失的总和或平均值
$L(Y, f(x)) = \begin{cases} 1,& Y\ne f(x)\\ 0,& Y = f(x) \end{cases}$
当且仅当预测为真的时候取值为1，否则取值为0。该损失函数能够直观的刻画分类的错误率，但是由于其非凸、非光滑的特点，使得算法很难直接对该函数进行优化
1
2
3
4
5
6
7
>>> from sklearn.metrics import zero_one_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> zero_one_loss(y_true, y_pred)
0.25
>>> zero_one_loss(y_true, y_pred, normalize=False)
1

逻辑斯谛损失 (Logistic Loss)？

又称对数损失
$L(\hat y,y)=-(ylog(\hat y)+(1-y)log(1-\hat y))$
Logistic损失函数也是0-1损失函数的凸上界，且该函数处处光滑，因此可以使用梯度下降法进行优化。但是，该函数对所有样本点都做惩罚，因此对异常点更为敏感
1
2
3
4
5
>>> from sklearn.metrics import log_loss
>>> y_true = [0, 0, 1, 1]
>>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
>>> log_loss(y_true, y_pred)
0.1738...

什么是指数损失 (Exponential Loss)？

指数损失函数对于预测模型输出的符号与类别标签的符号不一致的情况有强烈的惩罚，相反，当二者符号一致且乘积数值较大时，损失函数的取值会非常小， AdaBoost就是以指数损失函数为损失函数 $L(Y, f(x)) = \exp(-Yf(x))$

什么是对数损失(Logarithmic Loss)?

又称二元交叉熵损失，主要用于逻辑回归算法（Logistric Regression）
$loss=-\frac {1} {N} \sum_{i=1}^My_{ij}log(p_{ij})$
这里N是样本的数量，M是类别数量，yij和pij都是二值型标志位，表示第i个样本是否属于第j类，y表示真实值，p表示预测值。logloss越小说明算法越好。在实际编程应用中注意添加一个冗余项(1e−15)之类的，避免出现log0这样的情况

对数损失函数和极大似然估计有什么关系？

对数损失函数等价于极大似然估计(MLE)
似然估计：一组参数在一堆数据下的似然值，等于每一条数据在这组参数下的条件概率之积
对数损失：而损失函数一般是每条数据的损失之和，为了把积变为和，就取了对数
对数损失加负号：让最大似然值和最小损失对应起来

什么是合页损失(铰链损失) (Hinge Loss)?

也称为铰链损失，用于分类的损失函数，旨在找到距离每个训练样本都尽可能远的决策边界(decisionboundary)，从而使样本和边界之间的裕度最大化，即最大间隔算法。其中 $y_i(wx_i+b)$ 为点 $x_i$ 到超平面(w,b)的函数间隔
$\left\{ \begin{aligned} sample_{pos}:w*x_i+b>=1 \\ sample_{neg}:w*x_i+b<=-1 \end{aligned} \right. \Rightarrow y_i(wx_i+b)>=1 \\ \underset{\min}{w,b}\sum_{i=1}^N (1-y_i(wx_i+b))+\lambda\Vert w\Vert ^2$

由于Hinge损失在 $y_i(w*x_i+b)$ 处不可导，因此不能使用梯度下降算法优化，而是使用次梯度下降法

>>> from sklearn import svm
>>> from sklearn.metrics import hinge_loss
>>> X = [[0], [1]]
>>> y = [-1, 1]
>>> est = svm.LinearSVC(random_state=0)
>>> est.fit(X, y)
LinearSVC(random_state=0)
>>> pred_decision = est.decision_function([[-2], [3], [0.5]])
>>> pred_decision
array([-2.18...,  2.36...,  0.09...])
>>> hinge_loss([-1, 1, 1], pred_decision)
0.3...

什么是修正huber损失?

如果 $y_i f(x_i) > 1$ ，则 $L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))^2$ ,否则， $L(y_i, f(x_i)) = -4 y_i f(x_i)$

什么是Brier损失(Brier score loss)?

计算二分类的Brier分数
$BS = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1}(y_i - p_i)^2$

Brier score loss也在0到1之间，值越低（均方差越小），预测越准确

>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.4])
>>> y_pred = np.array([0, 1, 1, 0])
>>> brier_score_loss(y_true, y_prob) #((0-0.1)^2+(1-0.9)^2+(1-0.8)^2+(0-0.4))/2
0.055 
>>> brier_score_loss(y_true, 1 - y_prob, pos_label=0)
0.055
>>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham")
0.055
>>> brier_score_loss(y_true, y_prob > 0.5)
0.0

什么是标签排名损失(label rank loss)?

该损失对样本中错误排序的标签对的数量进行平均，即真实标签的分数低于虚假标签，加权为虚假标签和真实标签的有序对数量的倒数

>>> import numpy as np
>>> from sklearn.metrics import label_ranking_loss
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_loss(y_true, y_score)
0.75...
>>> # With the following prediction, we have perfect and minimal loss
>>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]])
>>> label_ranking_loss(y_true, y_score)
0.0

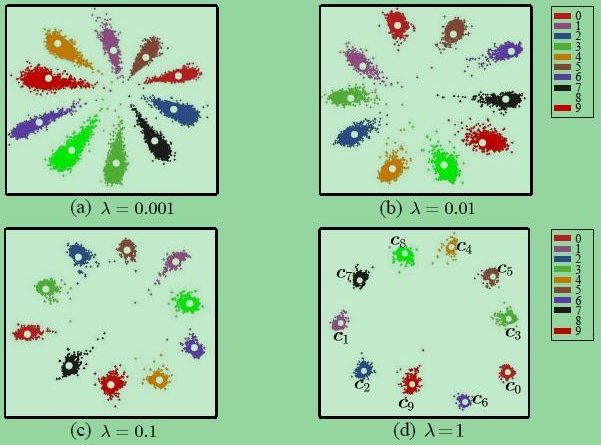
什么是内聚外斥损失(Center Loss) ？

在分类任务中， Cross Entropy Loss (交叉熵代价) + Softmax 组合被广泛应用，可以理解为：更相似(同类/同物体)的图像在特征域中拥有“更近的距离”, 相反则”距离更远“，Softmax损失能够要求特征具有类间的可分离性，但不能约束特征的类内紧凑性，因此Center Loss被提出解决这个问题
计算公式
$L = L_{S} + \lambda L_{C} \\ = -\sum^{m}_{i=1}log\frac{e^{W_{y}^{T}x_{i}+b_{y_{i}}}}{\sum^{m}_{i=1}e^{W^{T}_{j}x_{i}+b_{j}}} + \frac{\lambda}{2}\sum^{m}_{i=1}||x_{i}-c_{y_{i}}||^{2}_{2}$
如图是softmax加center Loss前后的效果，可以看出，类间距离变大了，类内距离减少了

什么是IOU loss?

目标检测算法检测评价使用 IoU，但实际回归的是坐标框4个坐标点，两者是不等价的，甚至绝对值损失 (L1Loss)或者平方损失 (MSELoss/L2Loss)相等时，其 IoU 不是唯一的。旷视2016年提出 IoU Loss，其将4个点构成的 box 看成一个整体进行回归 (以下2种定义均可) $$\begin{array}{ll}Loss_{IOU}=-\ln (IOU) \ Loss_{IOU}=1-IOU\end{array}$$
缺点： 当预测框和真实框的 IOU>0时，其 loss 可以被算出来，但是对于哪些 IOU=0的框，无法算出 loss。导致无法区分哪些预测更加靠近真实框的结果

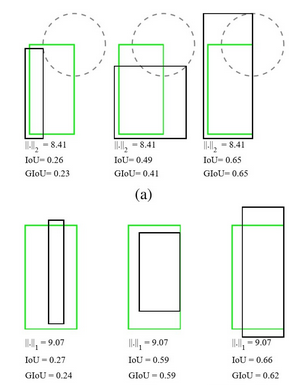
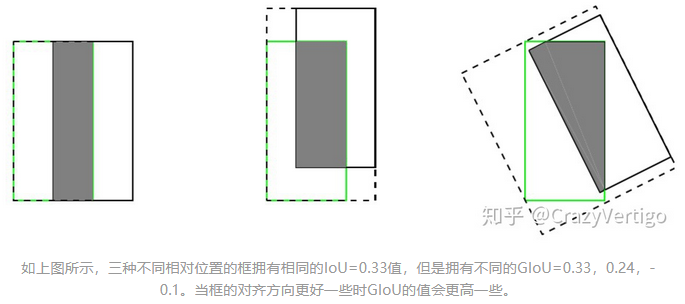
什么是GIOU loss?

考虑到IOU loss存在个问题：（1）无法对两个不重叠的框进行优化；（2）无法反映出两个框到底距离有多远。IoU Loss引入了C检测框（包含真实框和检测框的最小矩形），当检测框与真实框有重叠时，GIoU等效于IOU
$Loss_{GIOU}=1-(IOU-\frac{C-(A \bigcup B)}{C})$
缺点： 当目标框完全包裹预测框的时候，IoU 和 GIoU 的值都一样，此时 GIoU 退化为 IoU, 无法区分其相对位置关系

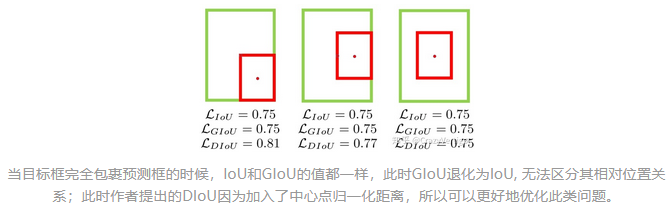
什么是 DIOU Loss?

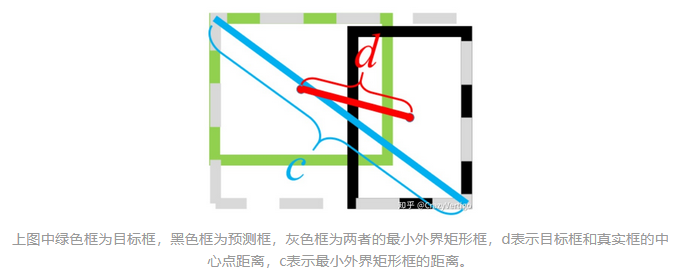
当目标框完全包裹预测框的时候，IOU loss和GIoU loss的值都一样，此时GIoU退化为IoU, 无法区分其相对位置关系，此时作者提出的DIoU因为加入了中心点归一化距离
$L_{DIoU}=1-IoU+\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}$
$b, b^{gt}$ 表示预测框和真实框中心点， $\rho$ 表示欧式距离， $c$ 表示预测框与真实框的最小外接矩形的对角线距离

什么是 CIOU loss？

在 DIou Loss 的惩罚项基础上加了一个影响因子 $\alpha v$ ，这个因子把预测框长宽比拟合目标框的长宽比考虑进去
$L_{CIoU}=1-IoU+\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}+\alpha v\\$
$b,b^{gt}$ 表示预测框和真实框中心点， $\rho$ 表示欧式距离， $c$ 表示预测框与真实框的最小外接矩形的对角线距离
$\alpha$ 是用于做权重参数， $v$ 是用来衡量长宽比一致性的参数
$\alpha=\frac{v}{(1-I o U)+v}\\ v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2}$

什么是 EIOU loss?

CIoU loss同时考虑到回归框宽高比例以及真实框与预测框中心距离，但是存在一个问题，他仅仅将宽高比例作为影响因子，如果说有两个框中心点与原始图保持一致，宽高比例相同但是宽高的值不同，按照CIOUloss损失可能一致与回归目标不相符
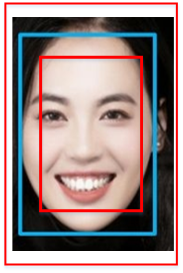
EIOU loss将原始的宽高比例，改为宽高值回归，将红色框的宽度与真实（蓝色）宽度进行损失，红色长度与真实长度进行回归
$=1-I O U+\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{\mathbf{g t}}\right)}{c^{2}}+\frac{\rho^{2}\left(w, w^{g t}\right)}{C_{w}^{2}}+\frac{\rho^{2}\left(h, h^{g t}\right)}{C_{h}^{2}}$
$b,b^{gt}$ 表示预测框和真实框中心点， $\rho$ 表示欧式距离， $c$ 表示预测框与真实框的最小外接矩形的对角线距离
$w,h$ 为预测框的宽高， $w^{gt},h^{gt}$ 为真实框的宽高， $C_w,C_h$ 为外接框的宽高
考虑在一张图像中回归误差小的高质量锚框的数量远少于误差大的低质量样本，质量较差的样本会产生过大的梯度影响训练过程，使用IOU值对EIOU loss进行加权，得到Focal EIOU loss
$L_{\text {Focal-EIOU }}=I O U^{\gamma} L_{E I O U}$

什么是 SIOU loss?

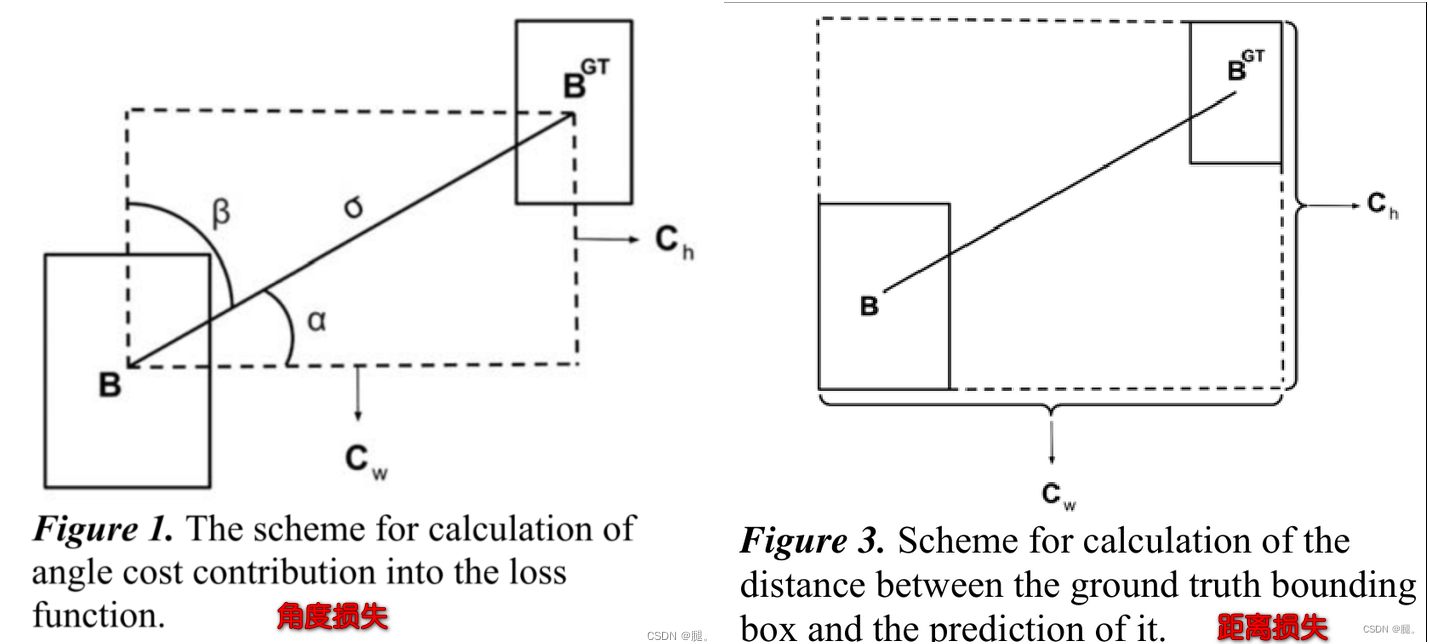
将预测框和真实框的角度考虑进来，加快收敛，下图B是目标框，B_GT是回归框，当B到B_GT的夹角小于alpha时，向最小alpha收敛，反之向beta收敛
SIoU =Distance cost（angle + distance）+Shape cost+IOU loss
角度损失 (angle loss):
$\begin{array}{c} \Lambda=1-2 * \sin ^{2}\left (\arcsin (x)-\frac{\pi}{4}\right) \\ \\ x=\frac{c_{h}}{\sigma}=\sin (\alpha) \\ \sigma=\sqrt{\left (b_{c_{x}}^{g t}-b_{c_{x}}\right)^{2}+\left (b_{c_{y}}^{g t}-b_{c_{y}}\right)^{2}} \\ c_{h}=\max \left (b_{c_{y}}^{g t}, b_{c_{y}}\right)-\min \left (b_{c_{y}}^{g t} b_{c_{y}}\right) \end{array}$
距离损失(Distance loss)：将角度信息考虑进行距离损失，当角度为0时，r=2，退化为距离损失
$\Delta=\sum_{t=x, y}\left(1-e^{-\gamma \rho_{t}}\right) \\ \\ \rho_{x}=\left(\frac{b_{c_{x}}^{g t}-b_{c_{x}}}{c_{w}}\right)^{2}, \rho_{y}=\left(\frac{b_{c_{y}}^{g t}-b_{c_{y}}}{c_{h}}\right)^{2}, \gamma=2-\Lambda$
形状损失(Shape loss)：θ为控制参数，如果θ值设置为1，将立刻优化形状，从而影响形状的自由运动
$\Omega=\sum_{t=w, h}\left(1-e^{-\omega_{t}}\right)^{\theta} \\ \\ \omega_{w}=\frac{\left|w-w^{g t}\right|}{\max \left(w, w^{gt}\right)}, \omega_{h}=\frac{\left|h-h^{g t}\right|}{\max \left(h, h^{g t}\right)}$
IOU损失(iou loss)： $1-IOU$
总损失(SIOU loss)： $L_{b o x}=1-IoU+\frac{\Delta+\Omega}{2}$

什么是标签平滑(Class label smoothing)?

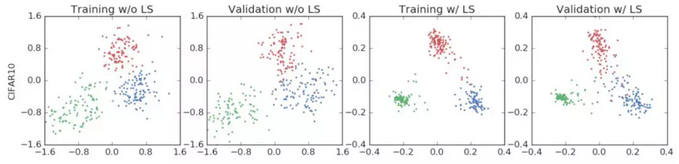
后面两列展示，标签平滑为最终的激活产生了更紧密的聚类和更大的类别间的分离
对于分类问题，特别是多分类问题，常常把向量转换成独热编码（one-hot encoding），对于损失函数，我们需要用预测概率去拟合真实概率，由此带来2个问题：（1）无法保证模型的泛化能力，容易造成过拟合；（2）全概率和0概率鼓励所属类别和其他类别之间的差距尽可能加大，而由梯度有界可知
对预测有信心可能表明模型是在记忆数据，而不是在学习， 平滑就是一定程度缩 label 中 min 和 max 的差距，适当让 label 两端的极值往中间靠，可以增加泛化性能

标签平滑(Class label smoothing) 的原理？

标签平滑(Class label smoothing) 目标是重构one-hot变量，平滑公式如下，其中为平滑后的标签向量，为平滑因子，为人为引入的固定分布
$y^{\prime}=(1-\epsilon) * y+\epsilon * u$
假设样本的 one-hot 化后的标签为[ 0 , 0 , 0 , 1 , 0 ]，仍假设我们已经得到了该样本进行 softmax 的概率矩阵 $p=\left[p_{1}, p_{2}, p_{3}, p_{4}, p_{5}\right]=[0.1,0.1,0.1,0.36,0.34]$ ，如果平滑因子
$\begin{array}{l} y_{1}=(1-\epsilon) *[0,0,0,1,0]=[0,0,0,0.9,0] \\ y_{2}=\epsilon *[1,1,1,1,1]=[0.1,0.1,0.1,0.1,0.1] \\ y=y_{1}+y_{2}=[0.1,0.1,0.1,1.0,0.1] \end{array}$

不使用标签平滑及使用标签平滑的损失如下计算交叉熵损失(CrossEntropyLoss) ，经过平滑后的损失变大，因为考虑了0位置的损失

\operatorname{loss}=-y * \log p=-[0,0,0,1,0] * \log ([0.1,0.1,0.1,0.36,0.34])=1.47 \\ \operatorname{loss_{smooth}}=-y * \log p=-[0.1,0.1,0.1,1.0,0.1] * \log ([0.1,0.1,0.1,0.36,0.34])=2.63

class CrossEntropyLossWithLabelSmoothing(nn.Module):
    def __init__(self, n_dim, ls_=0.9, reduction='mean'):
        super().__init__()
        self.n_dim = n_dim
        self.ls_ = ls_
        self.reduction=reduction
    def forward(self, x, target):
        target = F.one_hot(target, self.n_dim).float()
        target *= self.ls_
        target += (1 - self.ls_) / self.n_dim
        logprobs = torch.nn.functional.log_softmax(x, dim=-1)
        loss = -logprobs * target
        loss = loss.sum(-1)
        if self.reduction=='none':
            return loss
        elif self.reduction=='sum':
            return loss.sum()
        elif self.reduction=='mean':
            return loss.mean()
        else:
            raise ValueError('unrecognized option, expect reduction to be one of none, mean, sum')

参考：